入試数学コンテスト第2回第4問解答解説

$$\mathrm{OA} = \mathrm{AB} - \mathrm{OB} = 2 - r$$

である。

点 $\mathrm{A}$ は $x = 1$ 上の点であるから

$$(2 - r) \cos t = 1$$

したがって

$$r = 2 - \dfrac{1}{\cos t}$$

$- \dfrac{\pi}{2} \leqq t \leqq \dfrac{\pi}{2}$ のもとで, $r \geqq 0$ より

$$\begin{aligned} & r = 2 - \dfrac{1}{\cos t} \geqq 0 \\ & \iff \cos t \geqq \dfrac{1}{2} \\ & \iff - \dfrac{\pi}{3} \leqq t \leqq \dfrac{\pi}{3} \quad\cdots\cdots (1) \end{aligned}$$

点 $\mathrm{B}$ の座標を $(x,y)$ と置くと $$\begin{cases} x = -r \cos t = 1 - 2 \cos t \\ y = -r \sin t = \tan t - 2 \sin t \end{cases}$$

$t$ が 範囲（1）を動くとき, $y = \tan t - 2 \sin t$ の軌跡は $x$ 軸に関して対称である。

$y$ の最大値を考えたいので, $y$ が $y \geqq 0$ の領域を動くような $t$ の範囲

$$- \dfrac{\pi}{3} \leqq t \leqq 0 \quad\cdots\cdots (2)$$

について考えれば十分である。

$$\begin{aligned} & \dfrac{dy}{dt} = \dfrac{1}{\cos^2 t} - 2 \cos t = 0 \\ & \iff \cos t = \left(\dfrac{1}{2}\right)^{\frac{1}{3}} \quad\cdots\cdots (3) \end{aligned}$$

である。

$\dfrac{1}{2} < \left(\dfrac{1}{2}\right)^{\frac{1}{3}} < 1$　に注意すると, 範囲（2）には式（3）を満たす実数 $t$ がただ一つ存在する。この $t$ を $t_0$ とする。

これらに注意すると $y$ の増減表は以下のようになる。

$$\begin{array}{c|ccc} t & - \dfrac{\pi}{3} & \cdots & t_0 & \cdots & 0 \\ \hline \dfrac{dy}{dt} & & + & 0 & - \\ \hline y & 0 & \nearrow & y_{\text{max}} & \searrow & 0 \end{array}$$

$y$ 座標は $t = t_0$ で最大値 $y_{\text{max}}$ をとる。

式（3）より

$$\sin t_0 = - \sqrt{1 - \left(\dfrac{1}{2}\right)^{\frac{2}{3}}} \\ \tan t_0 = - \sqrt{2^{\frac{2}{3}} - 1}$$

である。

$2^{\frac{2}{3}} - 1　= X$ と置くと,

$$\sin t_0 = - \sqrt{\dfrac{X}{X + 1}} \\ \tan t_0 = - \sqrt{X}$$

であり,

$$\begin{aligned} y_{\text{max}} &= \tan t_0 - 2 \sin t_0 \\ &= - \sqrt{X} + 2 \sqrt{\dfrac{X}{X + 1}} \\ &= \sqrt{X} \left(-1 + \sqrt{\dfrac{4}{X + 1}} \right) \\ &= \sqrt{X} \left(-1 + 2^{\frac{2}{3}} \right) \\ &= \sqrt{2^{\frac{2}{3}} - 1} \left(2^{\frac{1}{3}} + 1 \right)\left(2^{\frac{1}{3}} - 1 \right) \\ &= \sqrt{\left(2^{\frac{2}{3}} - 1\right)\left(2^{\frac{1}{3}} + 1 \right)^2} \left(2^{\frac{1}{3}} - 1 \right) \end{aligned}$$

となる。平方根の内部を整理すると

$$\begin{aligned} & \left(2^{\frac{2}{3}} - 1\right)\left(2^{\frac{1}{3}} + 1 \right)^2 \\ &= \left(2^{\frac{2}{3}} - 1\right)\left(2^{\frac{2}{3}} + 2^{\frac{4}{3}} + 1 \right) \\ &= 2^{\frac{4}{3}} + 2^{\frac{6}{3}} + 2^{\frac{2}{3}} - 2^{\frac{2}{3}} - 2^{\frac{4}{3}} - 1 \\ &= 3 \end{aligned}$$

であるから,

$$y_{\text{max}} = \sqrt{3} \left(\sqrt[3]{2} - 1 \right)$$

曲線 $C$ を図示すると下図のようになる。

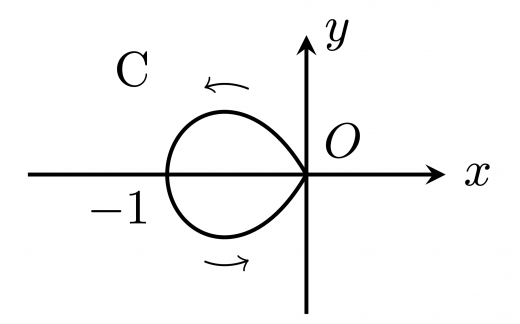
曲線 $C$ の $x$ 軸に関する対称性から, 範囲（２）のもとで考える。

範囲（２）において $x$ の増減表は以下の通りになる。

$$x = 1 - 2 \cos t$$

$$\dfrac{dx}{dt} = 2 \sin t$$

$$\begin{array}{c|ccc} t & - \dfrac{\pi}{3} & \cdots & 0 \\ \hline \dfrac{dx}{dt} & - & - & 0 \\ \hline x & 0 & \gets & -1 \end{array}$$

したがって, 求める面積を $S$ とするとき

$$\begin{aligned} \dfrac{S}{2} &= \int_{- 1}^0 y \, dx \\ &= \int_{0}^{- \frac{\pi}{3}} y \, \dfrac{dx}{dt} dt \\ &= \int_{0}^{- \frac{\pi}{3}} \left(\tan t - 2 \sin t\right) \cdot 2 \sin t \, dt \\ &= 2 \int_{0}^{- \frac{\pi}{3}} \left(\dfrac{\sin^2 t}{\cos t} - 2 \sin^2 t\right) \, dt \\ &= 2 \int_{0}^{- \frac{\pi}{3}} \left(\dfrac{1 - \cos^2 t}{\cos t} - 1 + \cos 2t \right) \, dt \\ &= 2 \int_{0}^{- \frac{\pi}{3}} \left(\dfrac{1}{\cos t} -\cos t - 1 + \cos 2t \right) \, dt \\ &= 2 \int_{0}^{\frac{\pi}{3}} \left(- \dfrac{1}{\cos t} + \cos t + 1 - \cos 2t \right) \, dt \end{aligned}$$

である。

第一項について

$$\begin{aligned} I_1 &= \int_{0}^{\frac{\pi}{3}} \dfrac{1}{\cos t} \, dt \\ &= \int_{0}^{\frac{\pi}{3}} \dfrac{\cos t}{(1 + \sin t)(1 - \sin t)} \, dt \\ &= \dfrac{1}{2} \int_{0}^{\frac{\pi}{3}} \left(\dfrac{\cos t}{1 + \sin t} + \dfrac{\cos t}{1 - \sin t} \right) \, dt \\ &= \dfrac{1}{2} \left[\log \left| \dfrac{1 + \sin t}{1 - \sin t} \right| \right]_{0}^{\frac{\pi}{3}} \\ &= \dfrac{1}{2} \log \dfrac{2 + \sqrt{3}}{2 - \sqrt{3}} \\ &= \log (2 + \sqrt{3}) \end{aligned}$$

である。

第二項以降について

$$\begin{aligned} I_2 &= \int_{0}^{\frac{\pi}{3}} \left(\cos t + 1 - \cos 2t \right) \, dt \\ &= \left[\sin t + t - \dfrac{1}{2} \sin 2t \right]_{0}^{\frac{\pi}{3}} \\ &= \dfrac{\sqrt{3}}{2} + \dfrac{\pi}{3} - \dfrac{\sqrt{3}}{4} \\ &= \dfrac{\sqrt{3}}{4} + \dfrac{\pi}{3} \end{aligned}$$

である。以上から

$$\begin{aligned} \dfrac{S}{2} &= 2 (-I_1 + I_2) \\ \iff S &= 4 (-I_1 + I_2) \\ &= -4 \log (2 + \sqrt{3}) + \sqrt{3} + \dfrac{4 \pi}{3} \end{aligned}$$