東大理系数学2017入試過去問解答解説
※以下の解答と解説は東京大学が公表したものではなく,当サイトオリジナルのものです。問題は東京大学第2次試験問題からの引用です。
この記事では,東京大学の2017年度入学試験の理系数学について解説します。
第一問 [三角関数,関数の最大値]
第一問 [三角関数,関数の最大値]
実数 に対して
とし, で定義された関数
を考える。
と を の整式で表せ。
が の範囲で最小値 をとるための についての条件を求めよ。また,条件をみたす点 が描く図形を座標平面上に図示せよ。
まず は の中身が と様々な値をとるので,それらを で統一していきましょう。
3倍角,倍角の公式を使うと一発です。→三角関数の基本公式一覧
三角関数の公式は覚えるのも大事ですが,全て加法定理から導けますので,いざというときのために自力で導出できるようにしておきましょう。
より,
また, なので,( より, とあわせて)
を求めるときに,問題文に整式と書いてあることから割りきれることが期待できます。
また, とおくと, として の整式になります。 より, ですが,仮に となる場合を考えると, ですね。ここからも整式 は を因数に持つことがわかります。
次に です。1変数関数の最大最小は微分をして増減を調べれば求められます。
今回, は の2次式なので,平方完成でも挙動がわかりますね。
ここで, の定義域が全実数でないことを忘れないようにしましょう。 の変域や の条件から範囲が絞れますね。
を で表しているので,文字消去と考えられます。文字消去をしたときにはその文字の変域や条件を移すことを意識しましょう。
より, となり,この範囲で の最小値が になる条件を考える。
とおくと,
(ⅰ) のとき,また, のとき
グラフの概形は下図太線部(○は含まず)のようになり最小値は存在せず,条件を満たさない。

(ⅱ) のとき
のグラフの概形は下図太線部(○は含まず)のようになる。

よって最小値は, であり,これが になる条件を考えるので,
よって,求める条件は で をみたすことで,下図太線部(○は含まず)ようになる。

放物線の軸と の定義域との関係で場合わけができますね。
不等式を書く際には「」の場合を含むかどうかを意識しましょう。
第二問 [確率]
第二問 [確率]
座標平面上で 座標と 座標がいずれも整数である点を格子点という。格子点上を次の規則に従って動く点 を考える
最初に,点 は原点 にある。
ある時刻で点 が格子点 にあるとき,その 秒後の点 の位置は,隣接する格子点 ,,, のいずれかであり,また,これらの点に移動する確率は,それぞれ である。
点 が,最初から 秒後に直線 上にある確率を求めよ。
点 が,最初から 秒後に原点 にある確率を求めよ。
上という条件をどのように処理するかがカギになるでしょう。 これは 座標と 座標の差が 」とみなせます。よって,その差が 秒毎にどのように変化するか考えれば答えを導けます。
この方法が思いつかない場合は,実際に点の移動を座標平面上に書いて考えてみましょう。最初の移動によって, 上から か のいずれかの上にそれぞれ の確率で移動することがわかりますね。

最初は 上なので 秒の間に 回ずつ 切片が増減すれば 秒後に 上に来ることがわかります。
秒後の点 は 上にあるが, 秒後に に移動すると, 上に, に移動すると, 上に移動する。
つまり, 秒たつと ずつの確率で,点 を通り傾きが の直線の 切片が 増減することがわかる。
ここで,最初に点 は 上にあって, 切片は である。 秒後に点 を通る傾き の直線の 切片が であるのは, 切片は に 回, に 回移動する場合である。
よって,求める確率は
を誘導と考えて を解くエレガントな解法は以下のようになります(普通の解法も下に書いてあります)。
秒後の点 は 上にあるが, 秒後に に移動すると, 上に, に移動すると, 上に移動する。
よって 秒後に 上に点 がある確率は と同様に考えて,
ここで, 回移動することによる点 を通る傾き の直線の 切片の変化量を とおく。
で となる確率を表すとして,
となる。
また,点 から へ移動する確率は なので,
となり,
が成立するので,点 を通る傾き の直線の 切片の変化は独立である。
これと,点 が原点 上にある条件が, 上でかつ 上にある条件と等しいことから,求める確率は より
上にある確率の 乗に等しくなっていますね。原点 上にあるという条件を 上かつ 上と読み替えて,それぞれの確率をかけることで答えを求めています。
これは 上にある確率と 上にある確率が独立な場合に成立することですので,その点をきちんと証明してから使いましょう。
その証拠に という確率を掛け合っても,原点 上にある確率にならないですね。確率の独立について詳しくは以下に書いてあります。→独立と無相関の意味と違いについて
この解法を考えつくことは難しいでしょうが,この機会に確率の独立について今一度確認しましょう。
次に,現実的な解法です。
6秒後に点 が 上にあるためにはどのように動くかを具体的に考えてみましょう。
や, といった動き方が考えられます。
ここから左と右に同じ回数,上と下に同じ回数動けばよいということがわかるでしょう。
最初に点 は原点上にあるため, 秒後に点 が原点にあるためには 座標が正負にそれぞれ同じ回数動けばよい。
よって,動き方の組み合わせは以下のようになる。
それぞれの移動の確率は なので,
の確率は,
の確率は,
以上より,求める確率は
第三問 [複素数]
第三問 [複素数]
複素数平面上の原点以外の点 に対して, とする。
を でない複素数とし,点 と原点 を結ぶ線分の垂直二等分線を とする。点 が直線 上を動くとき,点 の軌跡は円から 点を除いたものになる。この円の中心と半径を求めよ。
の3乗根のうち,虚部が正であるものを とする。点 と点 を結ぶ線分上を が動くときの点 の軌跡を求め,複素数平面上に図示せよ。
複素数で という変換では は を中心が原点,半径が の円を反転円として反転した点になります。→反転幾何の基礎
, からわかりますね。
本問の変換は より,, となります。
これは反転した図形の偏角を 倍したもの。つまり,実軸対称に移動させた図形と分かります。
反転の知識を利用すると, が原点を通らない直線なので, は原点を通る円となることもわかった上で解けるでしょう。
また,ここまで詳しく分からずとも の条件を数式で表して, になおして円の方程式になるように変形すれば十分に解くことができます。
点 と原点の垂直二等分線 は点 と から等距離にある点の集合なので, となる。
ここで, より なので, としてよく,
よって, は中心が ,半径が の円上のうち, より,原点以外の点。
は反転の知識があれば(なくてもあまり複雑でない式変形をするだけで),円になることはわかるので,問題文で「円になる」ことに言及がないことも考えられます。
これを機に反転について理解し,問題で出たときには気付けるようにしましょう。
では線分に対して変換をするので を利用できそうです。 の直線 に対応する直線が何であるかを考えましょう。
より, は原点 と の垂直二等分線上にある。
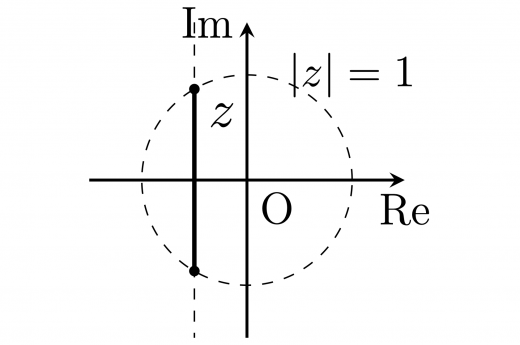
よって, より は中心 半径 の円周上にある。
また, を結んだ線分は であり, から となるので,
は中心 半径 の円周上のうち を満たす部分。

本問は と違い,直線ではなく線分上ということで,そこの処理をどうするかが問題です。
今回は が半径 の円の内側ということで, と分かりますね。図を書くと気づけるでしょう。
とおいて に代入しても解くことができます。
の条件を に移しましょう。
第四問 [数列,整数]
第四問 [数列,整数]
とおき,自然数 に対して
と定める。以下の問いに答えよ。ただし設問 は結論のみを書けばよい。
の値を求めよ。
とする。積 を, を用いて表せ。
は自然数であることを示せ。
と の最大公約数を求めよ。
文系の第四問と同じでした。誘導も丁寧で解きやすい問題です。
は計算するだけです。詳しくは,→分母の有理化や実数化について,→分母の有理化の方法と例題6問
も を計算してみるとわかります。
のとき
を解くときに で求めた を代入したくなるかもしれませんが,その場合 となってしまい, で表せません。
は直接示すのは難しそうです。全ての自然数に関する命題で,直接示すのが難しそうな場合は,帰納法が機能する場合が多いです。→数学的帰納法をわかりやすく【例題3問、応用5パターン】
帰納法を使うために必要なことはなんでしょうか。後ろの項(例えば )を前の項(例えば )を使って表すことですね。ここまで考えて, と繋げられると完璧です。
今回は を使って, を表せますね。
より, で
が成立する。
ここで, は自然数であることを数学的帰納法で示す。
のとき
より,自然数である。
で が自然数になると仮定する。
このとき, なので より,
が成立し,仮定より が自然数なので, が自然数になる。
つまり, で題意を満たすとき, でも題意をみたす。
以上 より,数学的帰納法で示された。
公約数に関する式変形で有名なものといえばユークリッドの互除法でしょう。→ユークリッドの互除法の証明と不定方程式
の式をよく見ると,互除法を有効に使えそうな形をしています。
自然数 の最大公約数を と表すことにする。
このとき, の範囲で を で割った商とあまりについて考えると,
- より が成立する
- 漸化式より
となるので,商は であまりは である。よって,ユークリッドの互除法より
となる。
よって, の範囲で は一定となる:
より, なので,求める最大公約数は
互除法なんて思いつかない!!という場合は, あたりの値を の式を使って計算してみるとよいでしょう。
となりますので,ここからどの隣り合う2数も最大公約数が と気付けると,互除法に近づけるのではないでしょうか。
第五問 [二次関数]
第五問 [二次関数]
を実数とし,座標平面上で次の つの放物線 の共通接線について考える。
直線 が共通接線であるとき, を用いて と を表せ。ただし とする。
傾き の共通接線が存在するように の値を定める。このとき,共通接線が 本存在することを示し,それらの傾きと 切片を求めよ。
方程式を眺めていても共通接線がどのようなものであるのか想像がつきにくいと思いますので,グラフを書いて考えていきましょう。
まず, はそれぞれ軸が と重なる放物線で, 対称になっていることが分かると思います。
その元でグラフを書くと以下のような場合が考えられるでしょう。

このイメージを持って解けると解きやすくなります。
方針としては に接する条件をそれぞれ数式化していくと良いでしょう。
共通接線 を とおき, と連立すると
これが重解を持つので, 判別式 が成立し,
次に, のとき, は 軸平行になるので と接さないので, としてよく, となるので, と連立して
これも重解を持つので, 判別式 が成立し,
以上 より, なので, に代入して
よって,
文字を含む式で割る時は 割る数 を確認してからにしましょう。
この式変形について,図形的な意味を考えてみます。
まず,今回の の式を変形するときの条件, の持つ意味についてです。
については,答案中でも書いてあるように, の式の解になり得ない,つまり,共通接線の傾きとして存在し得ないことがわかりますね。
についてはどうでしょうか。今回は問題文中で, とするという条件があるのであまり考えずに両辺からわってしまいましたが, の式は のとき必ず成立します。つまり,必ず の式の解になるのです。
これはどのような に対しても の傾きの共通接線が存在することを意味します。上に例で出した つの図からもわかりますね。
次に, についてです。 対称な図形であることを考えると, も同じ になるはずですが,実際に
となることからも での の値が等しいことが分かります。
このような図形的な意味を考えることで検算にもなりますので,是非参考にしてください。
では が与えられていますので, の値が求められますね。
と より,
これを に代入して,
これをみたす の組み合わせの が求める共通接線となる。
式 より となるので,式 に代入して
よって答えは
の に を代入して としてもいいですが,これでは を見逃してしまうでしょう。
これは の式より下では のもとで変形しているからです。
この解法で解いて の場合を別で考えても構いませんが,解答例のように解くのがきれいです。
また, を図示すると以下のようになります。

第六問 [回転体の体積]
第六問 [回転体の体積]
点 を原点とする座標空間内で,一辺の長さが の正三角形 を動かす。また,点 に対して, を とおく。ただし とする。
点 が 上にあるとき,点 の 座標がとりうる値の範囲と, がとりうる値の範囲を求めよ。
点 が平面 上を動くとき,辺 が通過しうる範囲を とする。 の体積を求めよ。
軸上 と に一辺がある正三角形の 軸上ではない頂点なので,図を書けば 上の円となるイメージはできるでしょう。
の最大最小は, が最大と最小のときというのは直感的にわかると思いますが,それを説明するには数式化した方が簡単です。
空間上の角を扱う際は幾何の定理の他に,ベクトルの内積を思いつけるようにしましょう。
とおくと,
となるので, の取りうる範囲を考える。
ここで は正三角形で, はそれぞれ なので,点 は下図のように,平面 上に中心 半径 の円周上を取りうる。
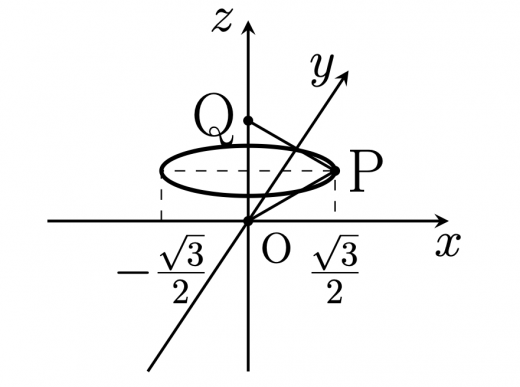
よって, となり, と合わせて,
として, から, の方程式を求めても構いません。
では, からどのように変わっているでしょうか。 の図形で,点 が 軸を中心に回転するので,全体が 軸を回転軸とした回転体になっています。
回転体の体積を求める図形では,回転軸に垂直な断面の断面積を考えて,それを回転軸方向に積分するのが定石です。→回転体の体積を求める公式
回転軸に垂直な断面の断面積を求めるには,回転軸に垂直な断面の回転前の形状を知ることが必要になります。そして,それには回転前の図形のイメージを持つとともに,方程式を求めると良いことが多々あります。
その際,別の断面を考えることも有効でしょう。本問では例えば回転前の 平面は以下のようになります。

ここから,回転前の の図形の方程式を求められます。
における の動く範囲は,上図の太線の円上の点と,点 とを結んだ図形。 はこれを 軸中心に回転させた図形となる。
回転前の の図形は, において, 軸から 離れた点の集合であり,
と表せる。
この図形の における断面の方程式は, となり,下図。

この図形と 軸との距離は近いところで ,遠いところで である。
軸中心に回転させると断面積は
となるので, が 平面対称であることと合わせて,体積は
における断面図, は双曲線になります。→双曲線の漸近線の簡単な求め方と証明
回転前の図形が円錐の側面になっていること,円錐を母線より急に切ると双曲線ができることからもわかるでしょう。→二次曲線の分類(四通りの方法)
本問では点 を固定して を動かしてから点 を動かすような誘導になっています。
誘導がなかった場合でも, に対する の位置を固定して を動かす場合と,点 を固定して を動かす場合を比較して解きやすい形を考えるようにしましょう。
東大理系数学2017入試過去問解説まとめ
東大理系数学2017入試過去問解説まとめ
全体として近年の東大の理系数学の中では簡単な問題が多い年でした。理科三類の受験生や数学を得点源にしたい受験生は 点は取れるとよいでしょう。
各問題についてです。
第一問は三角関数も二次関数冷静に対処すれば問題なくこなせたと思います。
第二問の確率は,図を書くとわかりやすかったでしょう。 秒しかないので最悪書き出していくことも十分に可能です。きれいな解き方が思いつかなくても自分でうまく一般化すれば十分完答できるのではないでしょうか。
第三問の複素数は,複素数に対して苦手意識を持っている人でも基本的な円の公式がわかれば解けたと思います。 はきれいに前の問題を利用できる問題でしたね。
第四問は数列です。文系でも同じ問題が出題されていましたが,整数に苦手意識があっても誘導にのれば解けたでしょう。
第五問の二次関数は少し骨があったでしょうか。見慣れない数式でも放物線なので,ビビる必要はありません。グラフを書くなどして冷静に対処しましょう。 また,数式の図形的な意味や 対称を利用した検算など図形と数式を結びつけながら問題を解けると数学を楽しめるようになるでしょう。
第六問は回転体でしたが, は難しかったでしょう。軸に垂直な断面を考えて,それを回転させた面積を積分するという典型的な解き方に落とし込むのが大事でした。
合格には高得点が必須の試験でした。数学を捨てていた受験生にはむしろ厳しい年だったと言えそうです。









