三角関数の基本公式一覧
三角関数の基本的な公式を一覧にしました。青枠内の公式がすべて理解できているか,確認してみてください。
そもそも三角関数とは
そもそも三角関数とは
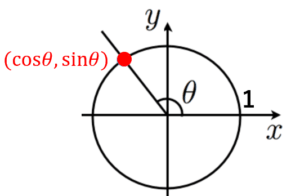
三角関数とは,以下で定義される のことです。
-
とは,単位円上の角度 に対応する点の 座標
-
とは,単位円上の角度 に対応する点の 座標
-
とは, のこと
詳しい説明: 三角関数の3通りの定義とメリットデメリット
三角関数の計算力を上げたい方は,最短で得点力を上げる!高校数学の問題集〈典型250問〉も参考にしてください。
三角関数の相互関係
三角関数の相互関係
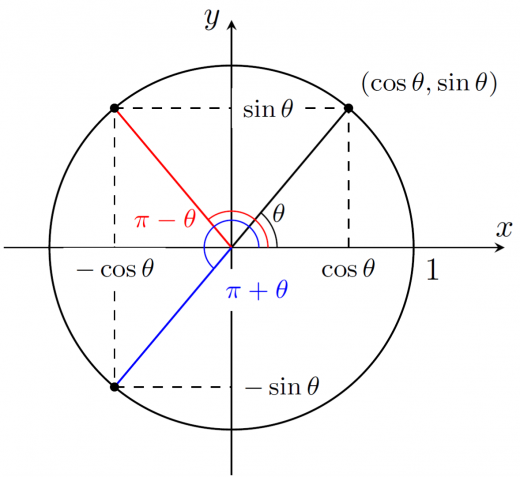
余角・補角・負角の公式
余角・補角・負角の公式
三角関数の加法定理
三角関数の加法定理
倍角,三倍角,半角の公式
倍角,三倍角,半角の公式
加法定理から導出できる三角関数のいろいろな公式です。毎回導出してもよいですし,時短のために覚えてもよい公式です。
倍角の公式:
三倍角の公式:
半角の公式:
詳しい説明:
三倍角の公式:基礎からおもしろい発展形まで
2倍角の公式とその証明
三角関数の合成公式
三角関数の合成公式
と が混ざった式を, だけで表す公式です。覚えておくべき公式です。
( と のいずれかが でないとき)
ただし, は , を満たす角度。
詳しい説明: 三角関数の合成のやり方・証明・応用
三角関数の和積,積和公式
三角関数の和積,積和公式
三角関数の「和」を「積」に直したり,「積」を「和」に直す公式です。公式を丸ごと覚えるのではなく,導出の流れを覚えておくのがおすすめです。
和積公式:
積和公式:
詳しい説明: 積和公式の導出と覚え方,和積公式の覚え方と証明:覚えるべきか毎回導出すべきか?,
発展: 和積,積和公式の三変数バージョンも存在します。数学オリンピックなどの難しい図形の問題でしばしば応用される公式です。 →三角形の内角における和積公式
三角関数の加法定理に関係する公式たちは,基本の3つから全て高速で導出できるようになってくのが望ましいです。