東大文系数学2017入試過去問解答解説
※以下の解答と解説は東京大学が公表したものではなく,当サイトオリジナルのものです。問題は東京大学第2次試験問題からの引用です。
この記事では,東京大学の2017年度入学試験の文系数学について解説します。
第一問 [面積の最大値]
第一問 [面積の最大値]
座標平面において2つの放物線 と を考える。ただし は実数で, を満たすものとする。放物線 と 軸および 軸で囲まれる領域の面積を とし,放物線 の の部分と 軸および 軸で囲まれる領域の面積を とする。 と がただ1点を共有するとき, の最大値を求めよ。
-
図形量(面積・体積など)の最大・最小を求める問題では,文字を使って図形量を表し,それを関数とみるのが鉄則です。その際「その関数はいくつの変数で表せるのか」が大事です。1変数関数ならば微分により最大・最小はすぐに求まりますが,多変数関数では文字固定など工夫が必要です。
-
図形量を表すのに必要な変数の個数は,基本的にはその図形の自由度に等しいです。自由度とはその図形を決定するのに必要な条件の数です。例えば三角形の場合は3辺,2辺挟角など,3つの条件が決まれば一意に定まるので,自由度は3です。→三角形の決定条件と自由度
-
本問では の2文字で表せるので,自由度は高々2です。ここで, をある値に定めると のグラフが決まり,さらに は「 とただ1点を共有する」という条件から一意に定まります。つまり,ひとつの条件で図形全体が定まるので,自由度は1です。
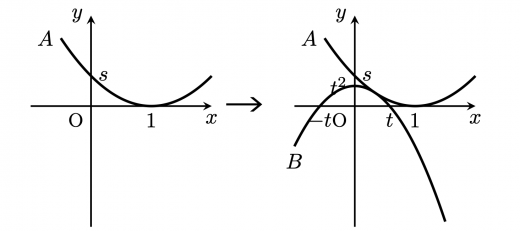
ここから, は文字消去をして1変数関数として表せそうです。文字消去に必要な の関係式は が接する条件から求められそうですね。
このように,大雑把に解答の道筋を考えてから解き始められるといいでしょう。
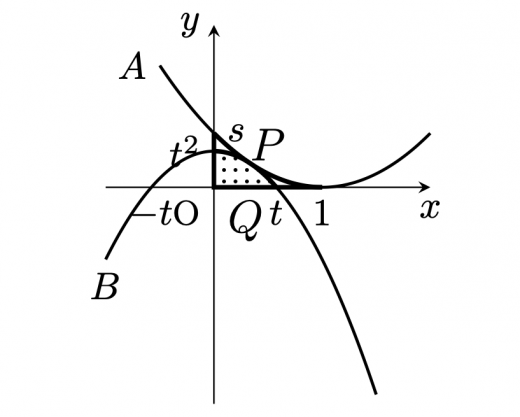
は で 軸と接するので, は,
また, と 軸の交点の 座標は なので, は
以上 と, より,
と分かる。
次に, はただ1点を共有するので, は接する。 ここで, を連立して を消去すると,
となる。 より二次方程式であり,接するという条件から判別式を とおくと が成り立つ。 ここで,
より,
このとき, を満たす全ての で, となるので, が成立する。
<!-- 文字消去したら変域を確認! -->
これと より,
これを とおくと,
よって, における の増減は以下のとおり→増減表の書き方と例題
よって の最大値は
式は の1次式で の2次式です。また, は の3乗と の1乗の形が入っています。文字を消去する際には, ではなく を消去するのがよいでしょう。
文字消去した後は, の3次式になるので,微分すれば最大値が求まります。
第二問 [ベクトルの終点範囲]
第二問 [ベクトルの終点範囲]
1辺の長さが の正六角形 が与えられている。 点 が辺 上を,点 が辺 上をそれぞれ独立に動くとき,線分 を に内分する点 が通りうる範囲の面積を求めよ。
軌跡,領域の問題では座標やベクトルを使って解くことが多いです。線分上や内分点といった条件からベクトルの方が使いやすそうです。また,正六角形で が多く出てきそうなところからも座標を敬遠したくなります。
本問では がそれぞれ独立に動き,それぞれの動きで の位置が変わるので,自由度は2です。 を2つのパラメータで表しましょう。
がそれぞれ線分 上にあるので, を を満たす実数として,
とおける。
は を に内分するので,
ここで, とおくと, は定ベクトルなので, の動く範囲は の終点の動く範囲と等しい。
を の範囲である値に固定したときの, での の範囲を考える。
この範囲は, の終点を通り と平行な直線のうち, 進んだところまでの線分で,以下のようになる。
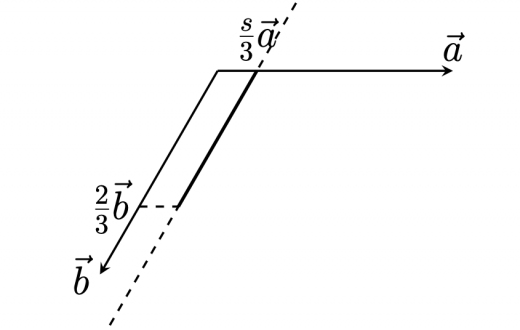
次に, の固定を解除すると より,上図の線分が 向きの成分が から までの範囲にくるように平行移動するので, の取りうる範囲は以下。

ここで, と のなす角は と のなす角に等しく であり,また大きさはそれぞれ なので,
求める面積は
今回は終点範囲を求める部分の比重が高いので答案の中でも文字固定をして丁寧に書きました。問題の中での終点範囲を求める部分の比重が低い場合,もう少し簡潔に書いてもかまわないでしょう。
ベクトルを使わず,図形の範囲を考える別解もあります。ここでは略解を載せておきます(答案が書きにくくおすすめしません)。
まず を固定して とおき, を 上で動かすと, は と平行な線分 上を動く。
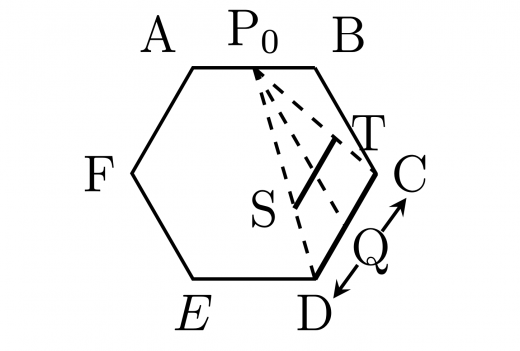
次に を動かすが,そのときの の取りうる範囲は線分 の通過する領域といえる。
ここで, は が に, は が にあるときの なので,それぞれの軌跡は下の左図 のようになる。
よって,線分 は, から までを平行移動すると分かり, の取りうる範囲は下の右図の太線の平行四辺形と分かる。

よって面積は (以下略 : 辺の長さと角度を求めて計算しましょう。
を動かしたとき の軌跡が線分になる(歪んでいない)ことに言及しないと平行四辺形とはいえません。
入試の時間内に完璧な答案を書くのは難しいでしょう。
第三問 [確率]
第三問 [確率]
座標平面上で 座標と 座標がいずれも整数である点を格子点という。格子点上を次の規則 に従って動く点 を考える
最初に,点 は原点 にある。
ある時刻で点 が格子点 にあるとき,その 秒後の点 の位置は,隣接する格子点 ,,, のいずれかであり,また,これらの点に移動する確率は,それぞれ である。
最初から 秒後の点 の座標を とする。 となる確率を求めよ。
点 が,最初から 秒後に直線 上にある確率を求めよ。
理系第二問の の誘導を丁寧にした問題です。
は 秒後の点 の座標を考えれば簡単に解けますね。
点 が原点から 秒後に到達しうる座標は,
の4つであり,順に は となる。
それぞれの点に移る確率は ずつなので,求める確率は
では「直線上」の条件に戸惑う人も多いでしょう。
そこで, の存在意義を考えましょう。小問が複数ある問題では,前の小問の答えの値を利用して解いたり,前の小問での考え方がヒントになったりすることが多いです。
と「直線」の条件の関係を考えたときに, と変換できると, で求めたのは 上にある確率であることに気付けます。

ここまで来れば, あるいは問題文より, 秒ごとに傾き の直線の 切片がそえぞれ の確率で 変化することもわかりますね。
秒後の点 は 上にあるが, 秒後に に移動すると, 上に, に移動すると, 上に移動する。
つまり, 秒たつと ずつの確率で,点 を通り傾きが の直線の 切片が 増減することがわかる。
ここで,最初に点 は 上にあって, 切片は である。 秒後に点 を通る傾き の直線の 切片が であるのは, 切片は に 回, に 回移動する場合である。
よって,求める確率は
上の解説では,簡単に 切片の増減に着目できるかのように書いていますが,すぐには思いつかないかもしれません。その場合は 秒後の点の位置を考えてみたり図を書いてみたりすると,法則をつかみやすいです。
第四問 [数列,整数]
第四問 [数列,整数]
とおき,自然数 に対して
と定める。以下の問いに答えよ。ただし設問 は結論のみを書けばよい。
の値を求めよ。
とする。積 を, を用いて表せ。
は自然数であることを示せ。
と の最大公約数を求めよ。
理系の第四問と同じでした。誘導も丁寧で解きやすい問題です。
は計算するだけです。詳しくは,→分母の有理化や実数化について,→分母の有理化の方法と例題6問
も を計算してみるとわかります。
<!-- 分数の有利化 -->
のとき
を解くときに で求めた を代入したくなるかもしれませんが,その場合 となってしまい, で表せません。
は直接示すのは難しそうです。全ての自然数に関する命題で,直接示すのが難しそうな場合は,帰納法が機能する場合が多いです。→数学的帰納法をわかりやすく【例題3問、応用5パターン】
帰納法を使うために必要なことはなんでしょうか。後ろの項(例えば )を前の項(例えば )を使って表すことですね。ここまで考えて, と繋げられると完璧です。
今回は を使って, を表せますね。
より, で
が成立する。
ここで, は自然数であることを数学的帰納法で示す。
のとき
より,自然数である。
で が自然数になると仮定する。
このとき, なので より,
が成立し,仮定より が自然数なので, が自然数になる。
つまり, で題意を満たすとき, でも題意をみたす。
以上 より,数学的帰納法で示された。
公約数に関する式変形で有名なものといえばユークリッドの互除法でしょう。→ユークリッドの互除法の証明と不定方程式
の式をよく見ると,互除法を有効に使えそうな形をしています。
自然数 の最大公約数を と表すことにする。
このとき, の範囲で を で割った商とあまりについて考えると,
- より が成立する
- 漸化式より
となるので,商は であまりは である。よって,ユークリッドの互除法より
となる。
よって, の範囲で は一定となる:
より, なので,求める最大公約数は
互除法なんて思いつかない!!という場合は, あたりの値を の式を使って計算してみるとよいでしょう。
となりますので,ここからどの隣り合う2数も最大公約数が と気付けると,互除法に近づけるのではないでしょうか。
東大文系数学2017入試過去問解説まとめ
東大文系数学2017入試過去問解説まとめ
例年通りの難易度でした。
第一問は問題文が長く,わかりにくかったでしょう。しかし,図を書いて整理すれば解けなくはない難易度です。
第三問,第四問の後ろの小問は解き方が思いつかないものもあったでしょうが,誘導の意図を組む練習になります。
計算量も少なく,解法がわかれば解き切れる問題量です。
微積,ベクトル,確率,整数とバランスの取れた出題だったと思います。









