東大文系数学2018入試過去問解答解説
※以下の解答と解説は東京大学が公表したものではなく,当サイトオリジナルのものです。問題は東京大学第2次試験問題からの引用です。
この記事では,東京大学の2018年度入学試験の文系数学について解説します。
第一問[図形と方程式]
第一問[図形と方程式]
座標平面上に放物線 を で定め,領域 を で定める。原点を通る2直線 は に接するものとする。
(1) 放物線 上を動く点 と直線 の距離をそれぞれ とする。 が最小値をとるときの点 の座標を求めよ。
(2) 次の条件を満たす点 の動きうる範囲を求め,座標平面上に図示せよ。
条件:領域 のすべての点 に対し不等式 が成り立つ。
問題文が長めでごちゃごちゃしているので,最初は何をすれば良いか少し戸惑うかもしれません。とにかく の方程式を求めなければ何もできないので,まずは の方程式を求めます。
の方程式がわかれば,,そして を求めることができます。
とおく。 を微分して, これより, における接線の方程式は(→微分を用いた接線の方程式の公式) これが を通るとき よって, に接する原点を通る2直線は とわかるので, とおける。
点 の座標を とおく。 との距離 はそれぞれ,(→点と直線の距離の公式の3通りの証明)
よって とおけば, よって, のグラフは以下のようになる。

したがって, のとき,つまり で最小値をとる。
を求めた段階で手が止まってしまった人もいるかもしれません。 絶対値の中が二次関数で,しかもそのルートをとった和を考えなければなりません。そのままでは計算が複雑すぎて解けない未来が見えるでしょう。
しかし,絶対値の中をよく観察すると,どちらも の形で表せそうですね。出題者が単純な ではなく, を考えさせた理由はここにあったのです。
因数分解に気づいてしまえばなんてことはないのですが,ハマってしまうと何もできなくなってしまいます。そんなときは,もう一度問題文をよく観察し,出題者はなぜルートを考えさせたのだろう,とメタ的な視点を持つことで突破できる場合もあります。
ちなみに, は二次関数なので, の方程式は判別式を用いて求めることもできます。
原点を通る直線を とおいて, を連立すると, この方程式の判別式を とすると, よって, に接する原点を通る2直線は とわかる。
以下同様。
次に(2)の問題に移ります。 という式をよく観察してみてください。この式がベクトルの内積のように見えませんか? と考えるということです。
上の点 に対し, であることを利用すると, が満たすべき条件はあらゆる に対して, である。 が原点を含まないことから であるので, は「 または と のなす角が 以上」であることと同値である。
原点を通り に垂直な直線は であるから, の動きうる範囲は であれば良い。 これを図示すると以下の図の斜線部分となる。ただし,境界は領域に含める。
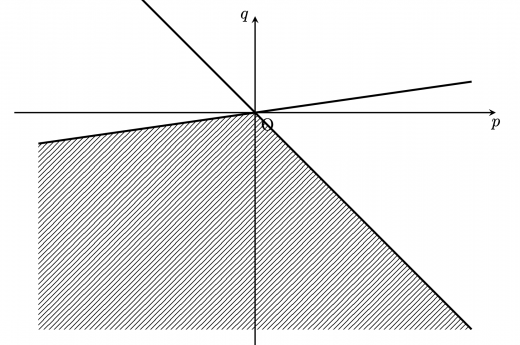
「ベクトルの内積」を思いつけばこのようにスマートに解けます。ですが,こんなに上手い答案を本番の試験でかける人はなかなかいないでしょう。本番で使える正直な方法も紹介します。
満たすべき不等式 が の一次式という簡単な形をしているので, の形にすぐに変形したくなりますが,飛びつかないように注意しましょう。 の値によって場合分けする必要がありますね。
(i) のとき
不等式は となる。領域 内の全ての点 においてこれが成立するのは のときである。
(ii) のとき
不等式は となる。領域 内の全ての点 においてこれが成立するような場合は存在しない。
(iii) のとき
不等式は となる。領域 内の全ての点 においてこれが成立するのは以下のような図を考えると,

よって かつ となれば良い。
以上(i),(ii),(iii)を統合して, の動き得る範囲は
第二問[整数]
第二問[整数]
数列 を, で定める。
(1) と の大小を調べよ。
(2) とする。 を満たす の範囲を求めよ。
(3) が整数となる をすべて求めよ。
(1)に関してはただの計算問題です。約分ミスをしないように気をつけましょう。
(2)も比較的単純な計算問題です。コンビネーションをどのように数式で表すか忘れてしまった人はよく確認しておいてください。→順列と組合せの違いと例題
一般に, であることを思い出すと, これより, という条件を変形していくと, よって, または となるが, より, であり, は整数であるから
本題の(3)です。(1),(2)は簡単な計算問題ですから,最後の(3)で何かしら利用させるための誘導と予想できます。そう考えて問題をよく観察してください。
(2)における とは何を意味するでしょうか。 は定義から正の値ですから,分母を払ってよく,この式は と同値です。この不等式は で成立しますから,書き下すと ということです。
さらに(1)より, ですので,これと合わせると より小さければ整数になんてなるわけないですね。ということは の範囲を頑張って調べれば良いことになります。
このように,前半が簡単な問題のときは後半でその結果を利用することがよくあります。
(2)により, のとき であるから (1)から に注意すると, となり, なので が整数となるのは に限られる。 よって, が答えとなる。
第三問[微分]
第三問[微分]
とし, とおく。
(1) で が単調に増加するための, についての条件を求めよ。
(2) 次の2条件を満たす点 の動きうる範囲を求め,座標平面上に図示せよ。
条件1:方程式 は相異なる3実数解をもつ。
条件2:さらに,方程式 の解を とすると である。
理系と共通の問題です。
が単調に増加することを示す一番簡単な方法は, が非負であることを示すことでしょう。
この問題における導関数は簡単に因数分解できますし,さらに であるため面倒な場合分けも必要ありません。
を微分して よって, の増減表は以下のようになる。 これより, の範囲で が単調増加する条件は, であり, と合わせて
(2)について,条件1を考えるのは簡単です。グラフを見ればすぐにわかります。
条件2をどのように数式に落とし込むかがポイントです。状況を整理するためにまず図を必ず描きましょう。 が3つの解を持っているので,真ん中の解 は より小さいことがわかります。よって必要条件として が必ず満たされていなければなりません。
この下で, は と の間に入っていればよく,それを実現するには の直線が と の間にある位置関係となれば良いということがわかります。
条件1により, のグラフから考えると,相異なる3実数解を持つためには が必要である。
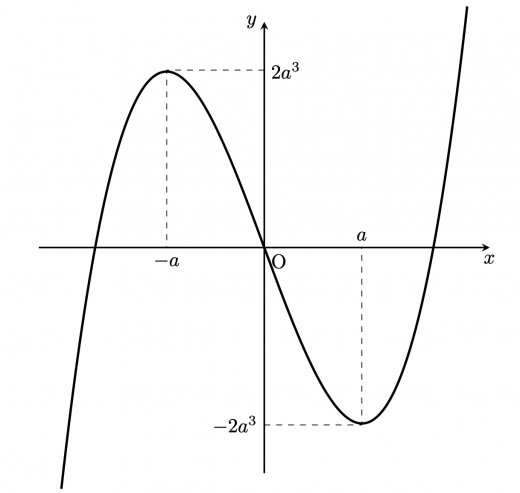
この下で, を満たす が を満たすためには, が必要である。
このとき,条件2は で表すことができる。
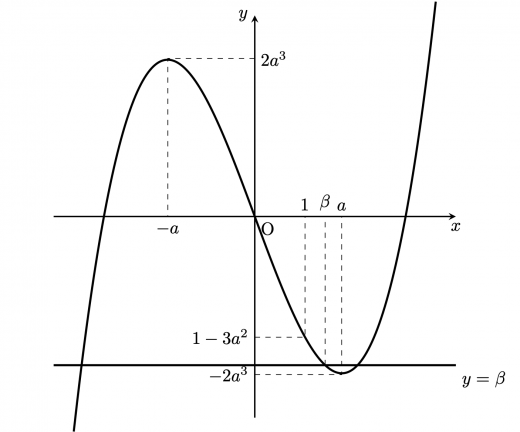
つまり,まとめると,
かつ かつ
が求める範囲である。さらに, のとき, に注意すると,上記の範囲は,
かつ
と単純化できる。これが答えであり,図示すると以下のようになる。
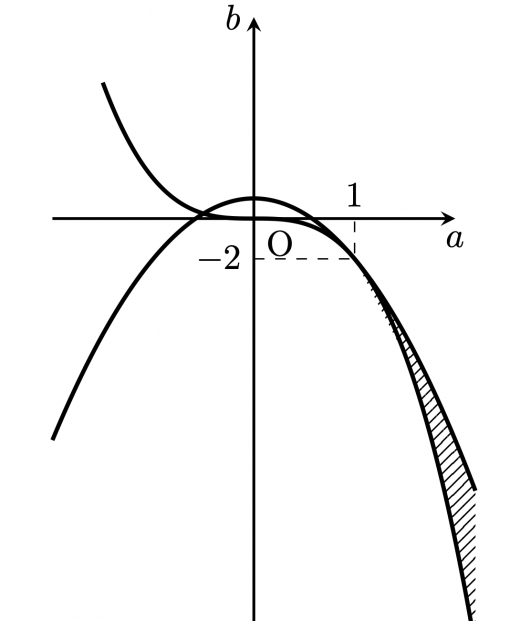
ただし, と において,これらを連立すると よって, でこれらは交わり,特に においては接することに注意。
がもし より小さかったらどうなるか・・・などと考えて手が止まってしまった人もいるかもしれませんが, は必要条件です。すぐに答えにたどり着こうとせずに,「何が満たされていなければならないか」という必要条件を最初にいくつか考え,考えるべき状況を絞っておくと,問題が解きやすくなることがあります。
第四問[ベクトル・軌跡・積分]
第四問[ベクトル・軌跡・積分]
放物線 のうち を満たす部分を とする。座標平面上の原点 と点 を考える。
(1) 点 が 上を動く時, を満たす点 の軌跡を求めよ。
(2) 点 が 上を動き,点 が線分 上を動くとき, を満たす点 が動く領域を座標平面上に図示し,その面積を求めよ。
(1)はとても簡単な軌跡の問題です。 とおいて,問題の条件を同値変形していくことを考えます。
とおくと, が満たすべき条件は
である。 とおくと, は以下の式と同値である。
以上3式を満たす が存在するような の条件を求めればよく, を に代入して,
よって,
が求める軌跡であり,図示すると下図のようになる。
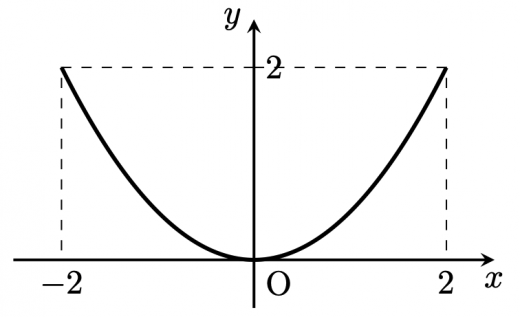
(2)については,(1)の結果を利用するのがよいでしょう。 は を だけ平行移動させた点だと考えると, の軌跡である放物線を,右に だけ移動させたときの通過領域を考えれば良いことがわかります。イメージとしては次のようなものを想像しましょう。

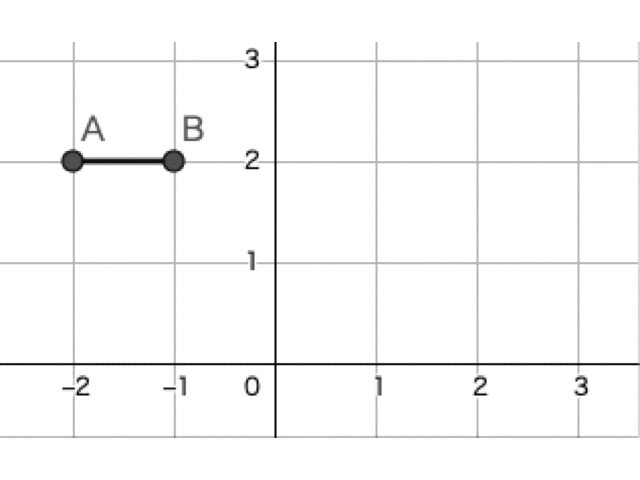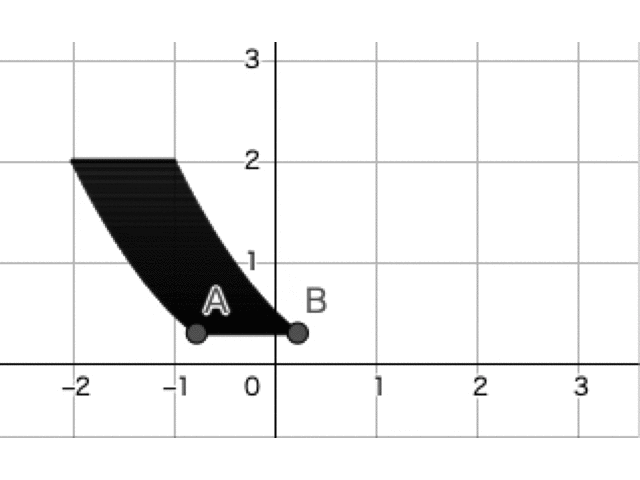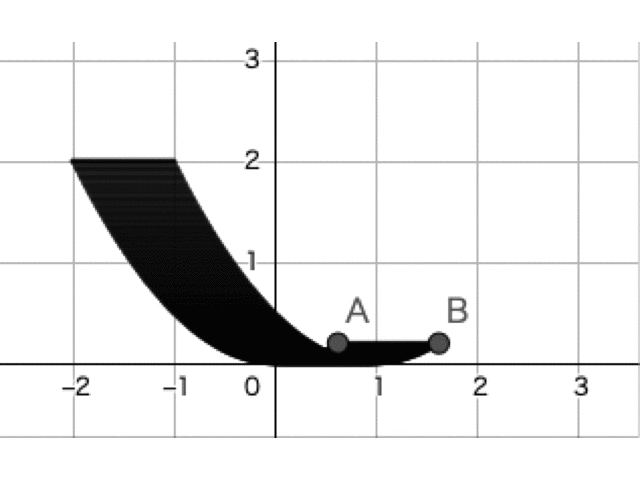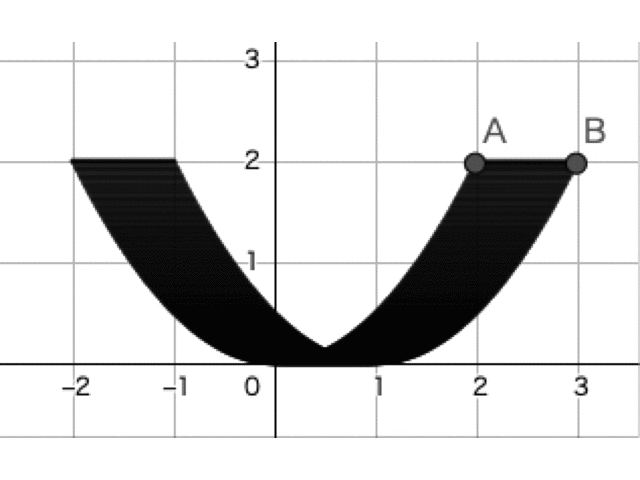
は右向きで,長さが から まで動くベクトルである。つまり,(1)で求めた軌跡を右に 移動させた際の通過領域が の動く範囲である。図示すると以下の斜線部である。ただし,境界は領域に含まれる。

を軸として図形は対称であるから,求めたい面積を とすると,
(1)の誘導を利用しない別解も紹介します。 以下のように,文字を固定して考える方法はよく使われますので,勉強しておきましょう。
とおくと, が満たすべき条件は である。 とおくと, は以下の式と同値である。 以上4式を満たす が存在するような の条件を求めればよい。
さて, で を固定する。 で を動かすと は以下の範囲を動く: よって,以下を満たす が存在するような を求めればよい: で を動かせば先の解答と同じ図を得る。 以下同様。
を動かすのが少々大変かもしれませんが,以下のような線分 の動きのイメージをもてるようになりましょう。
東大文系数学2018入試過去問解説まとめ
東大文系数学2018入試過去問解説まとめ
変にひねった問題はなく,問題を読んですぐに大雑把な方針は立てられるような出題が多かったです。しかし,計算量はそれなりに多く100分で全てを解き切るのはなかなか難しいでしょう。
また,この年度の出題の特徴として,誘導が(過剰なほど)丁寧だったことがあげられます。簡単な問題の後には,その問題の過程や結果を使う問題が続くと身構えておきましょう。
また,図形と方程式の分野からの出題が目立ちました。特に軌跡の問題は東大が好んで出しますので,よく復習しておきましょう。また,図を丁寧にかつ素早くかけるようになると,点数アップにつながるかもしれません。
個人的には確率の分野からの出題がなくて少し残念です。









