東大理系数学2018入試過去問解答解説 | 高校数学の美しい物語

第一問[微分・極限]

第一問

$f(x) = \dfrac{x}{\sin x} + \cos x ~~ (0 < x < \pi)$ の増減表をつくり， $x \rightarrow +0,~x \rightarrow \pi - 0$ のときの極限を調べよ。

六問の中では一番解きやすいです。東大入試の第一問は易しい問題が出る傾向がありますね。

増減表を調べよと言われていますから，とにかくまずは微分します。導関数を整理していくと， $\sin 2x - 2x$ の正負を評価することになりまます。ここで，三角関数における非常に有名な不等式 $\sin x \leq x ~~ (0 \leq x)$ 特に $0 < x$ では $\sin x < x$ が成立することを思い出したいところです。（ジョルダンの不等式とその３通りの証明やマクローリン型不等式（三角関数）で紹介しています。）

また，極限を求めるのもあまり難しくありません。三角関数の極限の問題では変数 $\to 0$ になるように置換するとうまくいくことが多いです。

第一問

$f(x)$ を微分して， $\begin{aligned} f'(x) &= \dfrac{\sin x - x \cos x}{\sin ^2 x}- \sin x\\ &= \dfrac{\sin x \left(1-\sin^2 x\right)-x\cos x}{\sin^2 x}\\ &= \dfrac{\cos x \left(\sin x \cos x - x\right)}{\sin^2 x}\\ &= \dfrac{\cos x \left(\sin 2x -2x\right)}{2\sin^2 x} \end{aligned}$ ここで $0 < x$ では $\sin x < x$ が成立するので， $\sin 2x - 2x$ は $0 < x < \pi$ の範囲で負である。よって $f(x)$ の増減表は以下の通り。

$\begin{array}{c|ccccc} x & 0 & \cdots & \dfrac{\pi}{2} & \cdots & \pi \\ \hline f’(x) & & - & 0 & + & \\ \hline f(x) & \displaystyle\lim_{x\to +0}f(x) & \searrow & \dfrac{\pi}{2} & \nearrow & \displaystyle\lim_{x\to \pi -0}f(x) \end{array}$

また，極限について， $\lim_{x\to +0}f(x) = 1+1 = 2$ さらに， $y = \pi - x$ とおくと $\begin{aligned} f(x) &= \dfrac{\pi - y}{\sin (\pi - y)} + \cos(\pi - y)\\ &= \dfrac{\pi - y}{\sin y} - \cos y \end{aligned}$ より $\begin{aligned} \lim_{x\to \pi -0}f(x) &= \lim_{y \to +0}\left\{\dfrac{\pi - y}{\sin y} - \cos y\right\} \\ &= + \infty \end{aligned}$

ちなみに，さらに二階微分などを計算すると，グラフの概形は以下のようになります。練習問題として書いてみてはどうでしょうか。

第一問概形

$\sin 2x - 2x$ の正負を評価する際，上記の不等式を知らない場合どうすれば良いでしょうか。応用が効くアドバイスとして，「微分しても正負が評価できない時は，もう一度微分してみる」とよいでしょう。別解として以下に記します。

第一問別解

$f(x)$ を微分するところまでは同じ。

$g(x) = \sin 2x - 2x$ とおいて， $g(x)$ を微分すると， $\begin{aligned} g'(x) &= 2 \cos 2x - 2\\ &= 2(\cos 2x - 1)\\ &\leq 0 \end{aligned}$ よって $g(x)$ は単調減少であり， $g(0) = 0-0 = 0$ であることと合わせると $0 < x < \pi$ では $g(x) < 0$ である。

以下同様。

微分しても符号がわからなくて困ってしまったときは，このことを思い出してください。

ちなみに $\dfrac{\sin x}{x}$ という形はsinc関数と呼ばれる有名な関数です。工学的に意味のある関数としても知られていて，よく大学入試の題材として取りあげられます。→sinx/xについて覚えておくべき２つのこと

第二問[整数]

第二問

数列 $a_1, a_2, \cdots$ を， $a_n = \dfrac{{}_{2n+1}\mathrm{C}_n}{n!}$ $(n = 1,2,\cdots)$ で定める。

(1) $n \geq 2$ とする。 $\dfrac{a_n}{a_{n-1}}$ を既約分数 $\dfrac{q_n}{p_n}$ として表したときの分母 $p_n \geq 1$ と分子 $q_n$ を求めよ。

(2) $a_n$ が整数となる $n \geq 1$ をすべて求めよ。

(1)について，既約分数として表した時を考えるので，分母と分子が互いに素の関係になるようにする必要があります。互いに素かどうか，つまり最大公約数が $1$ かどうかを考えるには，ユークリッドの互除法が便利です。→ユークリッドの互除法の証明と不定方程式

第二問(1)

${}_m \mathrm{C}_n = \dfrac{m!}{n!(m-n)!}$ より（コンビネーションの定義を忘れてしまった人は→順列と組合せの違いと例題） $\begin{aligned} \dfrac{a_n}{a_{n-1}} &= \dfrac{{}_{2n+1}\mathrm{C}_n}{n!} \times \dfrac{(n-1)!}{{}_{2n-1}\mathrm{C}_{n-1}}\\ &= \dfrac{1}{n} \times \dfrac{(2n+1)!}{n!(n+1)!}\times \dfrac{(n-1)!n!}{(2n-1)!}\\ &= \dfrac{2(2n+1)}{n(n+1)} \end{aligned}$ ここで， $n(n+1)$ は連続する2つの整数の積であるから， $2$ の倍数である。（→連続するn個の整数の積と二項係数）よって，この分数は $2$ で約分ができて， $\dfrac{a_n}{a_{n-1}} = \dfrac{2n+1}{\left\{\frac{n(n+1)}{2}\right\}}$ とかける。これが既約分数であることを証明する。ユークリッドの互除法により， $\begin{aligned} \gcd(2n+1, n) &= \gcd(n,1)\\ \gcd(2n+1, n+1) &= \gcd(n,n+1) = \gcd(n,1) \end{aligned}$ である， $\gcd(n,1) = 1$ は明らかなので， $2n+1$ と $n(n+1)$ は互いに素である。つまり，さきほどの分数が既約分数であることが証明できた。

よって $p_n = \dfrac{n(n+1)}{2}, ~~~q_n = 2n+1$

次に(2)です。(1)の $\dfrac{a_n}{a_{n-1}}$ をどのように解釈するかがポイントです。2通りの解釈の方法を紹介します。

1つは「漸化式」としてみることです（東大はこちら側の解答を想定していると思われます）。 $n\geq 2$ に対して，漸化式を繰り返し用いると， $\begin{aligned} a_n &= \dfrac{q_n}{p_n} a_{n-1} \\ &= \dfrac{q_n}{p_n} \dfrac{q_{n-1}}{p_{n-1}} a_{n-2}\\ &= \dfrac{q_n}{p_n} \dfrac{q_{n-1}}{p_{n-1}}\dfrac{q_{n-2}}{p_{n-2}} a_{n-3}\\ &= \cdots\\ &= \dfrac{q_n}{p_n} \dfrac{q_{n-1}}{p_{n-1}}\cdots \dfrac{q_2}{p_2} a_{1} \end{aligned}$ となります。(1)では既約分数を考えましたから，約数についてなにか解決の糸口がないかを考えます。すると $q_n$ は常に奇数であり $2$ を約数として持たないことに注目できます。よって， $n$ が大きくなって分母に素因数 $2$ が余分に出てきてしまえば，整数にはならなくなります。

この議論を用いて解答を作ります。

第二問(2)

$a_1 = \dfrac{{}_3 \mathrm{C}_1}{1!} = 3, ~ a_2 = \dfrac{{}_5 \mathrm{C}_2}{2!} = 5$ より， $n = 1,2$ のとき題意をみたす。さて， $n \geq 2$ に対し $a_n = \dfrac{q_n}{p_n} \dfrac{q_{n-1}}{p_{n-1}}\cdots \dfrac{q_2}{p_2} a_{1}$ が成立する。この式において， $q_n, q_{n-1}, \cdots, q_2$ は全て奇数であり， $a_1$ も奇数であるから，分子に $2$ を約数として含まない。これに対し， $p_3 = 6$ であって $2$ を約数に含むので， $p_3$ が分母にある $a_n$ は整数になり得ない。つまり， $n \geq 3$ は答えに含まれない。よって答えは $n = 1,2$

2つ目は， $\dfrac{a_n}{a_{n-1}}$ を「比」としてみることです。(1)の計算結果からわかるように，分母は二次式，分子は一次式です。 $n$ が大きくなれば0に近づいていくはずです。よって $a_n$ は減少し，あるときから $1$ より小さくなって整数になり得なくなるでしょう。したがって，有限個の $a_n$ を確認すれば全ての答えを導けそうです。

第二問(2)

まず， $\dfrac{a_n}{a_{n-1}} < 1$ が成立する範囲を考える。 $\begin{aligned} \dfrac{2(2n+1)}{n(n+1)} &< 1\\ 4n + 2 &< n^2 + n\\ n^2 -3n -2& > 0\\ n &> \dfrac{3 + \sqrt{17}}{2}\\ n &\geq 4 \end{aligned}$ これより， $a_3 > a_4 > a_5 > \cdots$ である。さて， $a_1 = 3, ~ a_2 = 5, ~ a_3 = \dfrac{35}{6},\\ ~ a_4 = \dfrac{21}{4}, ~ a_5 = \dfrac{77}{20},\\ ~ a_6 = \dfrac{143}{60}, ~ a_7 = \dfrac{143}{112}, ~ a_8 = \dfrac{2431}{4032}$ であり， $a_8 < 1$ より $1 > a_8 > a_9 > a_{10} > \cdots$ であるから， $n \geq 8$ においては $a_n$ は整数になり得ない。よって $n = 1,2$

第三問[ベクトル・軌跡・積分・極限]

第三問

放物線 $y = x^2$ のうち $-1\leq x \leq 1$ を満たす部分を $C$ とする。座標平面上の原点 $O$ と点 $A(1,0)$ を考える。 $k > 0$ を実数とする。点 $P$ が $C$ 上を動き，点 $Q$ が線分 $OA$ 上を動くとき， $\overrightarrow{OR} = \dfrac{1}{k} \overrightarrow{OP} + k\overrightarrow{OQ}$ を満たす点 $R$ が動く領域の面積を $S(k)$ とする。 $S(k)$ および $\displaystyle\lim_{k\to +0}S(k), \lim_{k\to \infty}S(k)$ を求めよ。

なかなか骨のある軌跡の問題です。軌跡の問題は大まかに2つの考え方があります。**「軌跡を想像して解く方法」と「数式をいじって解く方法」**です。まずは前者を考えます。

まず問題設定より， $P,Q$ は独立して動きます。 $Q$ の方が単純な動きをしますから，後から考えた方がよさそうです。 $Q$ を固定して考えます。 $P$ は $C$ 上を動きますから， $\dfrac{1}{k}\overrightarrow{OP}$ により表される点は放物線上を動きます。その後 $Q$ を動かします。 $R$ が $\dfrac{1}{k}\overrightarrow{OP}$ を $k\overrightarrow{OQ}$ だけ平行移動させた点だと考えると，放物線を右に $k$ だけ移動させたときの通過領域を考えれば良いことがわかります。

注意として，放物線を右に移動させるときに， $k$ の値によって領域の形が変わることに気をつけてください。次の2通りの領域のでき方がありますね。

klarger2

ksmaller2

第三問

$P(a,b),~Q(t,0)$ とおくと， $(a,b),(t,0)$ が満たすべき条件は $\begin{cases} b = a^2\\ -1 \leq a \leq 1\\ 0 \leq t \leq 1 \end{cases}$ である。 $R(x,y)$ とおくと， $\overrightarrow{OR} = \dfrac{1}{k} \overrightarrow{OP} + k\overrightarrow{OQ}$ は以下の式と同値である。 $\begin{pmatrix} x\\ y\\ \end{pmatrix} = \dfrac{1}{k} \begin{pmatrix} a\\ b\\ \end{pmatrix} + k \begin{pmatrix} t\\ 0\\ \end{pmatrix}$ $b = a^2$ を代入し，その後に $a = k(x-kt)$ を代入して整理すると $\begin{cases} -\dfrac{1}{k} + kt \leq x \leq \dfrac{1}{k} + kt\\ 0 \leq t \leq 1\\ y = k(x-kt)^2 \end{cases}$ となる。これら3式を満たす $t$ が存在するような $(x,y)$ の条件を求めれば良い。

ここで $t$ を $0 \leq t \leq 1$ で動かすと， $R$ が動く領域は以下の斜線部のようになる。

(i) $\dfrac{1}{k} \leq k-\dfrac{1}{k}$ のとき，つまり $k \geq \sqrt{2}$ のとき

第三問(i)

図より， $\begin{aligned} S(k) &= k \times \dfrac{1}{k} + 2\int_0^{\frac{1}{k}} \left(\dfrac{1}{k} - kx^2\right)dx\\ &= 1 + 2\left[\dfrac{1}{k}x - \dfrac{k}{3} x^3\right]_0^{\frac{1}{k}}\\ &= 1 + 2\left(\dfrac{1}{k^2} - \dfrac{1}{3k^2}\right)\\ &= 1 + \dfrac{4}{3k^2} \end{aligned}$

(i) $\dfrac{1}{k} > k-\dfrac{1}{k}$ のとき，つまり $(0 < )~k < \sqrt{2}$ のとき

第三問(ii)

図より， $\begin{aligned} \dfrac{S(k)}{2} &= \int_{\frac{k}{2}}^{\frac{1}{k}}kx^2 dx\\ &+ \left\{\left(k + \dfrac{1}{k}\right) - \dfrac{1}{k}\right\} \times \dfrac{1}{k} - \int_k^{k+\frac{1}{k}}k(x-k)^2dx\\ &= \left[\dfrac{k}{3}x^3\right]_{\frac{k}{2}}^{\frac{1}{k}} + 1 - \left[\dfrac{k}{3}(x-k)^3\right]_{k}^{k+\frac{1}{k}}\\ &= \dfrac{1}{3k^2} - \dfrac{k^4}{24} + 1 - \dfrac{1}{3k^2} \end{aligned}$ $\therefore ~ S(k) = 2 - \dfrac{k^4}{12}$

これらにより， $\begin{aligned} \lim_{k \to +0} S(k) = 2, ~~ \lim_{k \to \infty} S(k) = 1 \end{aligned}$

面積の計算に関しては，どちらの場合も対称性を用いるとラクになります。極限の計算は何も難しくないですね。

次に「数式をいじって解く方法」を考えます。基本的には上の方法の方が計算量が少なくミスも防ぎやすいと思いますが，本番はどうしても緊張しますし，頭が真っ白になってしまって「軌跡が全く想像できない！」なんてこともあるかもしれません。

そんなときに，落ち着いて代入計算による同値変形を黙々とやることが緊張を和らげることに繋がる可能性もあります。以下の方法も試しておくと良いでしょう。

ただし，問題によっては数式だけをつかって解く方法の計算が煩雑すぎて解けないということもあるので注意しましょう。

第三問別解

$P(a,b),~Q(t,0),~R(x,y)$ として， $\begin{cases} b = a^2\\ -1 \leq a \leq 1\\ 0 \leq t \leq 1\\ \begin{pmatrix} x\\ y\\ \end{pmatrix} = \dfrac{1}{k} \begin{pmatrix} a\\ b\\ \end{pmatrix} + k \begin{pmatrix} t\\ 0\\ \end{pmatrix} \end{cases}$ を満たす $a,b,t$ が存在するような $(x,y)$ の条件を考えれば良い，というところまでは同じ。

$b = a^2, ~ t = \dfrac{x-\dfrac{1}{k}a}{k}$ を代入すれば， $\begin{aligned} &\begin{cases} -1 \leq a \leq 1\\ 0 \leq \dfrac{x-\dfrac{1}{k}a}{k} \leq 1\\ y = \dfrac{1}{k} a^2 \end{cases}\\ &\\ &\iff \begin{cases} -1 \leq a \leq 1\\ 0 \leq x-\dfrac{1}{k}a \leq k\\ a = + \sqrt{ky}\\ ky \geq 0 \end{cases} ~\text{または}~ \begin{cases} -1 \leq a \leq 1\\ 0 \leq x-\dfrac{1}{k}a \leq k\\ a = - \sqrt{ky}\\ ky \geq 0 \end{cases} \end{aligned}$ を満たす $a$ が存在するような $(x,y)$ の条件を求めればよい。 $a$ を各式に代入して同値変形すると以下の通り。 $\begin{aligned} &\begin{cases} -1 \leq \sqrt{ky} \leq 1\\ \sqrt{\dfrac{y}{k}} \leq x \leq k+\sqrt{\dfrac{y}{k}}\\ ky \geq 0 \end{cases} ~\text{または}~ \begin{cases} -1 \leq -\sqrt{ky} \leq 1\\ -\sqrt{\dfrac{y}{k}} \leq x \leq k-\sqrt{\dfrac{y}{k}}\\ ky \geq 0 \end{cases}\\ &\\ &\iff\begin{cases} 0 \leq ky \leq 1\\ \sqrt{\dfrac{y}{k}} \leq x \leq k+\sqrt{\dfrac{y}{k}}\\ \end{cases} ~\text{または}~ \begin{cases} 0 \leq ky \leq 1\\ -\sqrt{\dfrac{y}{k}} \leq x \leq k-\sqrt{\dfrac{y}{k}}\\ \end{cases}\\ &\\ &\iff\begin{cases} 0 \leq ky \leq 1\\ -\sqrt{\dfrac{y}{k}} \leq x \leq k-\sqrt{\dfrac{y}{k}} ~~\text{または}~ \sqrt{\dfrac{y}{k}} \leq x \leq k+\sqrt{\dfrac{y}{k}}\\ \end{cases} \end{aligned}$ ここで， $0 \leq ky \leq 1$ のもと， $k-\sqrt{\dfrac{y}{k}} < \sqrt{\dfrac{y}{k}}\\ \iff k^3 < 4y$ であることを考えると， $\begin{aligned} &\begin{cases} 0 \leq ky \leq 1\\ k^3 < 4y\\ -\sqrt{\dfrac{y}{k}} \leq x \leq k-\sqrt{\dfrac{y}{k}} ~\text{または}~ \sqrt{\dfrac{y}{k}} \leq x \leq k+\sqrt{\dfrac{y}{k}} \end{cases}\\ &~\text{または}~ \begin{cases} 0 \leq ky \leq 1\\ k^3 \geq 4y\\ -\sqrt{\dfrac{y}{k}} \leq x \leq k+\sqrt{\dfrac{y}{k}}\\ \end{cases}\\ &\\ \iff&\begin{cases} 0 \leq y \leq \dfrac{1}{k} & (1)\\ \dfrac{k^3}{4} < y & (2)\\ -\sqrt{\dfrac{y}{k}} \leq x \leq k-\sqrt{\dfrac{y}{k}} ~\text{または}~ \sqrt{\dfrac{y}{k}} \leq x \leq k+\sqrt{\dfrac{y}{k}} & (3) \end{cases}\\ &~\text{または}~ \begin{cases} 0 \leq y \leq \dfrac{1}{k} & (4)\\ \dfrac{k^3}{4} \geq y & (5)\\ -\sqrt{\dfrac{y}{k}} \leq x \leq k+\sqrt{\dfrac{y}{k}} & (6)\\ \end{cases}\\ \end{aligned}$ ここで， $\begin{aligned} &\dfrac{k^3}{4} < \dfrac{1}{k}\\ &\iff k^4 < 4\\ &\iff k^2 < 2\\ &\iff 0 < k < \sqrt{2} \end{aligned}$ のとき， $(1)$ かつ $(2)$ は $\dfrac{k^3}{4} < y \leq \dfrac{1}{k}$ また， $(4)$ かつ $(5)$ は $0 \leq y \leq \dfrac{k^3}{4}$ また， $\begin{aligned} &\dfrac{k^3}{4} \geq \dfrac{1}{k}\\ &\iff k \geq \sqrt{2} \end{aligned}$ のとき， $(1)$ かつ $(2)$ は共通部分がなく， $(4)$ かつ $(5)$ は $0 \leq y \leq \dfrac{1}{k}$ よって， $R$ の動く領域は $0 < k < \sqrt{2}$ のとき $\begin{cases} \dfrac{k^3}{4} < y \leq \dfrac{1}{k}\\ -\sqrt{\dfrac{y}{k}} \leq x \leq k-\sqrt{\dfrac{y}{k}} ~\text{または}~ \sqrt{\dfrac{y}{k}} \leq x \leq k+\sqrt{\dfrac{y}{k}} & \end{cases}\\ ~\text{または}~ \begin{cases} 0 \leq y \leq \dfrac{k^3}{4}\\ -\sqrt{\dfrac{y}{k}} \leq x \leq k+\sqrt{\dfrac{y}{k}} \\ \end{cases}$ であるから， $\begin{aligned} S(k) = &\int_{\frac{k^3}{4}}^{\frac{1}{k}}\left\{k-\sqrt{\dfrac{y}{k}}-\left(-\sqrt{\dfrac{y}{k}}\right)\right\}dy\\ &+\int_{\frac{k^3}{4}}^{\frac{1}{k}}\left\{k+\sqrt{\dfrac{y}{k}}--\sqrt{\dfrac{y}{k}}\right\}dy\\ &+\int_{0}^{\frac{k^3}{4}}\left\{k+\sqrt{\dfrac{y}{k}}-\left(-\sqrt{\dfrac{y}{k}}\right)\right\}dy\\ = &\int_{\frac{k^3}{4}}^{\frac{1}{k}}2kdy+\int_{0}^{\frac{k^3}{4}}\left\{k+2\sqrt{\dfrac{y}{k}}\right\}dy\\ = &\left[2ky\right]_{\frac{k^3}{4}}^{\frac{1}{k}} + \left[ky + \dfrac{4}{3}\sqrt{\dfrac{y^3}{k}}\right]_{0}^{\frac{k^3}{4}}\\ = &2 - \dfrac{k^4}{12} \end{aligned}$ また， $R$ の動く領域は $k \geq \sqrt{2}$ のとき $\begin{cases} 0 \leq y \leq \dfrac{1}{k}\\ -\sqrt{\dfrac{y}{k}} \leq x \leq k+\sqrt{\dfrac{y}{k}} \\ \end{cases}$ であるから， $\begin{aligned} S(k) &= \int_{0}^{\frac{1}{k}}\left\{k+\sqrt{\dfrac{y}{k}}-\left(-\sqrt{\dfrac{y}{k}}\right)\right\}dy\\ &= \left[ky + \dfrac{4}{3}\sqrt{\dfrac{y^3}{k}}\right]_{0}^{\frac{1}{k}}\\ &= 1 + \dfrac{4}{3k^2}\\ \end{aligned}$

以下同様。

この方法は同値変形さえうまくやれば図を書かなくて良いことに注目してください。（図示せよという指示があったらこの解法は大変でしょう。）

第四問[微分]

第四問

$a > 0$ とし， $f(x) = x^3 -3a^2x$ とおく。次の2条件を満たす点 $(a,b)$ の動きうる範囲を求め，座標平面上に図示せよ。

条件1:方程式 $f(x) = b$ は相異なる3実数解をもつ。

条件2:さらに，方程式 $f(x) = b$ の解を $\alpha < \beta < \gamma$ とすると $\beta > 1$ である。

本問は2018の東大文系数学の第三問の(2)と全く同じ問題です。詳細な解説は以下を参照してください。

東大文系数学2018入試過去問解答解説

三次関数の問題ですが， $a > 0$ という条件のおかげで増減表をとても簡単に書くことができます。文系の受験生でも取っておきたいレベルです。理系の受験生にとっては絶対に落とせない問題と言えるでしょう。

第五問[複素数]

第五問

複素数平面上の原点を中心とする半径 $1$ の円を $C$ とする。点 $P(z)$ は $C$ 上にあり，点 $A(1)$ とは異なるとする。点 $P$ における円 $C$ の接線に関して，点 $A$ と対称な点を $Q(u)$ とする。 $w = \dfrac{1}{1-u}$ とおき， $w$ と共役な複素数を $\overline{w}$ で表す。

(1) $u$ と $\dfrac{\overline{w}}{w}$ を $z$ についての整式として表し，絶対値の商 $\dfrac{\left|w + \overline{w} -1\right|}{|w|}$ を求めよ。

(2) $C$ のうち実部が $\dfrac{1}{2}$ 以下の複素数で表される部分を $C'$ とする。点 $P(z)$ が $C'$ 上を動く時の点 $R(w)$ の軌跡を求めよ。

複素数平面の問題です。まず，(1)ですが， $Q(u)$ が満たすべき条件をどのように表すか悩むと思います。

簡単に数式化ができる条件の表し方を考えましょう。複素数においては，平行であること，長さが等しいことは簡単に表すことができますので，それらを使って条件を表すことを考えます。 $Q$ が $A$ と対称な点であるためには， $PA = PQ,~OP \parallel AQ$ が満たされていれば良いです。これらは簡単に数式で表すことができます。

第五問(1)

点 $Q$ が点 $A$ と $P$ における $C$ の接線に関して対称な点であるためには， $\begin{cases} PA = PQ\\ OP \parallel AQ \end{cases}$ が満たされていればよい。複素数を用いて数式で表せば， $k~(\neq 0)$ を実数として $\begin{cases} |z-1| = |z-u| && (1)\\ kz = u - 1 && (2)\\ \end{cases}$ で表される。 $P(z)$ が $C$ 上にある，つまり $z\overline{z} = |z|^2 = 1$ であることと， $(2)$ 式に注意しながら， $(1)$ 式を $2$ 乗して， $\begin{aligned} |z-1|^2 &= |z-(kz+1)|^2\\ (z-1)(\overline{z}-1) &= (z-kz-1)(\overline{z}-k\overline{z}-1)\\ 0 &= -2k + k^2 + k(z + \overline{z})\\ 0 &= -2 + k + z + \dfrac{1}{z}\\ \therefore k &= 2 - z - \dfrac{1}{z} \\ \end{aligned}$ これを $(2)$ 式に代入して， $\begin{aligned} u - 1 &= \left(2 - z - \dfrac{1}{z}\right)z\\ \therefore u &= 2z - z^2 \end{aligned}$ よって， $\omega=\dfrac{1}{1-2z+z^2}$ より， $\begin{aligned} \dfrac{\overline{w}}{w} &= \dfrac{1}{1-2\overline{z}+\overline{z}^2} \cdot (1-2z+z^2)\\ &=\dfrac{z^2}{z^2-2z|z|^2+|z|^4}\cdot (1-2z+z^2)\\ &= \dfrac{z^2(1-2z+z^2)}{z^2 -2z + 1}\\ &= z^2 \end{aligned}$ 最後に， $\begin{aligned} \dfrac{\left|w + \overline{w} -1\right|}{|w|} &= \left|1 + \dfrac{\overline{w}}{w} - \dfrac{1}{w}\right|\\ &= \left|1 + z^2 - 1 + 2z - z^2\right|\\ &= 2 \end{aligned}$

「直線に関して対称」を数式で表すことさえできれば，あとは単純な計算問題です。

他にも「直線に関して対称」を表す方法は多数あります。以下で一例をあげておきます。

第五問(1)別解

$A$ と $Q$ の中点を $B(b)$ とすると， $OP \parallel AB$ から，実数 $k$ を用いて $b = 1 + kz$ とおくことができる。 $OP \bot PB$ より， $\begin{aligned} \dfrac{z}{b-z} &= \dfrac{z}{1 + (k-1)z}\\ &= \dfrac{1}{\dfrac{1}{z} + (k-1)} \end{aligned}$ は純虚数であるから， $\begin{aligned} \dfrac{1}{\dfrac{1}{z} + (k-1)} + \overline{\dfrac{1}{\dfrac{1}{z} + (k-1)}} &= 0\\ \dfrac{1}{\dfrac{1}{z} + (k-1)}+\dfrac{1}{\dfrac{1}{\overline{z}} + (k-1)} &= 0\\ \dfrac{1}{z} + (k-1)+\dfrac{1}{\overline{z}} + (k-1)&=0\\ \end{aligned}$ $\begin{aligned} \therefore 2k &= 2 - \dfrac{1}{z} - \dfrac{1}{\overline{z}}\\ &= 2 - \dfrac{1}{z} - z \end{aligned}$ ここで， $u = 1 + 2kz$ であることに注意すると， $u = 2z - z^2$ となる。以下同様。

さて，(2)についてですが，(1)がどのように誘導になっているのか考えるのがとても難しいです。求めさせている絶対値の商の式の形が明らかに不自然なので，この式をどうにかうまく利用できないか考えます。 $\begin{aligned} \dfrac{\left|w + \overline{w} -1\right|}{|w|} &= 2\\ \left|\dfrac{w + \overline{w}}{2} -\dfrac{1}{2}\right| &= |w|\\ \left|\mathrm{Re}(w) -\dfrac{1}{2}\right| &= |w|\\ \end{aligned}$ と変形すると， $xy$ 平面で考えれば， $x = \dfrac{1}{2}$ との距離と，原点 $O$ からの距離が等しい点の集合を表ます。つまり放物線です。 →放物線の準線・焦点と一般化

また， $w$ の動き得る範囲が問題になりますが，これも(1)の結果より， $\begin{aligned} w &= \dfrac{1}{1-2z+z^2}\\ &= \dfrac{1}{(z-1)^2} \end{aligned}$ と変形できることから， $z-1$ の偏角を求めることができれば $w$ の偏角についても求めることができそうです。

第五問(2)

(1)の答えを用いて式変形をすると， $\begin{aligned} \dfrac{\left|w + \overline{w} -1\right|}{|w|} &= 2\\ \left|\dfrac{w + \overline{w}}{2} -\dfrac{1}{2}\right| &= |w|\\ \left|\mathrm{Re}(w) -\dfrac{1}{2}\right| &= |w|\\ \end{aligned}$ これは， $w$ が， $xy$ 平面上において， $x = \dfrac{1}{2}$ を準線， $(0,0)$ を焦点とする放物線上に位置することを表す。つまり， $w = x+iy$ と置いた時に， $\begin{aligned} y^2 &= 4\left(-\dfrac{1}{4}\right)\left(x-\dfrac{1}{4}\right)\\ x &= -y^2 + \dfrac{1}{4} \end{aligned}$ を満たす。

さて， $w$ の動き得る範囲について考える。 $z$ は $C'$ を動くので，そこから $1$ を引いた $z-1$ は次の図の太線円弧上のような範囲を動く。 z-1の動く範囲よって， $\dfrac{2\pi}{3} \leq \arg(z-1) \leq \dfrac{4\pi}{3}\\ \dfrac{4\pi}{3} \leq 2\arg(z-1) \leq \dfrac{8\pi}{3}\\ \dfrac{-8\pi}{3} \leq -2\arg(z-1) \leq \dfrac{-4\pi}{3}\\$ ここで $w = \dfrac{1}{(z-1)^2}$ であることを考えると $\dfrac{-8\pi}{3} \leq \arg w \leq \dfrac{-4\pi}{3}\\ \dfrac{-2\pi}{3} \leq \arg w \leq \dfrac{2\pi}{3}\\$ よって，軌跡を図示すると，以下の太線部のようになる。

第五問(2)

式で表せば，以下の通り： $\begin{cases} y^2 = -x + \dfrac{1}{4}\\ x \geq -\dfrac{1}{2} \end{cases}$

前半部分の上手いやり方を本番で思いつくのはなかなか難しいと思います。今回は， $\dfrac{\left|w + \overline{w} -1\right|}{|w|}$ のなかに $w+\overline{w}$ が入っており， $w = x+iy$ と置いても数式がそれほど複雑にならないので，最初からこの方法で考えてもさほど大変ではないでしょう。（この問題の場合は上手いやり方はないかと考えるよりも，最初からこの方法で考えた方がむしろ早いかもしれません。）

第五問(2)別解

(1)の答え $\dfrac{\left|w + \overline{w} -1\right|}{|w|} = 2$ を， $w = x + iy$ とおいて変形すると， $\begin{aligned} \dfrac{|x+iy + x - iy - 1|}{\sqrt{x^2+y^2}}&=2\\ \dfrac{|2x - 1|}{\sqrt{x^2+y^2}}&=2\\ |2x-1|^2 &= 4(x^2+y^2)\\ \therefore y^2 = -x + \dfrac{1}{4} \end{aligned}$ 以下同様。

第六問[空間図形・積分]

第六問

座標空間内の $4$ 点 $O(0,0,0),~A(1,0,0),~B(1,1,0),~C(1,1,1)$ を考える。 $\dfrac{1}{2}<r<1$ とする。点 $P$ が線分 $OA,~AB,~BC$ 上を動くときに点 $P$ を中心とする半径 $r$ の球（内部を含む）が通過する部分を，それぞれ $V_1, V_2, V_3$ とする。

(1) 平面 $y = t$ が $V_1, V_3$ 双方と共有点をもつような $t$ の範囲を与えよ。さらに，この範囲の $t$ に対し，平面 $y = t$ と $V_1$ の共通部分および平面 $y = t$ と $V_3$ の共通部分を同一平面上に図示せよ。

(2) $V_1$ と $V_3$ の共通部分が $V_2$ に含まれるための $r$ についての条件を求めよ。

(3) $r$ は(2)の条件を満たすとする。 $V_1$ の体積を $S$ とし， $V_1$ と $V_2$ の共通部分の体積を $T$ とする。 $V_1, V_2, V_3$ を合わせて得られる立体 $V$ の体積を $S$ と $T$ を用いて表せ。

(4) ひきつづき $r$ は(2)の条件を満たすとする。 $S$ と $T$ を求め， $V$ の体積を決定せよ。

問題文がちょっと長いですね・・・。最終問題にこの問題があったら遠ざけたくなってしまいます。時間的にもきびしく，2018の本番の試験を受けていた受験生の中でも，この問題の最後までたどり着けた人はほとんどいなかったと思います。

ただ，この問題は六問の中で一番誘導が丁寧であり，腰を据えてじっくり取り組めば，東大受験生であればなんとか答えが出せる問題です。問題自体の難易度が高すぎるというわけではありません。立体の切り口を丁寧に考える練習ができる学習価値の高い問題ですので，しっかり学習しましょう。

まず，(1)です。三次元座標空間の図を書いて，立体を想像しましょう。平面 $y = t$ が $V_1$ と共通部分をもつ範囲，平面 $y = t$ が $V_3$ と共通部分をもつ範囲をそれぞれ独立に考えていきます。断面における2円の半径の大小によって，図示の状況が変わるため，場合分けが必要になることに注意してください。

第六問(1)

第六問立体座標

平面 $y = t$ が $V_1$ と共通部分を持つような $t$ は， $-r \leq t \leq r$ 平面 $y = t$ が $V_3$ と共通部分を持つような $t$ は， $1-r \leq t \leq 1+r$ $\dfrac{1}{2} < r < 1$ より，小さい順に $-r<1-r<r<1+r$ であるから，これらの共通範囲は $1-r \leq t \leq r$ が題意を満たす $t$ の範囲である。

さて， $y = t$ と $V_1$ の共通部分は，ある点 $Q$ が2点 $(0,t,0), (1,t,0)$ による線分上を動く時，点 $Q$ を中心とする半径 $\sqrt{r^2-t^2}$ の $xz$ 平面に平行な円板の通過する部分である。また， $y = t$ と $V_3$ の共通部分は，ある点 $Q$ が2点 $(1,t,0), (1,t,1)$ による線分上を動く時，点 $Q$ を中心とする半径 $\sqrt{r^2-(1-t)^2}$ の $xz$ 平面に平行な円板の通過する部分である。

(i) $y = t$ と $V_1$ の共通部分を形成する円の半径が， $y = t$ と $V_3$ の共通部分を形成する円の半径よりも小さい，つまり $\begin{aligned} \sqrt{r^2-t^2} &\leq \sqrt{r^2-(1-t)^2}\\ r^2-t^2 &\leq r^2-(1-t)^2\\ t &\geq \dfrac{1}{2} \end{aligned}$ のとき，図示すると下図の通り。ただし，平面 $y = t$ と $V_1$ の共通部分は右上向きの斜線，および平面 $y = t$ と $V_3$ の共通部分は右下向きの斜線で表している。

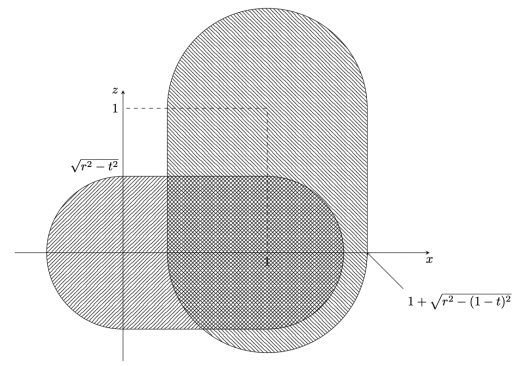
tlarger1/2

(i) $y = t$ と $V_1$ の共通部分を形成する円の半径が， $y = t$ と $V_3$ の共通部分を形成する円の半径よりも大きい，つまり $t \leq \dfrac{1}{2}$ のとき，図示すると下図の通り。ただし，平面 $y = t$ と $V_1$ の共通部分は右上向きの斜線，および平面 $y = t$ と $V_3$ の共通部分は右下向きの斜線で表している。

tsmaller1/2

ただ，本番では，2種類の図を場合分けして書く時間的な余裕はないでしょうし，(2)以降ではこの場合分けは不要ですので，場合分けされていなくてもあまり大きな減点はなかっただろうと予想されます。共通部分がどんな形になるのか想像できることが一番大事です。

続いて(2)です。(1)でせっかく綺麗な図を書いたので，それを利用します。 $y = t$ による $V_2$ の断面は $0 \leq t \leq 1$ の範囲では常に一定の半径 $r$ の円です。 $V_1$ と $V_3$ が共通部分を持つのは $1-r\leq t\leq r$ であるから，この不等式を満たす全ての $t$ に対して， $y = t$ による $V_1$ と $V_3$ の共通部分が， $V_2$ の断面の半径 $r$ の円の内部にあれば良いですね。

これがわかればあとは単純な二次関数の問題です。

第六問(2)

平面 $y = t$ と $V_2$ の共通部分は $xz$ 平面上では， $x = 1, z = 0$ の点を中心とする半径 $r$ の円である。この円の内側に $V_1,V_3$ の共通部分が含まれるという状況が， $1-r\leq t\leq r$ を満たす全ての $t$ で成り立てば良い。

(1) の図より， $xz$ 平面において $V_1,V_3$ の共通部分で $x = 1, z = 0$ の点と最も離れているのは， $\begin{cases} x_{\text{far}} = 1-\sqrt{r^2-(1-t)^2}\\ z_{\text{far}} = \sqrt{r^2-t^2}\\ \end{cases}$ の点であるから， $\sqrt{(1-x_{\text{far}}^2) + z_{\text{far}}^2} \leq r^2$ という不等式が $1-r \leq t \leq r$ を満たすあらゆる $t$ に対して成立していれば良い。この不等式を変形すると， $r^2 - (1-t)^2 + r^2 - t^2 \leq r^2$ $\begin{aligned} r^2 &\leq 2t^2 - 2t + 1\\ &= 2\left(t-\dfrac{1}{2}\right)^2 + \dfrac{1}{2} \end{aligned}$ $1-r \leq t \leq r$ のなかに $t = \dfrac{1}{2}$ は含まれるので， $2\left(t-\dfrac{1}{2}\right)^2 + \dfrac{1}{2}$ の最小値として $t = \dfrac{1}{2}$ のとき $\dfrac{1}{2}$ をとる。よって， $r^2 \leq \dfrac{1}{2}$ であればよく， $\dfrac{1}{2} < r < 1$ と合わせて $\dfrac{1}{2} < r \leq \dfrac{1}{\sqrt{2}}$

(3)は， $V$ の体積を決定するための下準備の問題です。(4)で最終的に求めたい $V$ は $V_1,V_2,V_3$ の「和集合」であると言えますね。3つの集合の和集合ということは， $V$ の体積は， $V_1$ の体積， $V_2$ の体積， $V_3$ の体積の和から， $V_1,V_2$ の共通部分の体積， $V_2,V_3$ の共通部分の体積， $V_3,V_1$ の共通部分の体積の和を引き，最後に $V_1,V_2,V_3$ の共通部分の体積を足せば求めることができます。ベン図を書いてみるとこのことは明らかでしょう。

また，もう二つほどポイントがあります。

まず一つ目です。 $V_1,V_3$ の共通部分は $V_2$ に含まれています。ということは， $V_2 \cap (V_1 \cap V_3)$ というのは $V_1 \cap V_3$ に等しいことがわかります。よくわからなければ，ベン図を書いて確かめてみてください。

そしてもう一つは，対称性です。線分 $OA,~AB,~BC$ 　は長さが等しいので， $V_1,V_2,V_3$ は同じ形です。また， $V_1,V_2$ の共通部分， $V_2,V_3$ の共通部分も対称性から同じ形をしています。

これらのことを踏まえると解答を作ることができます。

第六問(3)

ある立体 $E$ の体積を $\mathrm{Vol}(E)$ として記述することにする。このとき， $\begin{aligned} \mathrm{Vol}(V) = &\mathrm{Vol}(V_1)+\mathrm{Vol}(V_2)+\mathrm{Vol}(V_3)\\ &-\mathrm{Vol}(V_1 \cap V_2)-\mathrm{Vol}(V_2 \cap V_3)-\mathrm{Vol}(V_3 \cap V_1) \\&+ \mathrm{Vol}(V_1 \cap V_2 \cap V_3) \end{aligned}$ ここで， $V_1,V_3$ の共通部分は $V_2$ に含まれているので $\mathrm{Vol}(V_1 \cap V_2 \cap V_3) = \mathrm{Vol}(V_3 \cap V_1)$ また，対称性により $\mathrm{Vol}(V_1)=\mathrm{Vol}(V_2)=\mathrm{Vol}(V_3)=S$ かつ $\mathrm{Vol}(V_1 \cap V_2) = \mathrm{Vol}(V_2 \cap V_3) = T$ が言えるので， $\mathrm{Vol}(V) = 3S -2T$ である。

ここまで完璧にできれば(4)は難しくありません。

$S$ は球と円柱の組み合わせとして考えれば一瞬で求まりますね。 $T$ については $V_1$ かつ $V_2$ の立体を $z = v~~(-r\leq v \leq r)$ で切断してその断面積を考えます。断面積が球の断面積の何倍かを考えれば，積分計算を省略することができます。

第六問(4)

$S$ について，半径 $r$ の球の体積と，半径 $r$ 円を底面にもつ高さ $1$ の円柱の体積を足せばよく， $S = \dfrac{4}{3} \pi r^3 + \pi r^2$ 次に $T$ について考える。 $-r \leq v \leq r$ を満たす $v$ を用いて，平面 $z = v$ で $V_1,V_2$ の共通部分を切った時の断面は以下の斜線部のようになる。 V_1とV_2の共通部分よって，断面の面積は $\left(\sqrt{r^2 - v^2}\right)^2 + \dfrac{3}{4}\times \pi\left(\sqrt{r^2 - v^2}\right)^2\\ = \left(\dfrac{3}{4}\pi + 1\right)(r^2 - v^2)$ $(1,0,0)$ を中心とする半径 $r$ の球を，平面 $z = v$ で切断した時の断面積は $\pi (r^2 - v^2)$ であるから， $V_1,V_2$ の共通部分を切った時の断面積は球の断面積の $\dfrac{\left(\dfrac{3}{4}\pi + 1\right)(r^2 - v^2)}{\pi (r^2 - v^2)} = \dfrac{\dfrac{3}{4}\pi + 1}{\pi}$ 倍である。よって， $T = \dfrac{4}{3} \pi r^3 \times \dfrac{\dfrac{3}{4}\pi + 1}{\pi} = r^3\left(\pi + \dfrac{4}{3}\right)$ これらにより， $\begin{aligned} \mathrm{Vol}(V) &= 3S-2T\\ &= 3\left(\dfrac{4}{3} \pi r^3 + \pi r^2\right)-2r^3\left(\pi + \dfrac{4}{3}\right)\\ &= 2\pi r^3 - \dfrac{8}{3}r^3 + 3\pi r^2 \end{aligned}$

$T$ については上のようにうまくやらなくとも，単に積分して求めても構いません。

第六問(4)別解

共通部分の断面積を求めるところまでは同じ。 $\begin{aligned} T &= \int_{-r}^{r}\left(\dfrac{3}{4}\pi + 1\right)(r^2 - v^2)dv\\ &= \left(\dfrac{3}{4}\pi + 1\right)\cdot 2\left[r^2v - \dfrac{v^3}{3}\right]_0^r\\ &= r^3\left(\pi + \dfrac{4}{3}\right) \end{aligned}$ 以下同様。

長かったですね。お疲れ様でした。

難易度はそんなに高くないことがわかっていただけたと思いますが，これを25分やそこらで完答するのは至難の業でしょう。本番では(1)や(3)を少し拾うくらいで十分すぎるくらいです。ですが，普段の学習ではこういう問題にも触れていろいろな思考の方法を学んで行くと，数学が楽しくなってくると思います。

東大理系数学2018入試過去問解説のまとめ

第五問，第六問は時間内に解き切るのはなかなか難しいでしょう。この二問に関しては，部分点を狙いに小問をちょっと挑戦してみるというのが受験では正しい戦略になると思います。ただ，学習価値は高い問題ですし，他の解き方はないのかなど，いろいろ研究してみるのも楽しいかもしれません。

全体の難易度から考えると，第一問から第四問までをいかに解けるかが鍵になってきます。特に第一問と第四問は理系の東大受験生ならば落としたくない問題と言えるでしょう。

東大数学で満点近くの点数をとってしまうような人たちの思考の速さがどんなにすごいか，今回解説記事を書いてみて身をもって知りました。