計算
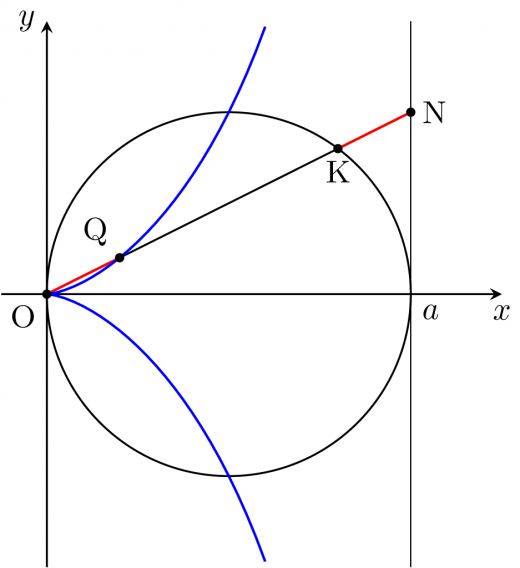
N(a,atanθ)(−2π<θ<2π) と取る。
このとき K(2a+2acos2θ,2asin2θ) となります。
条件より OQ=KN である。
よって,Q(x,y) とすると
(xy)=⎝⎛2a−2acos2θatanθ−2asin2θ⎠⎞
となる。
x=2a−2acos2θ=2a−2a(1−2sin2θ)=asin2θ
と計算される。
よって sin2θ=ax となる。
また
y=atanθ−2asin2θ=cosθasinθ−asinθcosθ=asinθcosθ1−cos2θ=1−sin2θasin3θ=xax1−ax1=xa−xx
となる。
辺々2乗して整理すると
x3+(x−a)y2=0
を得る。