内接円の半径と三角形の面積
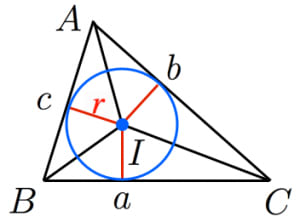
内接円とは,三角形の3つの辺全てに接する円のこと。内接円の半径は, という公式を使って計算できる。
三角形の内接円について解説します。前半では,内接円の半径を計算する方法を解説し,後半では公式を2通りの方法で証明します。
内接円とは
内接円とは
三角形が与えられたときに,3つの辺全てに接する円のことを内接円と言います。また,内接円の中心を内心と言います。
この記事では,以下のような「内接円の半径を求める問題」について詳しく解説します。
三辺の長さが である三角形 の内接円の半径を求めよ。
内接円の半径を計算する公式
内接円の半径を計算する公式
内接円の半径 を計算する問題では, という公式を使います。
ただし, は三角形の三辺の長さで, は面積です。
さきほどの例題1を解いてみましょう。
実は,三角形 は直角三角形である。実際, であり,三平方の定理の逆から直角三角形であることが分かる。
したがって,面積は
よって,内接円の半径を とすると,公式より
よって,
このように,三角形の三辺の長さと面積が分かれば内接円の半径も分かります。
一般の三角形の内接円の半径
一般の三角形の内接円の半径
例題1は直角三角形でしたが,直角三角形でない場合も内接円の半径を計算する場合には,同じ公式 を使います。
三辺の長さが である三角形の内接円の半径を求めよ。
公式の証明1
公式の証明1
内接円の半径を計算する公式 を2通りの方法で証明します。まずは,多くの参考書に載っている有名な証明方法です。
三角形 の面積を などと書きます。

内接円の中心を とおくと,
ここで,,, より,
三角形を,内心を使って3つに分けて,それぞれの面積を計算するというテクニックです。非常に重要なテクニックなので,覚えることをおすすめします。
公式の証明2
公式の証明2
内接円の半径の公式を証明する方法は他にもあります。証明1に比べて計算も大変で筋が悪いですが,全てを で表すという方針でも証明できます。
- ヘロンの公式より,
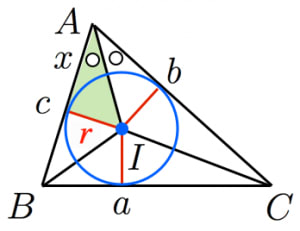
- 図において
ここで
より であり,
以上より
二つの式から となり,公式は証明された。
なお,傍心に関しても似たような公式が成立します。→傍心の意味と性質・内心との比較
面積を用いない方法
面積を用いない方法
直角三角形の場合,面積を用いないで内接円の半径を求めることもできます。
三辺の長さが である三角形 の内接円の半径を求めよ。
図のように記号を定める。 は接点。
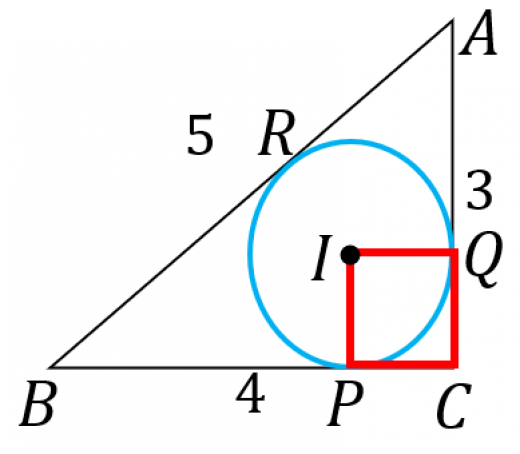
が直角であることなどから, は1辺の長さが の正方形になる。1辺の長さは内接円の半径 である。
さらに,同じ点から引いた2本の接線の長さは等しいので
よって,,
面積で考える方法も,接線の長さで考える方法も,どちらも同じくらい楽しいです。











