傍心の意味と性質・内心との比較

更新 2022/01/24

三角形の傍心の意味と性質を整理しました。三角形の内心と比較しながらわかりやすく説明します。

傍心とは

傍心の定義

傍心の定義任意の三角形について，1つの内角の二等分線と，残り2つの外角の二等分線は1点で交わる。この点を傍心と言う。

図では， $\angle A$ の内角と，残り2つ $B,C$ の外角の二等分線の交点を表しています。 $A$ に対する傍心と呼ぶことにします。
傍心はぼうしんと読みます。
3つの頂点のうちどの内角を選ぶかによって点が変わります。つまり，傍心は「 $A$ に対する傍心」「 $B$ に対する傍心」「 $C$ に対する傍心」の3つあります。

参考：三角形の五心の覚えておくべき性質まとめ

傍心が存在することの証明

まずは，傍心が存在することを証明します。つまり「1つの内角の二等分線と，残り2つの外角の二等分線は1点で交わる」を証明します。

証明

$B$ と $C$ の外角の二等分線の交点を $I_A$ とおく。 $I_A$ から $BC,CA,AB$ におろした垂線の足を $D,E,F$ とする。

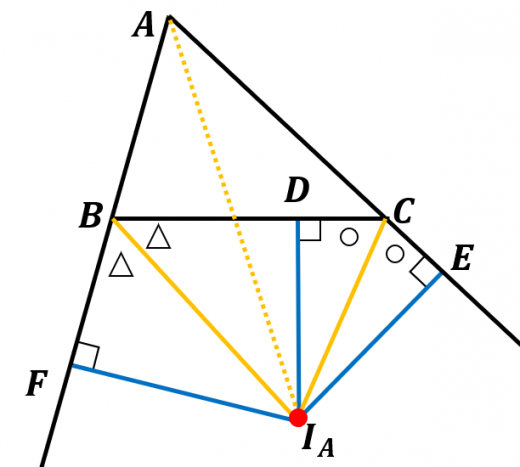
傍心の存在証明

三角形 $BFI_A$ と $BDI_A$ は合同（直角三角形で斜辺と1つの角がそれぞれ等しい）なので $I_AF=I_AD$
三角形 $CDI_A$ と $CEI_A$ は合同なので $I_AD=I_AE$

以上より $I_AF=I_AE$

よって，三角形 $AFI_A$ と $AEI_A$ は合同（直角三角形で斜辺ともう1辺がそれぞれ等しい）なので $I_A$ は $\angle A$ の二等分線上にある。

傍心と内心

傍心の定義は，以下の内心の定義と似ています！

内心の定義

任意の三角形について，3つの内角の二等分線は1点で交わる。この点を内心と言う。

実は，傍心に関する性質は内心に関する性質とほとんど同じです。内心でできることは傍心でもできて，内心でできないことは傍心にもできません。というわけで，以下では内心の性質と比較しながら傍心の性質を紹介していきます。

傍接円の半径

$A$ に対する傍心 $I_A$ について考えます。 $I_A$ は，直線 $AB,BC,CA$ までの距離が等しいです。つまり，傍心を中心として3つの直線に接する円が書けます。これを傍接円と言います。傍接円の半径を $r_A$ とすると，以下が成立します。

傍接円の半径

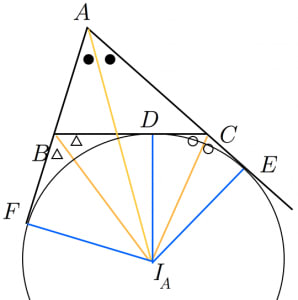
傍心の性質

$S=\dfrac{1}{2}r_A(-a+b+c)=r_A(s-a)$

ただし， $S$ は三角形 $ABC$ の面積， $a=BC,b=CA,c=AB$ で $s=\dfrac{a+b+c}{2}$ です。これは，内接円の半径 $r$ に関する公式
$S=\dfrac{1}{2}r(a+b+c)=rs$
と似ています！→内接円の半径と三角形の面積

証明

内接円の場合，面積について

△ $ABC$ =△ $IBC$ +△ $ICA$ +△ $IAB$

が成り立つことから $S=\dfrac{1}{2}r(a+b+c)$ がわかった。

傍接円の場合も同様に，面積について

△ $ABC$ =ー△ $I_ABC$ +△ $I_ACA$ +△ $I_AAB$

が成り立つことから $S=\dfrac{1}{2}r_A(-a+b+c)$ がわかる。

傍接円の接点までの距離

次は，三角形の頂点と「傍接円の接点 $D,E,F$ 」までの距離について考えます。

傍接円の接点までの距離

傍心の性質

$AE=AF=\dfrac{1}{2}(a+b+c)=s$
$BF=BD=\dfrac{1}{2}(a+b-c)=s-c$
$CD=CE=\dfrac{1}{2}(a-b+c)=s-b$

これは，内接円の接点までの距離についての公式と似ています！：内接円の性質

$AF=AE=\dfrac{1}{2}(-a+b+c)=s-a$
$BF=BD=\dfrac{1}{2}(a-b+c)=s-b$
$CD=CE=\dfrac{1}{2}(a+b-c)=s-c$

証明

内心の場合の公式は，「1点から円に引いた2本の接線の長さが等しい」という性質：
$AF=AE, BD=BF, CD=CE$
から導出できた。(詳細は，タンジェントの美しい関係式の後半参照)

傍心の場合も同じく
$AF=AE, BD=BF, CD=CE$
は成立し，以下のように証明できる：傍心の性質

$AF=c+BF\\ =c+BD\\ =c+a-CD\\ =a+c-CE\\ =a+c-(AE-b)\\ =a+b+c-AF$

よって， $AF=\dfrac{1}{2}(a+b+c)$

他の辺に関しても同様。

このように傍心は内心と同様に扱えます。内心に関する性質は導出方法も含めて覚えておくべきですが，傍心に関する性質は覚える必要はありません。傍心の性質は内心の場合から導出できますので。

4つの円の半径と三角形の面積

最後に，内接円と傍接円に関するおもしろい定理を紹介します。

定理

内接円の半径 $r$ と3つの傍接円の半径 $r_A,r_B,r_C$ に対して，

$S=\sqrt{rr_Ar_Br_C}$

証明

「傍接円の半径」のところで紹介した式を並べる。

$S=rs$
$S=r_A(s-a)=r_B(s-b)=r_C(s-c)$

これと，ヘロンの公式：

$S^2=s(s-a)(s-b)(s-c)$

から分かる。

三角形の五心というけれど，本質的には四心

Tag:三角形の五心に関する定理まとめ

Tag:三角形の面積を求める公式まとめ

Tag:数学Aの教科書に載っている公式の解説一覧

この記事の監修者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！