三角形の五心に関する定理まとめ

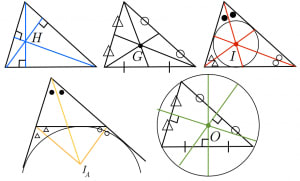
1：三角形の五心の覚えておくべき性質を整理

三角形の五心の定義と頭に入れておくべき基本的な性質をまとめました。それぞれの中心の位置ベクトル表示も示しています。

2：傍心の意味と性質・内心との比較

内心と傍心はほぼ同様に扱えることを解説します。内接円と傍接円の半径と面積の関係，接線の長さのお話。

3：オイラー線の3通りの証明

外心，重心，垂心にまつわる美しい定理の紹介。初等幾何好きならぜひしっておいて欲しい定理です。

4：オイラーの定理（初等幾何）

外心と内心の距離を外接円の半径と内接円の半径のみで表す美しい定理。

5：三角形の五心と頂点までの距離

個人的に垂心と頂点の距離がお気に入りです。

実は，三角形は五心以外にも5000種類以上の中心が存在します。

詳しくはEncyclopedia of Triangle Centers参照。

代表的なものをいくつか紹介していきます。

・フェルマー点

6：三角形のフェルマー点の3通りの証明

頂点からの距離の和を最小にする点をフェルマー点といいます。工学的にも重要な意味を持っています。特に2番めの証明方法がおすすめです。

・ジュルゴンヌ点，ナーゲル点

7：ジュルゴンヌ点とナーゲル点の存在証明

・ルモアーヌ点

8：ルモアーヌ点（類似重心）とその性質