三角形の面積のベクトル・成分を用いた公式

更新 2022/07/26

$\overrightarrow{OA} = \overrightarrow{\vphantom{b}a} = \begin{pmatrix} a_1\\ a_2 \end{pmatrix}, ~ \overrightarrow{OB} = \overrightarrow{b} = \begin{pmatrix} b_1\\ b_2 \end{pmatrix}$ としたとき，三角形 $OAB$ の面積 $S$ は以下のように表せる。

$S = \dfrac{1}{2}\sqrt{\|\overrightarrow{\vphantom{b}a}\|^2\|\overrightarrow{b}\|^2 - \left(\overrightarrow{\vphantom{b}a} \cdot \overrightarrow{b}\right)^2}\tag{1}$ $S = \dfrac{1}{2}| a_1b_2 - a_2b_1| \tag{2}$

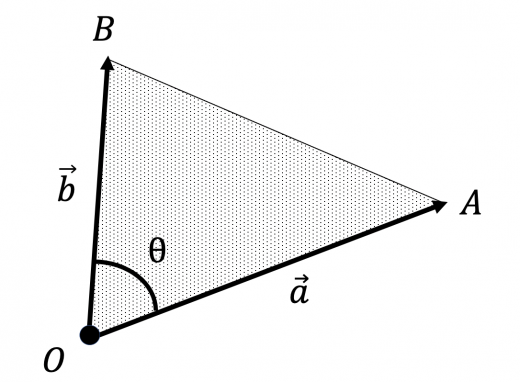
三角形OAB

ベクトルや座標平面上に表された三角形の面積を表す公式について，証明とその利用例を解説します。

三角形の面積の公式の確認

三角形 OABOABOAB において，∠AOB=θ\angle AOB = \theta∠AOB=θ とすると，三角形 OABOABOAB の面積 SSS は，
S=12∥baundefined∥∥bundefined∥sin⁡θ
S = \dfrac{1}{2}\|\overrightarrow{\vphantom{b}a}\|\|\overrightarrow{b}\|\sin\theta
S=21​∥ba∥∥b∥sinθ
で表されます。この公式については以下の記事で解説しています。→sinを用いた三角形の面積公式
冒頭の公式 (1)(1)(1)  (2)(2)(2) の証明には，この公式を使います。

三角形の面積のベクトル表示

では早速式 $(1)$ から証明してみます。

(1)の証明

内積の定義 $\overrightarrow{\vphantom{b}a}\cdot\overrightarrow{b} = \|\overrightarrow{\vphantom{b}a}\|\|\overrightarrow{b}\| \cos \theta$ により， $\cos \theta = \dfrac{\overrightarrow{\vphantom{b}a}\cdot\overrightarrow{b}}{\|\overrightarrow{\vphantom{b}a}\|\|\overrightarrow{b}\|}$ $\sin \theta > 0$ より，三角関数の相互関係（詳しくは三角関数の相互関係とその証明をご覧ください）： $\sin^2{\theta}+\cos^2{\theta} =1$ を用いて $\begin{aligned} \sin \theta &= \sqrt{1-\cos^2 \theta}\\ &= \sqrt{1-\left(\dfrac{\overrightarrow{\vphantom{b}a}\cdot\overrightarrow{b}}{\|\overrightarrow{\vphantom{b}a}\|\|\overrightarrow{b}\|}\right)^2} \end{aligned}$ よって，三角形の面積は $\begin{aligned} S &= \dfrac{1}{2}\|\overrightarrow{\vphantom{b}a}\|\|\overrightarrow{b}\|\sin\theta\\ &= \dfrac{1}{2}\|\overrightarrow{\vphantom{b}a}\|\|\overrightarrow{b}\|\sqrt{1-\left(\dfrac{\overrightarrow{\vphantom{b}a}\cdot\overrightarrow{b}}{\|\overrightarrow{\vphantom{b}a}\|\|\overrightarrow{b}\|}\right)^2}\\ &= \dfrac{1}{2}\sqrt{\|\overrightarrow{\vphantom{b}a}\|^2\|\overrightarrow{b}\|^2 - \left(\overrightarrow{\vphantom{b}a} \cdot \overrightarrow{b}\right)^2} \end{aligned}$

やや複雑な形をしていますが，使える機会が多いので正確に覚えておきましょう。

三角形の面積の成分表示　〜座標を用いた証明〜

式 $(2)$ は，サラスの公式でも登場する有名な式です。

上記の記事には式 $(1)$ を利用した証明が書かれています。ここでは別の証明方法を紹介します。

(2)の証明

サラスの公式証明

$B$ から辺 $OA$ に向かって垂線を引き，その垂線の足を $H$ とする。

$a_1 \neq 0$ のとき

直線 $OA$ の方程式は $y = \dfrac{a_2}{a_1}x$ で表される。この直線と $B$ との距離 $d$ は，点と直線の距離の公式より， $d = \dfrac{\left|\dfrac{a_2}{a_1}b_1 - b_2\right|}{\sqrt{\dfrac{a_2^2}{a_1^2} + 1}} = \dfrac{|a_2b_1 - a_1b_2|}{\sqrt{a_1^2 + a_2^2}}$ 辺 $OA$ の長さは $\sqrt{a_1^2 + a_2^2}$ であるから， $\begin{aligned} S &= \dfrac{1}{2} \sqrt{a_1^2 + a_2^2} \cdot \dfrac{|a_2b_1 - a_1b_2|}{\sqrt{a_1^2 + a_2^2}}\\ &= \dfrac{1}{2}|a_2b_1 - a_1b_2|\\ &= \dfrac{1}{2}|a_1b_2 - a_2b_1|\\ \end{aligned}$

$a_1 = 0$ のとき

直線 $OA$ の方程式は $x = 0$ で表される。この直線と $B$ との距離は $|b_1|$ であり， $OA = |a_2|$ であるから， $S = \dfrac{1}{2}|a_2b_1|$

どちらの場合も式 $(2)$ が成立。

証明では点と直線の距離の公式を利用しました（→点と直線の距離公式：例題と5通りの証明）。

問題例

公式を利用できる簡単な問題を解いてみます。

例1

$\|\overrightarrow{AB}\| = 4, ~\|\overrightarrow{AC}\| = 3, ~\overrightarrow{AB}\cdot \overrightarrow{AC} = 8$ を満たす三角形 $ABC$ の面積を求めよ。

公式 $(1)$ を利用するだけです。求めたい三角形の面積を $S$ とすると， $\begin{aligned} S &= \dfrac{1}{2}\sqrt{4^2 \cdot 3^2 - 8^2}\\ &= \dfrac{1}{2} \sqrt{144-64}\\ &= \dfrac{1}{2} \cdot 4\sqrt{5}\\ &= 2\sqrt{5} \end{aligned}$ と求めることができます。

例2

座標平面上に $A(0,0), B(2,-1), C(5,4)$ があるとき，三角形 $ABC$ の面積を求めよ。

点が座標で表されているので，公式 $(2)$ を利用するのが良さそうです。求めたい三角形の面積を $S$ とすると， $\begin{aligned} S &= \dfrac{1}{2}|2\cdot 4 - (-1)\cdot 5|\\ &= \dfrac{1}{2}|8 + 5|\\ &= \dfrac{13}{2} \end{aligned}$ と求めることができます。

例3

座標平面上に $A(2,4), B(4,-3), C(-1,0)$ があるとき，三角形 $ABC$ の面積を求めよ。

この問題には2通りのやり方を紹介します。

まず，公式 $(1)$ を利用する方法です。 $\overrightarrow{AB} = \left( \begin{array}{c} 2\\ -7 \end{array} \right), ~\overrightarrow{AC} = \left( \begin{array}{c} -3\\ -4 \end{array}\right)$ ですから，これを使って計算します。 $\begin{aligned} \|\overrightarrow{AB}\|^2 &= 2^2 + (-7)^2 = 53\\ \|\overrightarrow{AC}\|^2 &= (-3)^2 + (-4)^2 = 25\\ \overrightarrow{AB}\cdot\overrightarrow{AC} &= -6 + 28 = 22 \end{aligned}$ により，求めたい三角形の面積を $S$ とすると， $\begin{aligned} S &= \dfrac{1}{2}\sqrt{53 \cdot 25 - 22^2}\\ &= \dfrac{1}{2} \sqrt{1325-484}\\ &= \dfrac{1}{2} \cdot \sqrt{841}\\ &= \dfrac{29}{2} \end{aligned}$ と求めることができます。

次に，公式 $(2)$ を利用するやり方です。原点に一致する点がないので，公式を利用することができないと思うかもしれません。

しかし，三点を同じ方向同じ距離だけ平行移動しても三角形の面積は変わりません。そこで，どれか一点が原点に重なるように平行移動することを考えましょう。

今回は $C$ を $(0,0)$ に一致させる，つまり $x$ 方向に $+1$ 平行移動することを考えます。

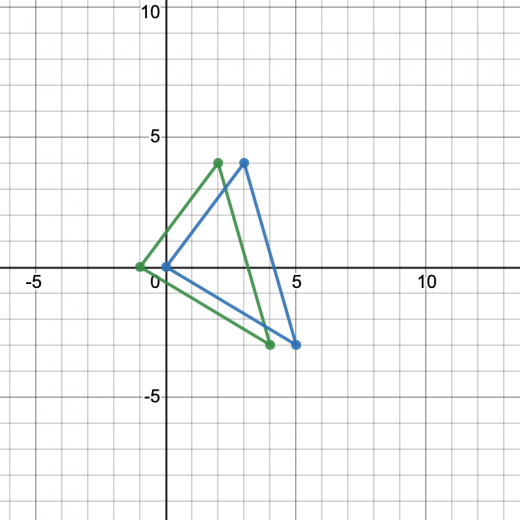
平行移動した三角形

このとき $A$ は $A'(3,4)$ ， $B$ は $B'(5,-3)$ に移動します。求めたい三角形の面積は，三角形 $OA'B'$ に一致するので， $\begin{aligned} S &= \dfrac{1}{2}|3\cdot(-3) - 5\cdot 4|\\ &= \dfrac{29}{2} \end{aligned}$ と求めることができます。

平行四辺形も同様の公式で求められる

合同な三角形を二つ繋げると平行四辺形になるので，上記の公式から 12\dfrac{1}{2}21​ を取った式で平行四辺形の面積を求めることができます。
OAundefined=baundefined=(a1a2), OBundefined=bundefined=(b1b2)\overrightarrow{OA} = \overrightarrow{\vphantom{b}a} = 
\begin{pmatrix}
a_1\\
a_2
\end{pmatrix}, ~
\overrightarrow{OB} = \overrightarrow{b} = 
\begin{pmatrix}
b_1\\
b_2
\end{pmatrix}OA=ba=(a1​a2​​), OB=b=(b1​b2​​)
 としたとき，平行四辺形 OACBOACBOACB の面積 S′S'S′ は以下のように表せます。
S′=∥baundefined∥2∥bundefined∥2−(baundefined⋅bundefined)2(3)
S' = \sqrt{\|\overrightarrow{\vphantom{b}a}\|^2\|\overrightarrow{b}\|^2 - \left(\overrightarrow{\vphantom{b}a} \cdot \overrightarrow{b}\right)^2} \tag{3}S′=∥ba∥2∥b∥2−(ba⋅b)2​(3)
S′=∣a1b2−a2b1∣(4)S' = | a_1b_2 - a_2b_1| \tag{4}S′=∣a1​b2​−a2​b1​∣(4)

これも知っていると計算が楽になることが多いので，合わせて覚えておきましょう。

【補足】3次元の場合の三角形の面積のベクトル表示

3次元の場合にも，空間ベクトルを用いて三角形 $OAB$ の面積を求めることができます。

$\overrightarrow{OA} = \overrightarrow{\vphantom{b}a} = \begin{pmatrix} a_1\\ a_2\\ a_3 \end{pmatrix}, ~ \overrightarrow{OB} = \overrightarrow{b} = \begin{pmatrix} b_1\\ b_2\\ b_3 \end{pmatrix}$ としたとき，三角形 $OAB$ の面積 $S$ は以下のように表せる。

$S = \dfrac{1}{2}\sqrt{\|\overrightarrow{\vphantom{b}a}\|^2\|\overrightarrow{b}\|^2 - \left(\overrightarrow{\vphantom{b}a} \cdot \overrightarrow{b}\right)^2}$
$\begin{aligned} S = \dfrac{1}{2} \sqrt{(a_2b_3-a_3b_2)^2 + (a_3b_1-b_3a_1)^2 + ( a_1b_2 - a_2b_1)^2 } \end{aligned}$

1つめの証明は2次元の場合と同じです。さらに，1つめに空間ベクトルを成分表示して代入すると，2つめが導出できます。

この公式は外積という概念と繋がっています。詳しくはベクトルの内積と外積の意味と嬉しさをチェックしてみてください。

少し複雑な公式に見えますが，何回か使っていればすぐに覚えられると思います。

この記事の監修者

でーちー

公立地方進学校出身。高校時代は部活動に勤しみ，合間を縫って勉強を進めた。受験生時代には毎日12時間以上の勉強を続け，東京大学理科一類に現役合格。大学でも数学・物理を得意とし，情報系の学科に進みつつも，独学で勉強を続けている。学びTimesでは主に「高校数学の美しい物語」「高校生から味わう理論物理入門」の記事執筆・修正業務に尽力している。