外接円の半径と内接円の半径の関係
三角形 の内接円の半径を , 外接円の半径を とするとき,
- (オイラーの不等式)
どちらも美しい関係式です,数学オリンピックをめざす人は覚えておきましょう。
1の証明を3通り紹介します。後半では1の結果を使って2を証明します。
1の証明(三角関数の計算による方法)
1の証明(三角関数の計算による方法)
内接円の半径と面積の関係式から, 外接円の半径と面積の関係式から, 2つの式から を消去すると, ここで,正弦定理を用いて辺の情報を角度の情報に変換する: 左辺を倍角公式,右辺を和積公式の発展版で変形する: この式を整理して求める公式を得る。
1の証明(図形的な考察による方法)
1の証明(図形的な考察による方法)
証明2は比較的自然です。
内接円と の接点を とおく。
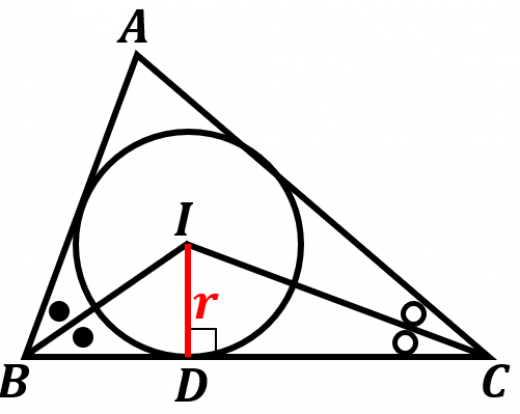 である。一方,正弦定理より
以上より
左辺にサインの倍角公式を使って分母を払うと
となり で割ると目標の式を得る。
である。一方,正弦定理より
以上より
左辺にサインの倍角公式を使って分母を払うと
となり で割ると目標の式を得る。
証明3は思いつくのがかなり難しいです。

まず,強引に と を登場させる。
三角形の内心を とおくと, 次に,強引に と を登場させる。
直線 と外接円の交点を とおく。
三角形 に正弦定理を用いて,
以上2式から,
目的の式と比較すると,
を示せばよいが,
これは より従う。
オイラーの不等式の証明
オイラーの不等式の証明
公式1を用いてオイラーの不等式()を証明します。
ちなみに,等号成立条件は ,つまり三角形 が正三角形の場合であるということも分かります。
三角関数による自然な証明も図形的な考察による証明もどちらもおもしろいです。
Tag:幾何不等式の解法パターンまとめ











