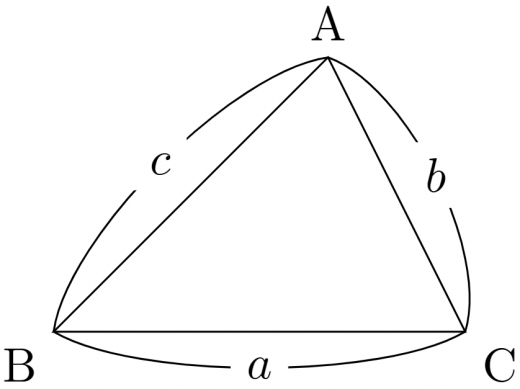
4通りの証明を紹介します。
垂線を下ろす証明
証明1
A から BC に垂線 AH をおろす。B≦90∘ の場合を考える。

BH=ccosB
CH=a−ccosB
三角形 AHB と AHC に三平方の定理を使うと,
AH2AH2=AB2−BH2=c2−(ccosB)2=AC2−CH2=b2−(a−ccosB)2
上の2つの式から
c2−(ccosB)2=b2−(a−ccosB)2
これを整理すると
a2+c2−2accosB=b2
となり余弦定理を得る。
B>90∘ の場合も図が少し変わるがほぼ同様。
第一余弦定理を使う証明
実は余弦定理には2種類あります。
以下の証明2と証明3では「第一余弦定理」を使います。
証明2
第一余弦定理:a=bcosC+ccosB より,
a2=a×a=a(bcosC+ccosB)=b×acosC+c×acosB
第一項に第一余弦定理 b=acosC+ccosA を使い,
第二項に第一余弦定理 c=acosB+bcosA を使うと
a2=b(b−ccosA)+c(c−bcosA)=b2+c2−2bccosA
証明3
一般の三角形に対して b2+c2−2bccosA=a2 を示す。
第一余弦定理より a=bcosC+ccosB が成り立つ。この両辺を2乗すると,
a2=(bcosC+ccosB)2=b2cos2C+c2cos2B+2bccosBcosC⋯∗
が得られる。
sin2θ+cos2θ=1 を用いると,
∗=b2(1−sin2C)+c2(1−sin2B)+2bccosBcosC=b2+c2+2bccosBcosC−b2sin2C−c2sin2B+2bc(sinBsinC−sinBsinC)=b2+c2+2bccosBcosC−2bcsinBsinC−b2sin2C−c2sin2B+2bcsinBsinC=b2+c2−(bsinC−csinB)2+2bc(cosBcosC−sinBsinC)⋯∗∗
と変形できる。
三角形 ABC の面積を S をおくと,
S=21absinC=21acsinB
である。こうして bsinC=csinB を得る。
また,加法定理を用いることで
cosBcosC−sinBsinC=cos(B+C)
となる。A,B,C は三角形の内角であったため,A+B+C=π である。ゆえに cos(B+C)=cos(π−A)=−cosA である。
上記をまとめると,
∗∗=b2+c2+2bccos(B+C)=b2+c2+2bccos(π−A)=b2+c2−2bccosA
ベクトルによる証明