方べきの定理の意味と2通りの証明
更新
方べきの定理の意味と証明 を3パターンそれぞれ解説します。最後に,3パターンを統一的に証明します。
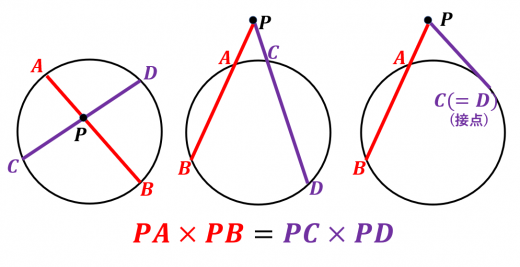
方べきの定理タイプ1とその証明
方べきの定理タイプ1とその証明
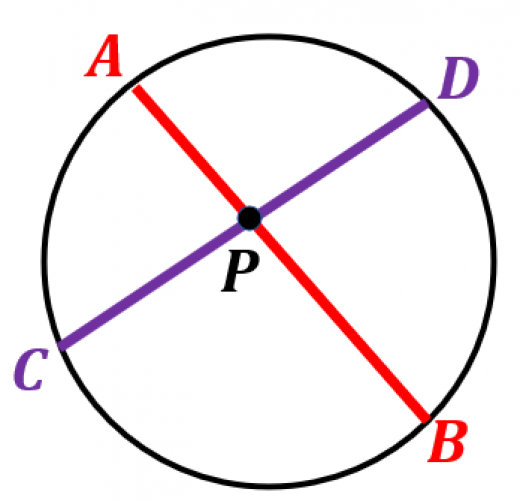
円周上に点 がある。 と が 円の内部の点 で交わるとき,
円周角の定理より,

よって,2組の角がそれぞれ等しいので,三角形 と は相似。
よって, となり,方べきの定理が成立する。
方べきの定理タイプ2とその証明
方べきの定理タイプ2とその証明

円周上に点 がある。 と が 円の外部の点 で交わるとき,
タイプ1では点 が円の内側にありましたが,タイプ2では点 が円の外側にあります。
方べきの定理タイプ3とその証明
方べきの定理タイプ3とその証明

円周上に点 がある。直線 と における接線が で交わるとき,
方べきの定理を統一的に見る
方べきの定理を統一的に見る
- 3タイプの図を並べてみると「似ている」と感じる人もいるでしょう。

-
タイプ3において接線をほんの少し内側にずらすと円と二点で交わることになるのでタイプ2になります。つまりタイプ3はタイプ2の極限と見ることができます。
-
3タイプとも,証明には三角形の相似を使いました。相似を導くのに使った道具は「円周角の定理」「内接四角形の性質」「接弦定理」と異なりました。
-
実は,座標を用いることで3タイプ同時に方べきの定理を証明できます!
座標を用いた方べきの定理の証明
座標を用いた方べきの定理の証明
方べきの定理を直交座標における計算で証明します。
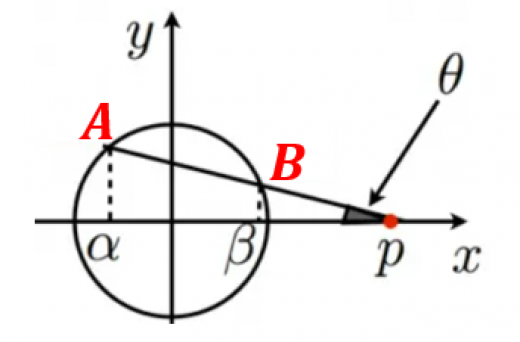
円 ,点 としても一般性を失いません。点 を通る直線 は傾き を用いて
と書け,このとき と の交点を とおきます(交点が1つのときは )。
が によらないことを示せばOKです。
と の方程式から を消去すると,
の 座標を とおくと
解と係数の関係より
また,上図のように と 軸がなす角を とおくと,
より,
となり傾き によらない!
よって,方べきの定理は成立する。
- 実は座標設定の際に としても一般性を失いませんが,計算の手間は変わりません。
- のときタイプ1, で交点が2つのときタイプ2,また となる場合も考慮できているのでタイプ3も証明できています。
このように,初等幾何では場合分けが必要でも,座標で考えれば統一的に証明できる場合があります。
座標設定の方法,傾きと の話,解と係数の関係など座標計算で重要なテクニックが凝縮されており,非常にためになる証明方法でした。
方べきの定理の場合は,初等幾何による証明が非常に簡単なので座標のありがたみが半減ですが,複数のパターンを統一的に扱うという意識は重要です。
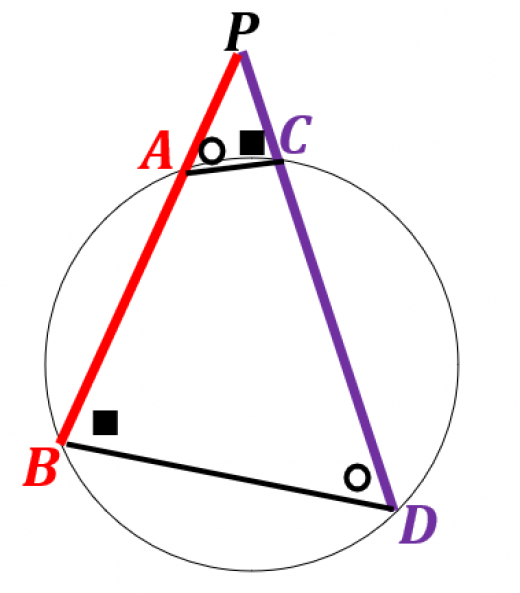 よって,2組の角がそれぞれ等しいので,
よって,2組の角がそれぞれ等しいので,
 よって,2組の角がそれぞれ等しいので,
よって,2組の角がそれぞれ等しいので,










