接弦定理の意味・例題・証明・逆をわかりやすく
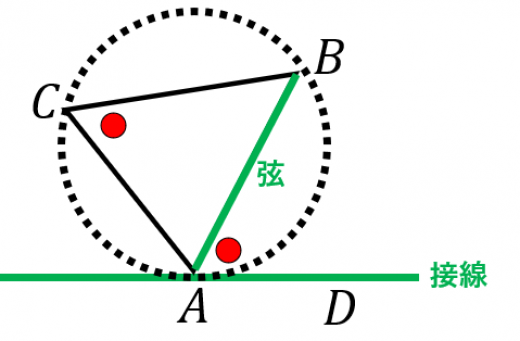
接線と弦のつくる角 は,その弦に対する円周角 と等しい。これを 接弦定理(せつげんていり) と言う。
接弦定理の意味・例題・証明をわかりやすく説明します。後半では接弦定理の逆についても紹介します。
接弦定理を使う問題
接弦定理を使う問題
「接線」と「弦」が作る角度が表れたら,接弦定理を思い出しましょう。
図において,, であるとき, を計算せよ。
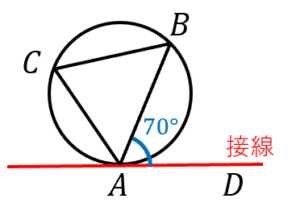
接弦定理より,
また,三角形 は二等辺三角形なので,
以上より,
接弦定理の証明
接弦定理の証明
接弦定理の証明は場合分けが必要なのでやや長いですが,1つ1つは難しくありません。
が鋭角の場合,直角の場合,鈍角の場合の3つに場合分けをして証明します。
接点を ,弦を ,円周角を とします。また,接線上に点 と直線 に関して反対側に点 を適当に取ります。 目標は を証明することです。
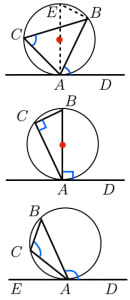
~ が鋭角の場合(上の図)~
が直径となるように点 を取る。
は接線より
また, は直径なので
以上より
これと円周角の定理: より接弦定理が証明された。
~ が直角の場合(真ん中の図)~
は円の直径なので
よって
~ が鈍角の場合(下の図)~
接線上に に関して と反対側に点 を取る。
鋭角の場合の接弦定理(もう証明した)より
よって,
円周角の定理の極限
円周角の定理の極限
次に,接弦定理が成り立つことの感覚的な説明を紹介します。
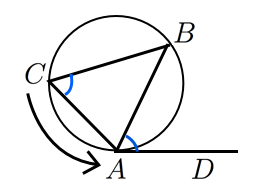
点 を円周上で限りなく に近づけていくと,
-
円周角の定理より は一定
-
直線 は円の接線に近づく
以上から接弦定理が成り立つことが納得できます。
接弦定理の逆
接弦定理の逆
接弦定理の逆は入試ではあまり見かけませんが,数学オリンピックの図形の証明問題では頻出です。
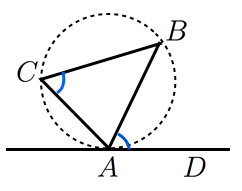
と が直線 に関して反対側にあり, なら直線 は三角形 の外接円と接する。
接弦定理からほぼ明らかですが,一応証明しておきます。
三角形 の外接円の点 における接線上に, に関して と反対側に点 を適当に取る。
接弦定理より である。
これと定理の仮定から
は に関して同じ側にあるので は一直線上にある。つまり直線 は円の接線である。
「接弦定理」というネーミングはなかなか良いと思います。











