単項式，多項式，整式

更新日時 2023/05/06

単項式，多項式，整式という用語について整理しました。

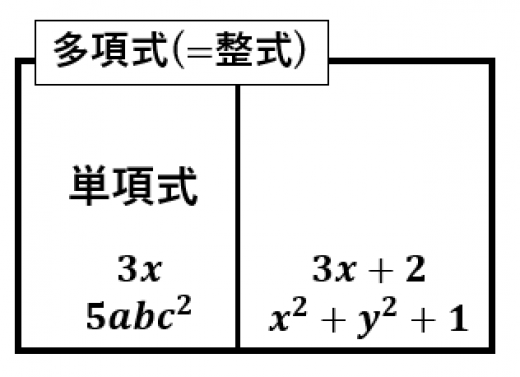
単項式とは

単項式とは，数，文字，およびそれらの積として表される式のこと。

単項式の例

積（かけ算）のみというのが重要です。 $x-y$ や $\dfrac{x}{y}$ は単項式ではありません。

単項式にある文字が含まれているとき，単項式の数の部分を係数といいます。

単項式の係数の例

単項式において，かけられている文字の個数を次数と言います。複数の文字がかけられているときは，かけられている文字全ての個数を数えます。

単項式の次数の例

整式の定義

整式とは，単項式の1つ以上の和として表される式。

多項式の定義

多項式とは，整式のこと。つまり，単項式の1つ以上の和として表される式。

多項式の例

多項式の話は大学以降でも登場します。例えば多項式全体の集合を多項式環と呼びます。各成分が多項式であるような行列を多項式行列と言います。

多項式の定義は上記のものが一般的ですが，整式のうち単項式ではないもののみを多項式と呼ぶ文献も存在します。この定義に基づくと例えば $3x$ は多項式ではありません。

多項式では，含まれる単項式(項)をその次数に従って並び替えることがあります。

項の次数が大きいものから順に並べる並べ方を降べきの順，逆に次数が小さいものから順に並べる並べ方を昇べきの順と言います。

以下は，多項式・整式と間違えやすいけど多項式でないものです。

$\dfrac{1}{x}$ は「数，文字，およびそれらの積として表される式」ではないので整式（単項式）ではありません。ちなみに，整式÷整式で表せる式を有理式，または分数式と言います。 $\dfrac{1}{x}$ は有理式です。
$x^{\frac{1}{2}}=\sqrt{x}$ も同様に整式ではありません。
$\displaystyle\sum_{n=0}^{\infty}x^n=1+x+x^2+\cdots$ のように項が無限個あるようなものも多項式とは言いません（べき級数と言う）。

「整式」は高校数学の一番最初（四月病により勉強のモチベーションが高い時期）に習う内容です。

この記事の編集者

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！