平方完成のやり方といくつかの発展形
=
のように,二次式を の形に変形することを平方完成と言う。

平方完成は,二次方程式の解の公式の導出や,二次関数のグラフを描くときに使う重要な式変形です。
平方完成のやり方を基礎から説明します。
平方完成の意味とやり方
平方完成の意味とやり方
平方完成とは
=
のように,二次式を の形に変形することを平方完成と言います。
右辺から左辺への変形は展開するだけですが,今回は左辺から右辺への変形が目標です。
平方完成の仕方
平方完成は4ステップでできます。例題を見てみましょう。
を平方完成せよ。
-
の係数で の項までくくる:
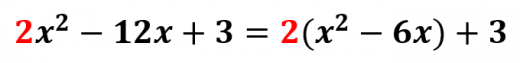
-
の係数の半分の2乗を足して引く。この場合は の半分である の2乗である を足して引く:
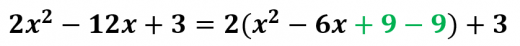
-
カッコの中身の前半を因数分解する:
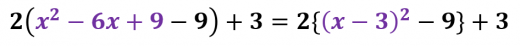
- 定数項を計算する
 ※ と計算した。
※ と計算した。
手順2が一番むずかしいです。いきなり9が登場する部分です。登場するのは「 の係数の半分の2乗」です。
手順3では という因数分解公式を使っています。因数分解の公式とテクニック一覧 のレベル1で詳しく解説しています。
上記の4手順をもう一度まとめます。
- の係数で の項までくくる
- の係数の半分の2乗を足して引く
- カッコの中身の前半を因数分解して2乗の形を作る
- 定数項を計算する
※途中経過をすべて解答に書く必要はありません。平方完成は慣れが重要です。
分数が登場するパターン
分数が登場するパターン
を平方完成せよ。
-
の係数で の項までくくる:
-
の係数の半分の2乗を足して引く。この場合は の半分である の2乗である を足して引く:
-
カッコの中身の前半を因数分解する:
-
定数項を計算する
より答えは
ここまではていねいに解説しましたが,慣れれば の を決める→ を決めるという流れでサクッと計算できます。
右辺の一次の係数が となるように を定めると,
次に定数項を比較すると より
よって,答えは
がマイナスのパターン
がマイナスのパターン
を平方完成せよ。
方針は全く同じ。まず を決める:
(一次の係数は となり一致している!)
次に より
二次関数への応用:グラフとの関係
二次関数への応用:グラフとの関係
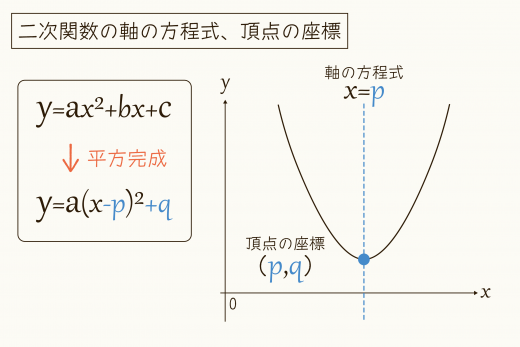
二次関数 を平方完成すると,軸の方程式や頂点の座標が一目でわかるようになります。
二次関数 について,
- 軸の方程式:
- 頂点の座標:
である。
発展
発展
平方完成の発展形を2つ紹介します。
1:立方完成(立体完成)
平方完成と同様な考え方で三次式の二次の項を消すことを立方完成(または立体完成)と言います。
と変形します。
を立方完成せよ。
まず二次の係数を見て を決める。
次に一次の項と定数項を調節すると を得る:
応用例:立方完成は三次方程式の解法に用いられます。→カルダノの公式と例題【三次方程式の解の公式】
2:四次式を平方完成する
なる四次式を以下のように変形する操作も用いられます。
を上の形に変形せよ。
と変形できるとする。
まず,三次の項を比較して より
さらに二次の項を比較して より
あとは も調節すると,
を得る。
ー応用例ー
-
四次関数の二重接線を求めるときに使います。→四次関数の二重接線を素早く求める方法
-
整数問題でもときどき登場します。→整数問題のテクニック:平方数でないことの証明の例2(この例は の項がないのであまり面白くない)
ところで,なんで平方完成って言うのでしょうか,平方変形とかでいいような気もします。










