四次関数の二重接線を素早く求める方法
二重接線とは,とある曲線に相異なる2つの点で接するような直線のことです。複接線と呼ばれることもあります。
多くの四次関数には二重接線が存在する。二重接線は平方完成を用いて簡単に求めることができる。
例題
例題
この記事では,以下の例題を使って「普通の解法」と「平方完成を用いてすばやく求める解法」を解説します。
四次関数 の二重接線の方程式を求めよ。
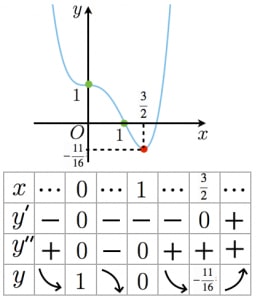
解答の前に,この四次関数のグラフの概形を書いておきます。細かいグラフの書き方は四次関数のグラフの概形と例題2問を参照して下さい。
図のグラフの形から,傾きが負の二重接線が一本引けそうだと分かります。
小技の威力に感動していただくためにも,ぜひこの問題を自力で解いてみてください,けっこう時間がかかってしまう人が多いと思います。
普通の解法
普通の解法
四次関数の二重接線を求める方法はいくつもあります。その中でも,重解を用いる有名で比較的楽な方法を解説します。
以下の定理を前提知識として使います。
多項式で表される曲線 と が で接する
が を重解に持つ。
考え方は難しくありませんが計算に工夫が必要です。
与えられた四次関数と が で接するとき, となる。あとはこれを展開して係数比較して を求めればよい。
上式の右辺は
となる。まず, と の係数を比較すると,
以上二つの式より となる(ここで と を求めにいく必要はない)。

次に, の項と定数項を比較すると,
以上より,求める二重接線の方程式は
グラフと照らしあわせても納得の答えですね。計算をわりと工夫しましたが,それでもこれくらいの計算量にはなってしまいます。
平方完成を用いてすばやく求める解法
平方完成を用いてすばやく求める解法
実は,平方完成を用いるともっと楽に計算できます!
与えられた四次関数と が で接するとき,
つまり,
よって, を(二次式の二乗+1次関数)となるように変形する(→平方完成のやり方といくつかの発展形の例題6)と, となる(→注)。
よって求める二重接線の方程式は
注:厳密には,以下の2つを述べる必要があります。
- 他に二重接線が無いこと(上記以外に(二次式の二乗+1次関数)と変形する方法が無いこと)
- の判別式は正であり相異なる実数解を二つもつこと
最短で得点力を上げる!高校数学の問題集〈典型250問〉の問題61では,接線の方程式を係数比較する力技も紹介しています。
実はこの小技,昨日友人に教えてもらいました。けっこう感動しました!











