点と平面の距離公式と例題・2通りの証明
座標平面上で という式は平面を表す。この平面と点 の距離は,

点と平面の距離公式について,意味・例題・証明を整理しました。大学入試でもたまに役立つ公式です。
点と平面の距離公式の例題
点と平面の距離公式の例題
点と平面の距離公式: を使って問題を解いてみます。
点 と平面 の距離を求めよ。
公式 に代入するだけ。 であり,平面の方程式から なので,距離は

補足:
- 分子の絶対値,分母のルートを忘れやすいので注意しましょう。
- 座標空間において,平面が という1次式で表されることは,平面の方程式とその3通りの求め方で解説しています。
- 「平面と点 の距離」とは, から平面におろした垂線の長さのことです。
点と直線の距離公式の3次元バージョン
点と直線の距離公式の3次元バージョン
「点と平面の距離公式」は,2次元の場合の「点と直線の距離公式」 と合わせて覚えておくと良いです。
- (2次元平面における)点と直線の距離公式:
点 と直線 の距離は - (3次元空間における)点と平面の距離公式:
点 と平面 の距離は
2つの公式は非常に似ていますね。証明も似ています。点と直線の距離公式については点と直線の距離公式:例題と5通りの証明で解説しています。
点と平面の距離公式の証明
点と平面の距離公式の証明
2通りの証明を紹介します。
空間ベクトルを使った証明
点 から平面 に下ろした垂線の足を とします。
前提知識として,ベクトル が平面 と垂直なベクトル(法線ベクトル)であることを使います。→平面の方程式とその3通りの求め方
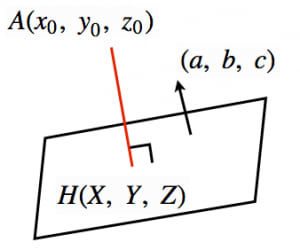
点から平面におろした垂線の足 の座標を とおく。 は の法線ベクトルと平行なので実数 を用いて, と表せる。あとは, が 上にある条件: を用いて を求めればよい。
に注意して,紫の式の両辺に対して との内積を取ると,
となる。
なので,
よって, の長さ,すなわち の長さは,
となり点と平面の距離公式が導出できた。
ヘロンの公式を使った証明
四面体の体積を二通りの方法で表します。
ヘロンの公式を応用する部分以外は二次元の場合(点と直線の距離公式の証明)と全く同じです。計算はやや大変で省略している部分もあるので,難しければ二次元の場合で確認してみてください。
のとき,点と直線の距離公式より成立。 のときも同様。以下 が全て でない場合を考える。
点 を通り 軸, 軸, 軸に平行な直線と平面 の交点をそれぞれ とおく。
とおく である。
求めたい距離を とおくと,四面体 の体積を二通りの方法で表すことにより,
ただし, は三角形 の面積。
次に, を で表す。
ヘロンの公式の変形版(ヘロンの公式の下部参照)より,三辺の長さが である三角形の面積 は
を満たすので,これに の式を代入して整理すると,
となる。
よって,
平面の方程式を利用して の座標を求めることにより,
となるので,これらを上式に代入して整理すると
が得られ証明完了。
二次元の場合の証明をそのまま三次元に拡張できる場合もあれば,拡張の際に工夫が必要となる場合もあります。











