四次関数のグラフの概形と例題2問
四次関数のグラフの特徴,書き方について解説します。四次関数は,教科書では数学2の発展事項として扱われています。
四次関数のグラフの概形
四次関数のグラフの概形
まずは四次関数のグラフの概形について,おおまかな特徴を解説します。
以下,四次の係数 が正であるような四次関数について考えます。
四次関数 のグラフの概形
特徴1.上から入ってきて上に抜けていく
特徴2.極小点(コブ)は一つか二つ

特徴1について, の絶対値が十分大きいとき, の項が支配的となります。したがって,グラフは上から入ってきて上に抜けていく形(さらに,端の方では下に凸)となります。
特徴2について, は三次方程式となり,解は高々三つです。したがって,極値を取る点も高々三つです。よって,極小点は二つ以下となります。
以下,極小点が二つの場合と一つの場合の例題を見ていきます。
例題1
例題1
極小点が二つのパターンです。三次方程式 が異なる実数解を三つ持つときは極大点,極小点を滑らかにつなげることで概形が書けます。
四次関数 のグラフの概形を書け。なお,変曲点を求める必要はない。
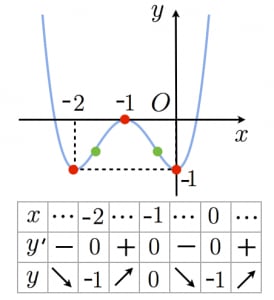
よって, は で符号変化が起こる。
に注意すると,増減表,グラフの概形は図のようになる。
なお図より,変曲点の大雑把な位置も分かる。 を解くことで変曲点の座標を正確に求めることもできる。
注:「グラフの概形」と言われたときに増減だけでよいのか,凹凸も調べるべきなのかは 問題の指示or概形を書くことで何をしたいのかによります。
注2:例題1の関数は と変形できるので,グラフは に関して対称となります。
例題2
例題2
極小点が一つのパターンです。三次方程式 の異なる実数解が二つ以下しかない場合です。
四次関数 のグラフの概形を書け。なお,凹凸も調べよ。

よって, で となるが, は重解なので符号変化は起きず,極値ではない。 で極小値 を取る。
次に,二階微分を求める よって, と で の符号変化が起きるので変曲点となる。
以上に注意すると,グラフの概形,増減表は図のようになる。
まとめ
まとめ
-
四次関数のグラフの概形は大きく分けて2タイプ,コブが一つか二つ(ただし,変曲点の位置を考えるともう少し細かくタイプが分かれる)。
-
導関数,二階導関数の符号変化を見て増減表とグラフの概形を書けるように。
増減表とグラフの概形の図を作るのにかなり苦労しました。











