箱ひげ図の見方・読み取り方(中央値,平均値,四分位数,最大・最小値)
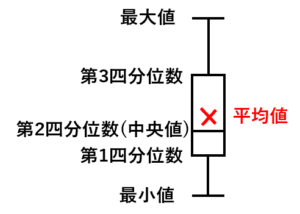
箱ひげ図とは,図のように「最大値・最小値・四分位数」の情報を表現したグラフです。箱ひげ図には平均値の情報が含まれることもあります。
箱ひげ図を見れば,データの分布をおおまかに把握できます。
箱ひげ図の見方・読み取り方
箱ひげ図の見方・読み取り方
箱ひげ図では,長方形(はこ)と線(ひげ)を使って「最大値・最小値・四分位数」の情報を表現します。

四分位数(第1四分位数,中央値,第3四分位数)
真ん中の長方形(はこ)は,四分位数を表します。つまり,
- 箱の下側が,第1四分位数(下から1/4の部分にあるデータの値)
- 箱の真ん中の横線が,第2四分位数(中央値,ちょうど真ん中にあるデータの値)
- 箱の上側が,第3四分位数(上から1/4の部分にあるデータの値)
を表します。
最大値,最小値
また,上下のひげは,最大値と最小値の情報を表します。
つまり,ひげの長さがデータの範囲を意味します。
平均値
さらに,平均値をバツ印で表現することもあります。この平均値の印の記法は統一されているわけではありません。三角など他の記号を用いて表されることもしばしばあります。
箱ひげ図を使った例題
箱ひげ図を使った例題
とある学校のA組,B組の生徒の身長のデータについて以下のような箱ひげ図を作成した。A組の生徒数は40人,B組の生徒数は30人である。この箱ひげ図から読み取った記述として正しいものを選べ。

- データの範囲はB組よりA組の方が広い。
- B組の生徒で,160cm以上の生徒は5人より少ない。
- ◯:最小値は同じくらいで,最大値がA組の方が明らかに大きいので,データの範囲はA組の方が広い。
- ×:B組の第3四分位数は160cmより低いが,160cmより大きい生徒が5人以上いる可能性もあるので,正しくない。
箱ひげ図のメリット
箱ひげ図のメリット
箱ひげ図を使うと,データの情報を簡潔に表現できます。
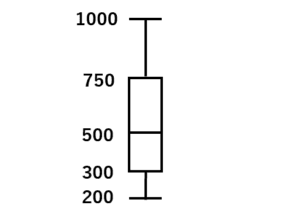
例えば「ある地域の年収は,最大1000万,最小200万,第1四分位数は300万,中央値は500万,第3四分位数は750万」のように文章で表現するよりも,箱ひげ図を使った方が分かりやすいです。
箱の部分を見ることで「真ん中半分の人は300万から750万」ということもすぐに分かります。
箱ひげ図に関する注意
箱ひげ図に関する注意

- 箱ひげ図は,図のように横向きに書くこともあります。
- 上記で説明したのは高校数学の教科書に載っている「外れ値を考慮しないバージョン」です。外れ値を考慮した箱ひげ図(こちらの方が一般的だと思います)については後述します。
- 箱ひげ図には,バツ印(平均値)を書かないこともあります。
- 第1四分位数とはデータの中で小さい方から ,第3四分位数とはデータの中で大きい方から にある数です。四分位数の求め方にはいくつか流儀があるので注意が必要です。→四分位数の求め方といろいろな例題
外れ値を考慮した箱ひげ図
外れ値を考慮した箱ひげ図

中央値,四分位数は外れ値に引っ張られませんが,最大値,最小値は外れ値に引っ張られます。つまり,教科書の箱ひげ図の定義の場合「箱」は外れ値に引っ張られませんが「ひげ」は外れ値に引っ張られます。
そこで「外れ値を考慮する立場」では,上下のひげはともに箱の1.5倍以下の長さとして,もしそれを越えるようなデータがある場合は外れ値とみなす(最大・最小値とはみなさない,ひげはそこまで伸ばさない)ことにします。
ちなみに,はこ・ひげの他に,最大値・最小値の外側にいくつか点が表示されることがあります(Excel等を使って箱ひげ図を作ったことがある方は,みたことがあるかもしれません)。これは外れ値を表現したものです。
都合の悪い実験データを外れ値として意図的に隠すのはいけませんよ!











