円に内接する四角形の性質とその証明まとめ

更新日時 2022/01/16

円に内接する四角形の性質を整理しました。 円に内接する四角形 円周角の定理からトレミーの定理まで，全部使えるようになっておきましょう！

目次

円周角の定理

円に内接する四角形を見たら，まずは円周角の定理が使えないか考えてみるとよいです。

性質0

円周角の定理が使える。つまり，円に内接する四角形 ABCDABCD において，

∠DAC=∠DBC\angle DAC=\angle DBC などが成り立つ。

円に内接する四角形と円周角

以下の性質の多くは円周角の定理に基づいています。

向かい合う角の和は180°

次は，円に内接する四角形における一番有名な性質です。

性質1

向かい合う内角の和は 180∘180^{\circ} である。つまり，

∠A+∠C=180∘\angle A+\angle C=180^{\circ}

∠B+∠D=180∘\angle B+\angle D=180^{\circ}

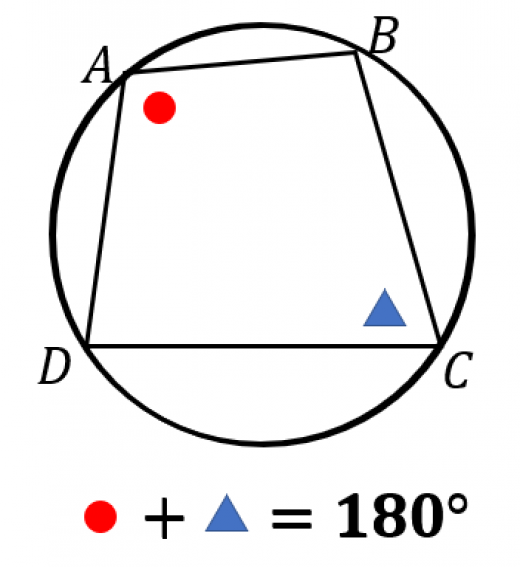
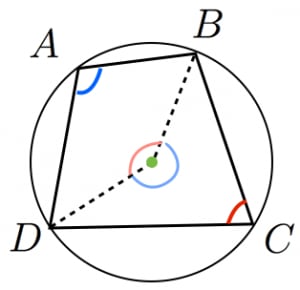
円に内接する四角形の対角の和

証明

円に内接する四角形の対角の和

円周角と中心角の関係より

∠A+∠C\angle A+\angle C
＝青＋赤
＝12\dfrac{1}{2} (薄い青＋薄い赤) =12×360∘=180∘=\dfrac{1}{2}\times 360^{\circ}=180^{\circ}

性質1の逆も成立します。つまり，向かい合う内角の和が 180∘180^{\circ} である四角形は円に内接します。

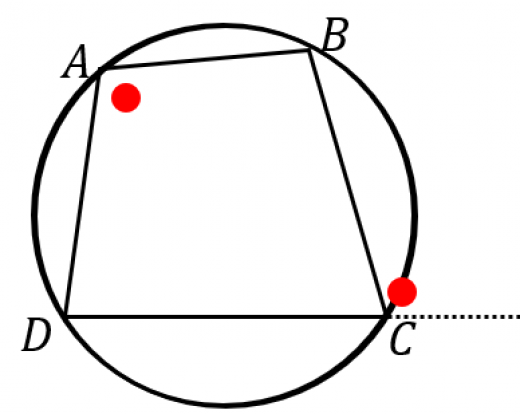
また，性質1は「外角」を使って表現されることも多いです。

性質1’

∠A=「∠C\angle A=「\angle C の外角」

などが成立する。

円に内接する四角形と外角

円に内接する四角形の面積

次に，円に内接する四角形の面積の性質です。

性質2（ブラーマグプタの公式）

AB=a,BC=b,CD=c,DA=d,s=a+b+c+d2AB=a,BC=b,CD=c,DA=d,s=\dfrac{a+b+c+d}{2} とおくと，四角形 ABCDABCD の面積は，

S=(s−a)(s−b)(s−c)(s−d)S=\sqrt{(s-a)(s-b)(s-c)(s-d)}

円に内接する四角形の面積

入試でもけっこう使えます。ブラーマグプタの公式とその証明に二通りの証明を記載しています。

また，円に内接する四角形を2つに割った三角形の面積比について，以下の性質が成立します。

性質3

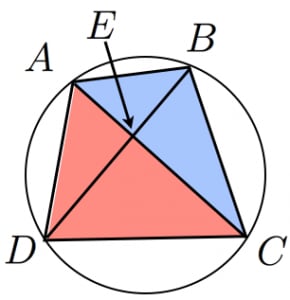
内接四角形と面積

AD×DC:AB×BC=∣ADC∣:∣ABC∣=DE:EBAD\times DC: AB\times BC\\=|ADC|:|ABC|\\=DE:EB

ただし，対角線の交点を EE とおき，三角形 ABCABC の面積を ∣ABC∣|ABC| などと書きました。

証明
  • ∣ADC∣=12AD×DCsin⁡D|ADC|=\frac{1}{2}AD\times DC\sin D と ∣ABC∣=12AB×BCsin⁡B|ABC|=\frac{1}{2}AB\times BC\sin B
  • 性質1より sin⁡B=sin⁡D\sin B=\sin D

の二点から1つめの等号が成立。

2つめの等号は「底辺が共通な三角形の面積比は高さの比に等しい」ので成立。

方べきの定理

「円に内接する四角形の性質」ではありませんが，円周上に4点がある場合方べきの定理を使うことが多いです。

性質4(方べきの定理)

AE×EC=BE×EDAE\times EC=BE\times ED

また，ADAD と BCBC の交点を FF とおくと

FA×FD=FB×FCFA\times FD=FB\times FC

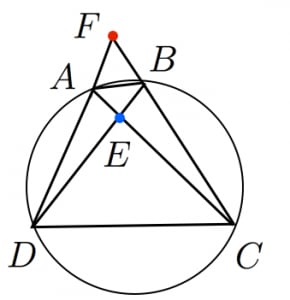
円に内接する四角形と方べき

大学入試共通テストをはじめ，入試で頻出です。性質0，1と比べて少し気づきにくいので注意が必要です。

方べきの定理の証明は方べきの定理の意味と2通りの証明を参照して下さい。

注：方べきの定理の逆も成り立ちます。四角形が円に内接することの証明に方べきの定理の逆を使うことはけっこう多いです。

トレミーの定理

性質5（トレミーの定理）

AB×CD+AD×BC=AC×BDAB\times CD+AD\times BC=AC\times BD

トレミーの定理

入試問題の検算や，数学オリンピックの証明問題などにときどき使えます。

証明や応用例はトレミーの定理とその証明，応用例を参照して下さい。

注：トレミーの定理の逆も成り立ちます。ただ，四角形が円に内接することの証明にトレミーの定理の逆を使うことはほとんどありません。

トレミーの定理がもっと有名になると嬉しいです。

Tag:数学Aの教科書に載っている公式の解説一覧

この記事の編集者
マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！

関連記事
人気記事