トレミーの定理の証明を3通り紹介します。
1. 三角形の相似を使った証明
方針
補助線を1本引くと,相似な三角形が2組現れます。発想力が必要ですが美しい証明です。
証明
対角線 BD 上に,∠DAM=∠BAC となるように点 M を取る。
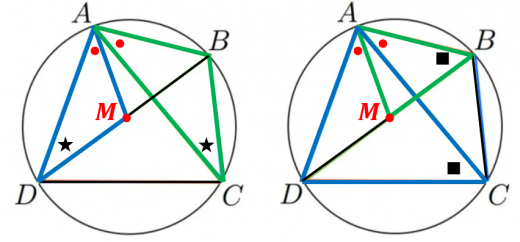
すると,左図で円周角の定理より★の角度は等しいので三角形 AMD と ABC は相似。よって,
AD:AC=DM:BCAD×BC=AC×DM
同様に,右図で円周角の定理より■の角度は等しいので三角形 ADC と AMB が相似。よって,
AB:AC=BM:CDAB×CD=AC×BM
以上2つの式を足すと,トレミーの定理を得る:
AB×CD+AD×BC=AC×(BM+DM)=AC×BD
2. 余弦定理で対角線の長さを計算する証明
方針
余弦定理を用いて,対角線の長さを四角形の4辺の長さで表します。機械的な計算で証明できます。
証明

AB=a,BC=b,CD=c,DA=d,AC=e,BD=f
とおく。また,∠ABC=θ とおく(すると,円に内接する四角形の性質より ∠ADC=π−θ となる)。
三角形 ABC に余弦定理を使うと,
2aba2+b2−e2=cosθ
三角形 ADC に余弦定理を使うと,
2cdc2+d2−e2=cos(π−θ)
ここで,cosθ=−cos(π−θ) より
2aba2+b2−e2=−2cdc2+d2−e2
この等式を e2 について解くと,
e2=ab+cd(ac+bd)(ad+bc)
全く同様にして
f2=ad+bc(ac+bd)(ab+cd)
もわかる。以上2式を辺々掛け合わせて平方根を取ると,
ef=ac+bd
となり,トレミーの定理を得る。
3. 正弦定理による証明
方針
正弦定理を用いて両辺を角度の情報に変換します。機械的な計算で証明できます。
証明

円の半径を R とする。図のように
θ1,⋯,θ4
を定める。正弦定理より,
ac+bd=(2Rsinθ1)(2Rsinθ3)+(2Rsinθ2)(2Rsinθ4)
同様に,
ef=4R2sin(θ1+θ2)sin(θ2+θ3)
よって,トレミーの定理 ac+bd=ef を証明するには,
sinθ1sinθ3+sinθ2sinθ4=sin(θ1+θ2)sin(θ2+θ3)
を示せばよい。θ4=180∘−(θ1+θ2+θ3) に注意すると,
sinθ1sinθ3+sinθ2sin(θ1+θ2+θ3)=sin(θ1+θ2)sin(θ2+θ3)
を示せばよい。両辺を頑張って加法定理で展開すると一致することがわかる。
具体的には,両辺ともに以下の式になる:
sinθ1sinθ2cosθ2cosθ3+cosθ1sin2θ2cosθ3+sinθ1cos2θ2sinθ3+cosθ1sinθ2cosθ2sinθ3

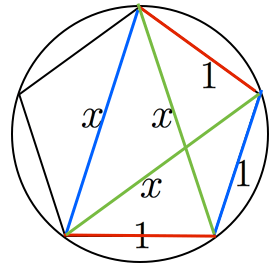




 正七角形は円に内接する。よって,トレミーの定理より がわかる。両辺を で割ると正七角形調和が証明された。
正七角形は円に内接する。よって,トレミーの定理より がわかる。両辺を で割ると正七角形調和が証明された。










