スチュワートの定理の証明とその仲間

スチュワートの定理は覚える必要はありませんが，導出できるようになっておきましょう。

スチュワートの定理は覚えなくてよいです。なぜなら「証明が難しくない」かつ「覚えにくい」からです。

その代わり，以下の事実を覚えておくとよいでしょう。

• 三角形とその辺の内分点があれば，線分の長さの関係式を余弦定理で導ける。
• 形状の分かっている三角形と辺の内分点 $P$ に対して，$AP,BP,CP$ のうち1つ分かればスチュワートの定理と $BP+CP=a$ を用いて残りの2つも求められる。

実際にスチュワートの定理が必要になったら，そのつど余弦定理を用いて導けばよいです。ちなみに，スチュワートの定理の応用例としては三角形における距離の二乗の和の公式の図形による証明などがあります。

スチュワートの定理は非常に一般的な形をしています。以下の2つの特殊形を使う機会が多いです。

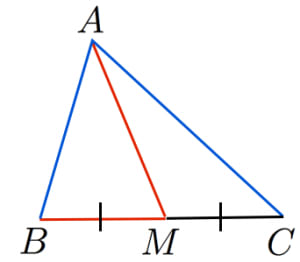
スチュワートの定理は，$P$ が $BC$ の中点 $M$ のときはパップスの中線定理と一致します。実際，スチュワートの定理において $BP=CP=\dfrac{a}{2}$ とすれば中線定理が導けます。つまり「中線定理はスチュワートの定理の特殊形」です。→中線定理の3通りの証明

$\angle BAP=\angle CAP$ のときは，「辺の比に関する角の二等分線定理」より $BP=\dfrac{ac}{b+c},\:CP=\dfrac{ab}{b+c}$ となります。これを，スチュワートの定理の左辺に代入して整理することで，上記の公式が得られます。上記の公式も，スチュワートの定理の特殊形です。 →角の二等分線に関する重要な3つの公式

スチュワートの定理は直接役に立つことは少ないですが，中線定理や角の二等分線の公式を統一的に扱うことができ，知っていると視野が広がります。