全ての三角形が二等辺三角形であることの証明!?
更新
有名な嘘の証明です。
「全ての三角形は二等辺三角形,さらに正三角形である」 を証明します。
もちろんそのような命題が成立するはずはないので,証明のどこかに嘘があります。探してみてください!
全ての三角形が二等辺三角形であることの証明
全ての三角形が二等辺三角形であることの証明
「全ての三角形が二等辺三角形である,さらに正三角形である」ことの巧妙な証明です。
-
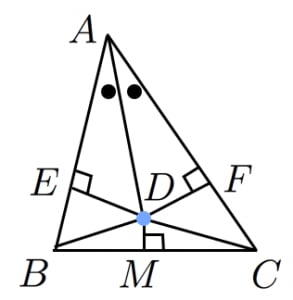
三角形 において,角 の二等分線と の垂直二等分線の交点を とおく。 から に下ろした垂線の足を とおく。
-
このとき,直角三角形 と は合同(角度が全て等しく斜辺は共通)。よって , 。
-
また, の中点を とおくと三角形 と は合同(二辺とその間の角がそれぞれ等しい)。よって
-
上の二つの結果より,三角形 と は合同(直角三角形において斜辺と他の一辺がそれぞれ等しい)。よって
-
以上により
-
よって,三角形 は二等辺三角形である。同じことが辺 に対しても言えるので,結局三角形 は正三角形である。
さあ,どこに嘘があるでしょうか? ここから下に答えがあります,答えを見る前に考えてみてください!
出題意図
(スクロールの勢い余って答えを見てしまうのを防ぐために)嘘の証明を学ぶ意味について考えてみます。
- 単純にクイズとしておもしろい,友達に出題したくなる。
- それっぽい証明の穴をつくのは数学の研究でも重要。
- 嘘の証明から学ぶこともある。この場合は図形問題の練習になる。
答え
答え
意外な所に落とし穴があります!

が三角形 の内部にはないので上の図が間違っている。よって,5において 成立しないので証明は間違い。
というのが答えです。例えば のとき,角 の二等分線と の交点を とおくと,角の二等分線定理より となり, 線分 は の垂直二等分線と交わりません。
正三角形であることの証明(修正版)
正三角形であることの証明(修正版)
上の「答え」に対して,嘘の証明を修正してみました!

が三角形 の外部にあるときも,さきほどの証明において1〜4は成立する。
5は と修正することで結局 が証明できる。よって,三角形 は二等辺三角形であり,したがって(対称性より)正三角形である。
この証明の反論も考えてみてください!下に答えがあります。
修正版の証明のまちがい

やっぱり図が間違いです。正しい図を書いてみると,例えば のとき, は線分 上になく,一方 は線分 上にあります。したがって, になります。よって,やはり5の部分が間違い。
ちなみに,このような図になるのは以下のいずれかの方法で納得できます。
- が よりも極端に短いような三角形を考えて丁寧に図を書いてみる。
- シムソンの定理→シムソンの定理とその2通りの証明
最終的にシムソンの定理で説明できることに感動。
Tag:難しめの数学雑学・ネタまとめ











