四角形の重心の2通りの求め方と注意点
更新
三角形の重心は高校数学で習いますが,四角形については習いません。というわけで,四角形の重心について考えます。
四角形の物理的重心
四角形の物理的重心
(密度に偏りのない)四角形の板について考えます。「 を支えるとその四角形全体を支えることができる」ような点 を物理的重心と呼ぶことにします(※)。
物理的重心の求め方を2通り紹介します。以下, は三角形 の重心を表します。 は三角形 の面積を表します。他も同様です。
1:線分 を に内分する点が物理的重心。
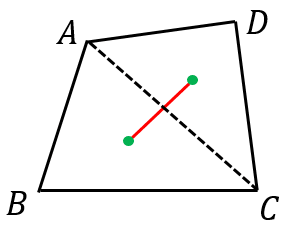
四角形の重心は 対角線で分けた2つの三角形の重心を結ぶ線分上にあるというわけです。なぜ1が成立するかについては,モーメントのつりあいを考えれば分かります(面積分が登場するのでここでは割愛します)。考えてみてください!
そして,1を認めれば以下の2も物理的重心であることが分かります。
2:線分 と線分 の交点が物理的重心。
※このページでは,中身がスカスカで質点だけに同じ重さがかかっている状況ではなく, 中身が詰まっている剛体を支える点を「物理的重心」と呼びます。
中点と中点の中点
中点と中点の中点
もう一つ 四角形の重心っぽい点 を考えてみます。具体的には,
-
の中点と の中点を結ぶ線分の中点
-
の中点と の中点を結ぶ線分の中点
-
4頂点の座標の平均
は全て一致する(座標計算 or ベクトル計算により分かる)ので,この点を としてみます。ベクトルで書くと, という感じです。
と は一致しない
と は一致しない
残念ながら, 物理的重心 と重心っぽい点 は一致しません。

これは,図のような「二等辺三角形に近い四角形」を考えれば分かります。
実際, は中点と中点の中点なので, の中点あたりに来ますが,物理的な重心 は三角形の重心(→補足)の性質から を に内分する点あたりに来ます。
補足:三角形では「物理的な重心」と「座標の平均の点」が一致します(これも厳密にはモーメントのつりあい→積分計算で示す必要がある)。
関連記事:四面体の重心の存在証明と応用例
幼いころクイズ番組で四角形の重心についての問題を見た記憶があります。











