RSA暗号の仕組みと安全性・具体例

更新 2022/01/29

RSA暗号とは，公開鍵暗号方式の具体的なアルゴリズムです。RSA暗号の仕組みと安全性について解説します。

RSA暗号の仕組み

前提知識（公開鍵・共通鍵暗号，整数の性質）

以下の2つの知識があると読みやすいです。

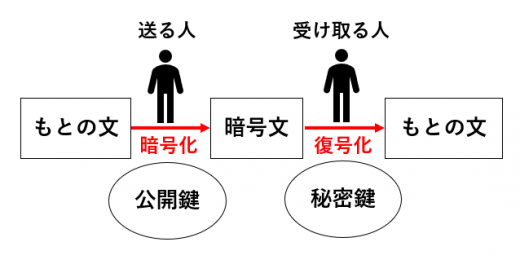
公開鍵暗号方式についてなんとなくでも知っていると読みやすいです。→共通鍵暗号と公開鍵暗号の仕組み
「 $a$ と $b$ を $n$ で割った余りが等しい」とき， $a\equiv b\pmod{n}$ と書きます。→合同式の基礎

RSA暗号の仕組み・アルゴリズム

1．メッセージを受け取る側の準備
大きな素数 p,qp,qp,q を生成し，n=pqn=pqn=pq とする
(p−1)(q−1)(p-1)(q-1)(p−1)(q−1) と互いに素な整数 k1k_1k1​ を取ってくる
k1k2≡1(mod(p−1)(q−1))k_1k_2\equiv 1\pmod{(p-1)(q-1)}k1​k2​≡1(mod(p−1)(q−1)) なる k2k_2k2​ を取ってくる（→補足1）
nnn
と
k1k_1k1​
を公開する（公開鍵），k2k_2k2​
は公開しない（秘密鍵）
2．メッセージを送る側の暗号化方法
送りたいメッセージを mmm とする。ただし，mmm は nnn 未満の正の整数とする
公開鍵を用いてmk1m^{k_1}mk1​ を nnn で割った余りを計算し，これを暗号文（CCC とおく）とする
3．メッセージを受け取る側の復号方法
暗号文
CCC
と秘密鍵
k2k_2k2​
を用いてCk2C^{k_2}Ck2​ を nnn で割った余りを計算すると，実はこれがもとのメッセージに一致する（→補足2）！
4．安全性
暗号文
CCC
と公開鍵
n,k1n,k_1n,k1​
が分かっても（現実的な時間では）mmm
を復元することはできない（と信じられている）

補足1：公開鍵・秘密鍵の準備について

以下の「有名な定理」により $0\leq k_2\leq (p-1)(q-1)$ のもとで $k_2$ は一意に定まります。

有名な定理

$a$ と $b$ が互いに素なとき $ax\equiv 1\pmod{b}$ なる $x$ が $1\leq x\leq b-1$ の間ではただ一つ存在する。

証明は，例えば背理法の意味といろいろな例とよくある間違いの例題2から分かります。

また， $k_1,k_2$ の計算は高速にできることが知られています。

補足2：復号化がうまくいく理由

暗号化： $m^{k_1}\bmod{n}$
復号化： $C^{k_2}\bmod{n}$

でうまく復号できていることを証明します。証明にはフェルマーの小定理を使います。数学がまあまあ得意な高校生なら理解できるレベルの内容です。

証明

$m^{k_1k_2}\equiv m\pmod{n}$ を証明すればよい。

$n=pq$ なので， $m^{k_1k_2}\equiv m\pmod{p}$ を証明すれば十分（対称性より $\mathrm{mod}\:q$ も同様）。

$m$ が $p$ の倍数のときは両辺ともに $p$ の倍数よりOK。

$m$ が $p$ の倍数でないとき， $k_1k_2-1$ が $(p-1)$ の倍数となるように設定したので，整数 $N$ を用いて $k_1k_2=1+(p-1)N$ とおける。よって，

$m^{k_1k_2}=m\cdot (m^{p-1})^N\equiv m\cdot 1^N=m$

ただし，途中の $\equiv$ は $\mathrm{mod}\:p$ であり，フェルマーの小定理を用いた。

RSA暗号の安全性と素因数分解

素因数分解が簡単に（短時間で）計算できればRSA暗号は破られます。

説明

暗号文 $C$ ，公開鍵 $k_1,n$ は誰でも見ることができる。

ここで $n$ を素因数分解することで $p,q$ が求まる。すると「メッセージを受け取る側の準備」と同じ方法で秘密鍵 $k_2$ が求まり，もとのメッセージ $M$ を復号できる。

幸い，大きな数の素因数分解の計算は難しいです。→素因数分解の難しさと素数判定

RSA暗号の計算例

実際にRSA暗号の計算例を見ることで，理解を深めましょう。
公開鍵・秘密鍵の準備素数として p=23,q=31p = 23, q = 31p=23,q=31 とします。n=pq=713n = pq = 713n=pq=713 です。これくらいの数であれば素因数分解は簡単ですが，あくまで計算例ということで。
(23−1)(31−1)=22×30=660(23-1)(31-1) = 22 \times 30 = 660(23−1)(31−1)=22×30=660 と互いに素な数として，k1=7k_1 = 7k1​=7 を選ぶことにしましょう。
有名な定理により，7×k2≡1mod  6607 \times k_2 \equiv 1 \mod 6607×k2​≡1mod660 の解 k2k_2k2​ は k2=283k_2 = 283k2​=283 と一意に定まります。
公開鍵として n=713,k1=7n = 713, k_1 = 7n=713,k1​=7 を公開し，秘密鍵として k2=283k_2 = 283k2​=283 を秘密にしておきます。
暗号化の処理メッセージを送る側は，478478478 という数を送りたくなったとします。n=713n = 713n=713 を法として，
4787≡673478^{7} \equiv 6734787≡673 です。C=673C = 673C=673 として，これを送ります。
復号化の処理n=713n = 713n=713 を法として，
673283≡478673^{283} \equiv 478673283≡478 です。これで，無事に解読できました！
厳密には（ppp
 などに）もっといろいろ条件があります。興味を持った方は暗号の本を読んでみてください！

この記事の監修者

マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。記事の誤植やわかりにくい等のご指摘はお気軽にメールください！