球欠,球台の体積と球冠,球帯の表面積
更新
球を平面で切り取った立体の体積,および側面の面積の求め方を解説します。結果を覚える必要はありませんが,導出方法はマスターしておきましょう。
球を切って得られる立体の名前
球を切って得られる立体の名前
球欠(spherical segment):球を一つの平面で切った立体
球冠(球帽,spherical cap):球欠の側面部分
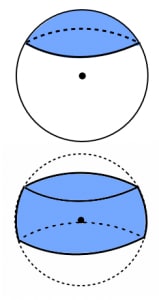
球台(spherical segment):球を二つの平行な平面で切った立体
球帯(spherical zone):球台の側面部分
球欠と球台は立体,球冠と球帯は曲面です。球欠は球の一部が欠けたもので,球帽は帽子っぽい,球台は台っぽい,球帯は帯っぽいですね(名前を覚える必要はありません)。
球欠,球台の体積
球欠,球台の体積
底面の半径が ,天面の半径が ,高さが である球台の体積は,
もとの球の半径を とおくと図より,
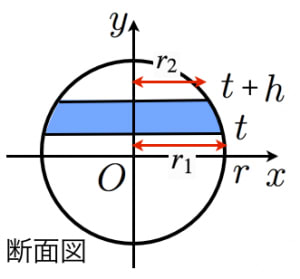
あとは を消去して で表せばよい。
まず, (*)を用いて を消す:
さらに,(*)と から となり,これを代入すると,
を得る。
なお, または とすることで球欠の体積公式: が得られます。
球冠,球帯の表面積
球冠,球帯の表面積
高校数学の範囲外ですが,計算は体積より簡単です。非常に美しい結果です。
球冠,球帯の表面積はその高さに比例する。
注:球帯の高さとは底面と天面の距離です。
球の体積と表面積の公式の覚え方・積分での求め方の表面積の証明1とほぼ同じことをやるだけです。

もとの球の半径を とする。
を十分 に近い正の数として,緯度が から の部分(帯のような図形)の表面積を考える。
周の長さは ,帯の幅は なので帯の表面積は,
よって,球帯の表面積は
(ただし, は球帯の底面の緯度, は球帯の天面の緯度)
ここで, と置換すると, より,
(ただし, は球帯の底面の「高さ」, は球帯の天面の「高さ」, は球帯の幅)
なお,球帯で とすれば球冠になります。
図を描くのが大変でした。











