2. 高校数学の美しい物語
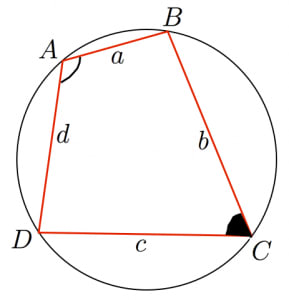
  3. ブラーマグプタの公式とその２通りの証明

ブラーマグプタの公式とその２通りの証明

更新日時 2021/03/07

ブラーマグプタの公式：

円に内接する四角形 ABCDABCD において AB=a,BC=b,CD=c,DA=dAB=a, BC=b, CD=c, DA=d とおくと，四角形 ABCDABCD の面積は，

S=(s−a)(s−b)(s−c)(s−d)S=\sqrt{(s-a)(s-b)(s-c)(s-d)}

ただし， s=a+b+c+d2s=\dfrac{a+b+c+d}{2} とおいた。

円に内接する四角形の面積を瞬時に求める公式です。

ヘロンの公式と同様，まず ss を求めてから面積 SS を計算します。

ちなみに，d→0d\rightarrow0 の極限を取ればブラーマグプタの公式はヘロンの公式と一致するので，ブラーマグプタの公式はヘロンの公式を含んでいます。

この記事ではブラーマグプタの公式の証明を2つ紹介します。1つ目は三角関数を用いた素直な方法，2つ目はヘロンの公式を用いた方法です。

目次

  • 三角関数（余弦定理）を用いたブラーマグプタの定理の証明

  • ヘロンの公式を用いたブラーマグプタの定理の証明

  • 余談

三角関数（余弦定理）を用いたブラーマグプタの定理の証明

方針：求める面積は三角形 ABDABD と CBDCBD の面積の和です。そこで，∠A\angle A を4辺の長さで表せばよいので余弦定理を用います。その後は気合いで因数分解します。

ブラーマグプタの公式

証明

S2=(12adsin⁡A+12bcsin⁡C)2=14(ad+bc)2(1−cos⁡2A)⋯(∗)=116{4(ad+bc)2−(a2+d2−b2−c2)2}⋯(∗∗)S^2=(\dfrac{1}{2}ad\sin A+\dfrac{1}{2}bc\sin C)^2\\ =\dfrac{1}{4}(ad+bc)^2(1-\cos^2A)\cdots(*)\\ =\dfrac{1}{16}\{4(ad+bc)^2-(a^2+d^2-b^2-c^2)^2\}\cdots(**)

これで四角形の面積を辺の長さで表せたのであとは因数分解する。上式は，

116(2ad+2bc+a2+d2−b2−c2)(2ad+2bc−a2−d2+b2+c2)=(a+b+c−d)2(a+b−c+d)2(a−b+c+d)2(−a+b+c+d)2=(s−a)(s−b)(s−c)(s−d)\dfrac{1}{16}(2ad+2bc+a^2+d^2-b^2-c^2)(2ad+2bc-a^2-d^2+b^2+c^2)\\ =\dfrac{(a+b+c-d)}{2}\dfrac{(a+b-c+d)}{2}\dfrac{(a-b+c+d)}{2}\dfrac{(-a+b+c+d)}{2}\\ =(s-a)(s-b)(s-c)(s-d)

ただし，途中の変形において，

（*）: A+C=180∘A+C=180^\circ より sin⁡A=sin⁡C\sin A=\sin C であることを用いた。

（**）:余弦定理より a2+d2−2adcos⁡A=b2+c2−2bccos⁡Ca^2+d^2-2ad\cos A=b^2+c^2-2bc\cos C 及び cos⁡C=−cos⁡A\cos C=-\cos A より，cos⁡A=a2+d2−b2−c22(ad+bc)\cos A=\dfrac{a^2+d^2-b^2-c^2}{2(ad+bc)} であることを用いた。

ヘロンの公式を用いたブラーマグプタの定理の証明

方針：三角形の面積ならヘロンの公式を用いて辺の長さだけで表せます。よって，面積を求めたい四角形を「大きい三角形」ー「小さい三角形」と捉えます。すると，相似な三角形が出現してうまくいきます。

四角形 ABCDABCD が長方形の場合は簡単なので長方形でないとする。すると ADAD と BCBC が平行でないと仮定しても一般性を失わないので，交点を EE とおく。 EA=p,EB=qEA=p, EB=q とおく。

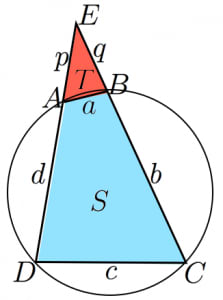
ブラーマグプタの公式の証明

△ EABEAB と△ ECDECD は相似なので，

a:c=q:p+d　→　a(p+d)=cqa:c=p:q+b　→　a(q+b)=cpa:c=q:p+d\\　→　a(p+d)=cq\\ a:c=p:q+b\\　→　a(q+b)=cp

この2式を辺々和と差を取る：

p+q=a(b+d)c−ap+q=\dfrac{a(b+d)}{c-a}

p−q=a(b−d)c+ap-q=\dfrac{a(b-d)}{c+a}

また，三角形 EABEAB の面積を TT とおくと，相似な三角形の面積比は辺の比の2乗なので，

T:T+S=a2:c2T:T+S=a^2:c^2

以上から，

S=c2−a2a2T=c2−a24a2(a+p+q)(−a+p+q)(a−p+q)(a+p−q)=c2−a24a2(a+a(b+d)c−a)(−a+a(b+d)c−a)(a−a(b−d)c+a)(a+a(b−d)c+a)=14(−a+b+c+d)(a−b+c+d)(a+b−c+d)(a+b+c−d)=(s−a)(s−b)(s−c)(s−d)S=\dfrac{c^2-a^2}{a^2}T\\ =\dfrac{c^2-a^2}{4a^2}\sqrt{(a+p+q)(-a+p+q)(a-p+q)(a+p-q)}\\ =\dfrac{c^2-a^2}{4a^2}\sqrt{(a+\dfrac{a(b+d)}{c-a})(-a+\dfrac{a(b+d)}{c-a})(a-\dfrac{a(b-d)}{c+a})(a+\dfrac{a(b-d)}{c+a})}\\ =\dfrac{1}{4}\sqrt{(-a+b+c+d)(a-b+c+d)(a+b-c+d)(a+b+c-d)}\\ =\sqrt{(s-a)(s-b)(s-c)(s-d)}

ただし，1行目から2行目の変形にヘロンの公式を用いた。

この記事の編集者
マスオ

高校数学の美しい物語の管理人。「わかりやすいこと」と「ごまかさないこと」の両立を意識している。著書に『高校数学の美しい物語』『超ディープな算数の教科書』。

人気記事
  2. 高校数学の美しい物語
  3. ブラーマグプタの公式とその２通りの証明
分野別
レベル別
他