自由落下の公式と例題

更新 2021/05/29

高校物理の基本中の基本である自由落下について，定義と公式を確認し，いくつかの例題を考えます。

自由落下の定義と公式

自由落下とは，「重力のみを受ける運動」のことです。質点の質量を mmm とすれば，Newtonの運動方程式より，鉛直方向上向きを正にとって，
ma=−mg
m a = -mg
ma=−mg
∴a=−g
\therefore a = -g
∴a=−g
となるので，自由落下は等加速度運動の一種であるということになりますね。
等加速度運動の公式に a=−ga = -ga=−g を代入して，自由落下の公式は以下のようになります。導出は等加速度運動・等加速度直線運動の公式を参考にしてください。
自由落下運動の公式(鉛直上向きが正の時)
v(t)=−gt+v0(1)
v(t) = -gt +v_{0} \tag{1}
v(t)=−gt+v0​(1)
x(t)=−12gt2+v0t+x0(2)
x(t) = -\dfrac{1}{2}g t^2 + v_{0} t + x_0 \tag{2}
x(t)=−21​gt2+v0​t+x0​(2)
v2−v02=−2g(x−x0)(3)
v^2 - v_{0}^{2} = -2g(x-x_0) \tag{3}
v2−v02​=−2g(x−x0​)(3)
自由落下運動の結果をグラフで表してみましょう。
v−tv-tv−t グラフは以下のようになります。
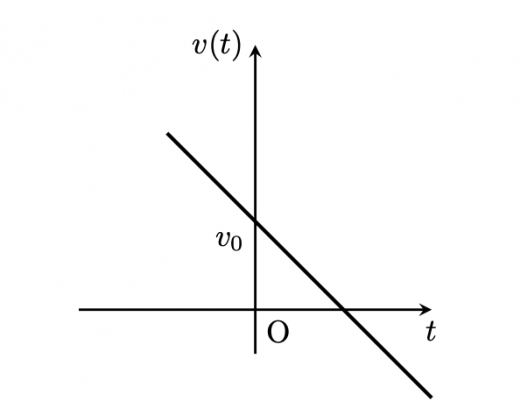
x−tx-tx−t グラフは以下のようになります。
また，直接 x−tx-tx−t グラフを書かずとも，v−tv-tv−t グラフの面積から変位を求められるということも覚えておいてください。これは xxx と vvv の間に積分の関係があることからわかります。

自由落下運動の例題

自由落下運動の例題をいくつか見てみましょう。まずはシンプルな問題から。

例題1

質量 $m$ の質点を，高さ $h$ の場所から静かに落とす。この質点が地上に到達した時の速さと時間を求めよ。空気抵抗は無視できるとする。

この問題は公式に当てはめるだけです。

解答例

問題より，初期条件は

$\begin{aligned} v_0 = 0 \\ x_0 = h \\ \end{aligned}$

として良い。

求める速さと時間をそれぞれ $v(>0)$ ，　 $t(>0)$ とする。公式(3)より，

$v^{2} - v_{0}^{2} =2 (-g) (0- h) \\ \therefore v^2 = 2gh \\ \therefore |v| = \sqrt{2gh}$

また，公式(1)より，鉛直方向上向きを正としていることに注意して，

$-\sqrt{2gh} = (-g) t + 0 = -gt$

$\therefore t =\sqrt{\dfrac{2h}{g}}$

この結果は質点の質量に依らないということが面白いですね。真空な環境であれば，羽も鉄球も同じ挙動をするということです。

続いて慣性力を考えなければならない場面を考えてみましょう。

例題2

高さ $2L(>h)$ のエレベーターの天井に，質量 $m$ のおもりが糸で吊るされている。おもりとエレベーターの床との距離をhとする。

(1)初め，エレベーターは加速度 $g$ で上昇している。この時の糸の張力 $T$ を求めよ。

途中で糸を切った。このときを $t=0$ とする。

(2)エレベーターが加速度 $g$ で上昇しているとき，おもりが床または天井に到達する時刻 $t_2$ を求めよ。

(3)エレベーターが加速度 $3g$ で下降しているとき，おもりが床または天井に到達する時刻 $t_3$ を求めよ。

(4) $t_3 >t_2$ となるような $L$ の条件を求めよ。

慣性力のことを理解していれば，本質では例題1と同じことをしていることがわかります。慣性系については，慣性の法則〜ニュートンの第1法則〜を参照してみてください。

では解答例に移りましょう。

証明

全て，エレベーターとともに運動する系で観測する。鉛直方向上向きを正にとる。

(1)おもりは静止しているように見えるから，力のつり合いより

$0 = T - 2mg$

$\therefore T =2mg$

(2)運動方程式より $ma = -2mg$

$\therefore a =-2g$

おもりは鉛直方向下向きに運動するから，おもりは床に衝突する。公式(2)より，

$0 = \dfrac{1}{2} (-2g) {t_{2}}^{2} + 0t +h =-g {t_2}^2 + h$

$\therefore t_2 =\sqrt{\dfrac{h}{g}}$

(3)運動方程式より

$ma = 3mg - mg = 2mg$

$\therefore a = 2g$

公式(3)より，

$2L = \dfrac{1}{2} (2g) {t_3}^2 +0{t_3} + h =g {t_3}^2 + h$

$\therefore t_3 = \sqrt{\dfrac{2L - h}{g}}$

(4) $t_3 > t_2$ より，

$\sqrt{\dfrac{2L - h}{g}} > \sqrt{\dfrac{h}{g}}$

$\therefore L > h$

慣性力を考慮しなければならない問題では，今自分がどの系で考えているか，常に気を遣ってください。

自由落下現象では，考える物体の質量に依らず成立するような結果を導くことができることが多々あります。最も簡単なモデルの一つですが，なかなか面白い結果です。