ドブロイ波長(物質波)の求め方

更新 2021/06/17

今回は, ド・ブロイ波(物質波)について解説します。
ド・ブロイ波(または物質波)は物質が持つ波動性を示しており, ド・ブロイ波の発見は現在の量子力学の基礎であるシュレディンガー方程式に繋がっています。
ド・ブロイ波長は　λ=hp\lambda = \dfrac{h}{p}λ=ph​ で表され, これはド・ブロイの方程式(ドブロイの式)とも呼ばれています。
本記事では, ド・ブロイ波の定義とド・ブロイ方程式の導出, そして電子が持つ波動性について詳しく解説していきます。

【英語】姉は長年ペットを飼いたいと思っています。 My sister has wanted to have a pet 2

ろ過、蒸留、分留、クロマトグラフィー、ペーパークロマトグラフィー →分離ができる再結晶、昇華法 →分離と精製ができる 3

蒸留と分留の違いを教えてください。自分で調べてみたら、蒸留は液体と固体の混合物の分離で、分留は液体と液体の混合物の分離 4

円運動についてです。問題例: ある物体が半径10mの円周上を一定の速さで運動しており、その物体が一周するのに要する時間 5

物質波というド・ブロイの仮説

光電効果や陰極線の発見,コンプトン効果などの発見により, 波として知られていた光に粒子性が発見されました。
→光電効果
→陰極線
アインシュタインは, 光は波の性質も粒子の性質も併せ持つ物質であるという光量子仮説を打ち立て, 1921年にノーベル物理学を受賞しました。
フランスの物理学者のルイ・ド・ブロイは, アインシュタインの光量子仮説の影響を受け, 逆に電子などの物質粒子には波動性があるのではないかという仮説を立て, 自身の博士論文で提案しました。
電子は単純な粒子として知られていたために, 当時の常識に反した考えでした。
ド・ブロイ波長の求め方ド・ブロイが考えた物質が持つ波はド・ブロイ波または物質波と呼ばれ, その波長をド・ブロイ波長といいます。
ド・ブロイ波長は以下のように導出ができます。
光子の運動量 ppp はコンプトン効果の解説で扱いましたが, プランク定数 hhh , 波長 λ\lambdaλ を用いて,
p=hλ
p = \dfrac{h}{\lambda}
p=λh​
となります。
→コンプトン効果
式変形をし, 運動量の式 p=mvp = mvp=mv を代入すると,
λ=hp=hmv
\lambda = \dfrac{h}{p} = \dfrac{h}{mv} 
λ=ph​=mvh​
となります。この式をド・ブロイ方程式とも呼びます。
ド・ブロイ波長(ド・ブロイ方程式)
λ=hp=hmv
\lambda = \dfrac{h}{p} = \dfrac{h}{mv} 
λ=ph​=mvh​
プランク定数 h=6.63×10−34[J⋅s]h = 6.63 \times10^{-34}\mathrm{[J  \cdot  s]}h=6.63×10−34[J⋅s]
電子の物質波の導出物質が電子の場合のド・ブロイ波長を実際に計算してみます。
電子の質量 me=9.11×10−31[kg]m_e = 9.11 \times 10^{-31}\mathrm{[kg]}me​=9.11×10−31[kg]
速さ 2.20×106[m/s]2.20 \times 10^{6} \mathrm{[m/s]}2.20×106[m/s] で飛ぶ電子の波長 λ\lambdaλ は,
λ=6.63×10−34(9.11×10−31)×(2.20×106)≃6.63×10−32.00×107≃3.32×10−10[m]
\begin{aligned}
\lambda &=  \dfrac{6.63 \times10^{-34}}{(9.11 \times 10^{-31}) \times (2.20 \times 10^{6})} \\ 
&\simeq \dfrac{6.63 \times10^{-3}}{2.00 \times 10^{7}} \\
&\simeq  3.32 \times 10^{-10} \mathrm{[m]}\\
\end{aligned}
λ​=(9.11×10−31)×(2.20×106)6.63×10−34​≃2.00×1076.63×10−3​≃3.32×10−10[m]​
と計算できます。下の図は電磁波の種類と波長の関係を示しています。
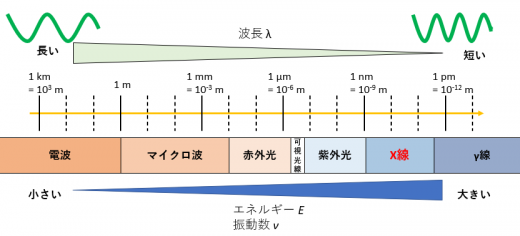
導出した電子のド・ブロイ波長はX線領域の電磁波に相当します。(X線領域：波長 λ\lambdaλ が 10−9∼10−12[m]10^{-9} \sim 10^{-12} \mathrm{[m]}10−9∼10−12[m]  程度の電磁波)
ちなみに, 電磁波とは電界と磁界の両方に作用する波のことです。
電子の流れに, 電子線(β\betaβ 線)と呼ばれるものもあります。これは, 粒子線に分類され, 電磁波とは異なります。
物質波はあらゆる物質に存在する信じがたい話かもしれませんが, ド・ブロイ波は私たちの身の回りのあらゆる物質に存在してます。私たちがキャッチボールで投げたボールも波動性を持っているということです。その場合について考えてみます。
質量 110[g]110\mathrm{[g]}110[g] のボールを速さ 20.0[m/s]20.0\mathrm{[m/s]}20.0[m/s]  で投げる場合を考えます。※質量の単位変換に注意が必要です。
λ=6.63×10−34(110×10−3)×20.0≃6.63×10−342.20≃3.01×10−34[m]
\begin{aligned}
\lambda &=  \dfrac{6.63 \times10^{-34}}{(110 \times 10^{-3}) \times 20.0} \\ 
&\simeq  \dfrac{6.63 \times10^{-34}}{2.20} \\ 
&\simeq  3.01 \times 10^{-34} \mathrm{[m]}\\
\end{aligned}
λ​=(110×10−3)×20.06.63×10−34​≃2.206.63×10−34​≃3.01×10−34[m]​
となります。計算してみると, この波長はとてつもなく短いことがわかります。電子波の波長に比べ, 102410^{24}1024 倍(1兆の二乗)も小さいです。
私たちの身の回りの物質の波動性に関して, 物質の波長が小さすぎるため, 波としての性質を考える必要がないのです。

エネルギー保存則を使ったド・ブロイ波長の求め方

エネルギー保存則を用いて, ド・ブロイ波長を求める問題は高校物理で頻出です。実際に解いてみましょう。
例
陰極に静止させた電子を電位差 VVV で加速させます。電子が陽極に到達した場合の電子波の波長 λ\lambdaλ を求めよ。
電子の電気量 −e[C]-e \mathrm{[C]}−e[C], 質量 me[kg]m_e\mathrm{[kg]}me​[kg]　とする。
解答
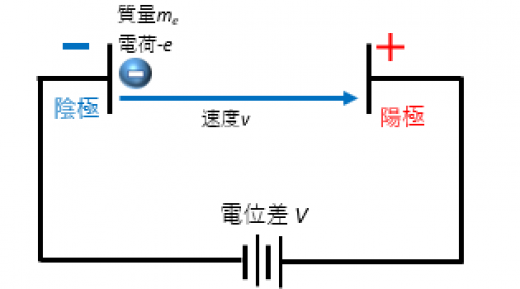
電位差 VVV の電子の位置エネルギーは, eV[J]eV\mathrm{[J]}eV[J]となる。
電子の速度を v[m/s]v \mathrm{[m/s]}v[m/s]  と置くと, 陰極から陽極まで運動する電子の運動エネルギーは, 12mev2\dfrac{1}{2}m_e v^221​me​v2 と表される。
エネルギー保存則より,
12mev2=eVmev2=2eV
\begin{aligned}
\dfrac{1}{2} m_e v^2 &= eV  \\
m_e v^2 &= 2eV \\
\end{aligned}
21​me​v2me​v2​=eV=2eV​
この式から,
v=2eVme
v =  \sqrt{\dfrac{2eV}{m_e}}  
v=me​2eV​​
が導かれる。また, 上の方程式の両辺に mem_eme​ をかけ, 運動量を pe[kg⋅m/s]p_e \mathrm{[kg \cdot m/s]}pe​[kg⋅m/s] とすると,
(mev)2=2meeVpe=mev=2meeV
\begin{aligned}
(m_ev)^2 &= 2m_e eV \\
p_e &= m_ev =  \sqrt{2m_e eV}  \\
\end{aligned}
(me​v)2pe​​=2me​eV=me​v=2me​eV​​
これをド・ブロイ波の式に代入すると,
λ=hpe=hmev=h2meeV
\lambda = \dfrac{h}{p_e} = \dfrac{h}{m_ev} = \dfrac{h}{\sqrt{2m_e eV}} 
λ=pe​h​=me​vh​=2me​eV​h​
となる。
電子のド・ブロイ波長と電位差 VVV の関係上記の問題において, 任意の電位差 VVV のときのドブロイ波長を求めることできました。具体的な電位差 VVV を代入して, 電子の波長 λ\lambdaλ がどのくらいになるか計算をしてみます。
まず, ド・ブロイ波長に定数をそれぞれ代入します。
プランク定数 : h=6.63×10−34[J⋅s]h = 6.63 \times10^{-34}\mathrm{[J  \cdot  s]}h=6.63×10−34[J⋅s]
電気素量 : e=1.60×10−19[C]e = 1.60 \times10^{-19}\mathrm{[C]}e=1.60×10−19[C]
電子の質量 : me=9.11×10−31[kg]m_e = 9.11 \times 10^{-31}\mathrm{[kg]}me​=9.11×10−31[kg]
λ=h2meeV=6.63×10−342×(9.11×10−31)×(1.60×10−19)×V=6.6322×9.11×1.60×V×10−3410−25=1.51V×10−9=151V×10−10
\begin{aligned}
\lambda &=  \dfrac{h}{\sqrt{2m_e eV}} = \dfrac{6.63 \times10^{-34}}{\sqrt{2 \times (9.11 \times 10^{-31}) \times (1.60 \times10^{-19}) \times V}} \\ 
&= \sqrt{\dfrac{6.63^2}{2 \times 9.11 \times 1.60 \times V }} \times \dfrac{10^{-34}}{10^{-25}} \\
&= \sqrt{\dfrac{1.51}{V }} \times 10^{-9} \\
&= \sqrt{\dfrac{151}{V }} \times 10^{-10} \\
\end{aligned}
λ​=2me​eV​h​=2×(9.11×10−31)×(1.60×10−19)×V​6.63×10−34​=2×9.11×1.60×V6.632​​×10−2510−34​=V1.51​​×10−9=V151​​×10−10​
ここで電位差 VVV に適当な値を代入すると,
V=100[V]V = 100 \mathrm{[V]}V=100[V]  のとき, λ≈1.23×10−10[m]\lambda \approx 1.23 \times 10^{-10}\mathrm{[m]}λ≈1.23×10−10[m]
V=1000[V]V = 1000 \mathrm{[V]}V=1000[V]   のとき, λ≈3.89×10−11[m]\lambda \approx 3.89 \times 10^{-11}\mathrm{[m]}λ≈3.89×10−11[m]
V=10000[V]V = 10000 \mathrm{[V]}V=10000[V]   のとき, λ≈1.23×10−11[m]\lambda \approx 1.23 \times 10^{-11}\mathrm{[m]}λ≈1.23×10−11[m]
どのド・ブロイ波長もX線領域の波長であることがわかります。電位差 VVV を大きくすれば, 波長 λ\lambdaλ が小さくなります。すなわち, エネルギー EEE は大きくなります。

電子の波動性についての解釈

電子は単純な粒子であると知られており, ド・ブロイの発見により電子の波動性が示されました。電子は光と同様に, 粒子性と波動性の二重性を持つ物質であるということです。
粒子性と波動性を両立する物質とは何かを考えたくなりますが, 私たちの身の回りにはありません。そのため, 電子や光は結局何なのかと考えるのは不毛なのです。
電子や光はオセロの白と黒のように, 片面に粒子性, 反対面に波動性を持つ物質なのです。それを表現したのがアインシュタインの光量子仮説です。
電子の波動性は発見確率を表す電子の波動性について理解が難しい部分があるため, 補足をしておきます。大学で扱うような発展的な内容も含みます。
電子の波動性と聞いて, 以下のような解釈をしている方がいるかもしれませんが, これらは誤りです。
電子が集団で振動した波を打つ
電子が波打ちながら振動している
これらが成り立たない理由は, 波を伝える媒質が存在しないためです。媒質は, 海の波の媒質は水, 音波の媒質は空気です。電子にはこの媒質が存在しません。
コペンハーゲンの解釈現在, 電子の波動性に関して最も主流の解釈は, コペンハーゲン解釈というものです。
コペンハーゲンの解釈
電子の波は電子の発見確率を示す。
発見確率の振幅の大きさは, 電子の発見のしやすさを表現しています。
振幅:大 → 発見確率 : 大
振幅:小 → 発見確率 : 小
コペンハーゲンの解釈では, 一つの電子は複数の場所に同時に存在しており, 電子が発見されると位置が確定します(収縮という)。 その発見しやすさを波で表現しているのです。
電子の波動性に関する議論は, 今も学者によって立場がわかれるそうです。コペンハーゲンの解釈は, 電子や光に関する実験結果を説明するのに現時点で, 最も理にかなっている解釈ということです。
ド・ブロイ波の発見は,　電子や光の波が満たすべき式が量子力学で有名なシュレディンガー方程式の原点となっています。
シュレディンガー方程式
iℏ∂∂tψ(r,t)=(−ℏ22m∇2+V(r,t))ψ(r,t)
i \hbar \dfrac{\partial}{\partial t} \psi(r,t) 
= \left(- \dfrac{\hbar^2}{2m} \nabla^2+ V(r,t) \right) \psi(r,t)
iℏ∂t∂​ψ(r,t)=(−2mℏ2​∇2+V(r,t))ψ(r,t)
量子力学におけるシュレディンガー方程式とは, 力学の運動方程式 F=maF =maF=ma くらい基本的な方程式です。