熱サイクル・熱機関・熱効率の定義と例

熱サイクル，熱機関は，熱力学では以下のように定義されます：

定義が長くなってしまいましたが，以下の文章を読みながらよく咀嚼して理解してほしいと思います。ちなみに，この記事では熱サイクルと熱機関は異なるものとして定義していますが，熱サイクルと熱機関はほぼ同じものです。言葉の定義の問題なので，混合して使われることもよくあります。

熱機関は，以下のような図を用いて描かれます。

$Q_{\text{in}}$ は温度 $T_1$ の高温な熱源から熱サイクルが吸収する熱量，$Q_{\text{out}}$ は温度 $T_2$ の低温な熱源に熱サイクルが放出する熱量です。吸収，放出が逆の場合は，マイナスの値を取れば解決します。例えば，高温な熱源に熱サイクルが熱を放出する場合は，$Q_{\text{in}}$ をマイナスの値としてとればいいわけです。

$W$ は，熱サイクルがする正味の仕事です。つまり，サイクルが外にする仕事から，サイクルを動かすのに必要な仕事を引いたものです。

熱サイクルは，理論的に多数の例が考えられています。カルノーサイクルはその1例です。この後の理論的な展開のため，カルノーサイクルについては詳しく議論を進めます。

$A,B,C,D$ という4つの状態があり， $$A \xrightarrow{\text{等温変化}} B \xrightarrow{\text{断熱変化}} C \xrightarrow{\text{等温変化}} D \xrightarrow{\text{断熱変化}} A$$ という可逆変化をする熱サイクルを，カルノーサイクルといいます。$p-V$ 図を書けば以下のようになります：

$A$ における体積，圧力を $V_A, p_A$ と書くことにします。$B,C,D$ についても同様な表記をすることにします。また，$A,B$ の温度を $T_1$，$C,D$ の温度を $T_2$ とします。

では，作業物質として $n$ モルの理想気体をつかった場合の，カルノーサイクルの各状態遷移における内部エネルギー変化，仕事，熱の出入りについて定量的に考察してみます。途中で，「状態方程式」「熱力学第一法則」については特に断りなく用います。合わせて確認してください。

• $A \to B$ の状態遷移

等温変化なので， $$\Delta U_{AB} = 0$$ です。また，正味の仕事については， $$\begin{aligned} W_{AB} &= \int_{V_A}^{V_B} p dV = \int_{V_A}^{V_B} \dfrac{nRT_1}{V} dV\\ &= nRT_1 \left[\log V\right]_{V_A}^{V_B}\\ &= nRT_1 \log \left(\dfrac{V_B}{V_A}\right) \end{aligned}$$ と計算できます。熱力学第一法則より，吸収する熱量 $Q_{\text{in}}$ は， $$Q_{\text{in}} = W_{AB}$$ と求めることができます。

• $B \to C$ の状態遷移

断熱変化なので， $$Q_{BC} = 0$$ が成立します。また， $$\Delta U_{BC} = nC_V (T_2 - T_1)$$ により，正味の仕事 $W_{BC}$ は， $$W_{BC} = \Delta U_{BC}$$ と求めることができます。

• $C \to D$ の状態遷移

$A \to B$ の変化のときと同様に議論すれば，内部エネルギーの変化，正味の仕事，放熱する熱量は，それぞれ $$\begin{aligned} \Delta U_{CD} &= 0\\ W_{CD} &= nRT_2 \log \left(\dfrac{V_D}{V_C}\right)\\ Q_{\text{out}} &= -W_{CD} \end{aligned}$$ と計算することができます。

• $D \to A$ の状態遷移

$B \to C$ の変化のときと同様に議論すれば，放熱する熱量，内部エネルギーの変化，正味の仕事は，それぞれ $$\begin{aligned} Q_{DA} &= 0\\ \Delta U_{DA} &= nC_V (T_1 - T_2)\\ W_{DA} &= -\Delta U_{DA} \end{aligned}$$ と計算することができます。

逆カルノーサイクル

カルノーサイクルにおける状態遷移は可逆変化なので，理論的にはカルノーサイクルの真逆の変化をたどる熱サイクルを考えることができます。この熱サイクルを逆カルノーサイクルと呼ぶことがあります。

前節で計算したことの真逆なので，温度 $T_2$ の低温な熱源から熱サイクルが吸収する熱量を $Q'_{\text{in}}$，温度 $T_1$ の高温な熱源に熱サイクルが放出する熱量を $Q'_{\text{out}}$，サイクルがされる仕事を $W'$ とすると， $$\begin{aligned} Q_{\text{in}} &= Q'_{\text{out}}\\ Q_{\text{out}} &= Q'_{\text{in}}\\ W &= W' \end{aligned}$$ となります（もちろん前節のように真面目に計算しても良いです）。

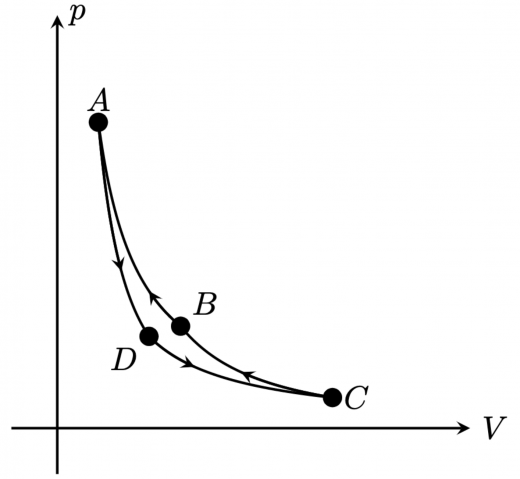
つまり，サイクルに仕事を与えることで，低温な熱浴から熱を奪い，さらに温度を下げることができるような装置ができる わけです。この機構は，クーラーや冷蔵庫の原理になっています。

オットーサイクル

カルノーサイクルの他にも，オットーサイクルと呼ばれる熱サイクルがあります。

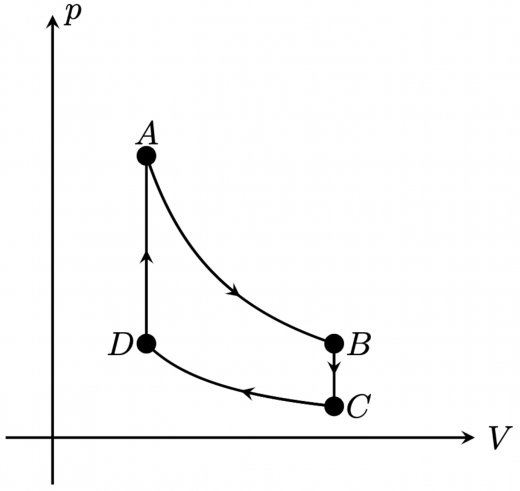
$A,B,C,D$ という4つの状態があり， $$A \xrightarrow{\text{断熱変化}} B \xrightarrow{\text{定積変化}} C \xrightarrow{\text{断熱変化}} D \xrightarrow{\text{定積変化}} A$$ という変化をする熱サイクルを，オットーサイクルといいます。p-V図を書けば以下のようになります：

スターリングサイクル

$A,B,C,D$ という4つの状態があり， $$A \xrightarrow{\text{等温変化}} B \xrightarrow{\text{定積変化}} C \xrightarrow{\text{等温変化}} D \xrightarrow{\text{定積変化}} A$$ という変化をする熱サイクルを，スターリングサイクルといいます。p-V図を書けば以下のようになります：

熱サイクルの性能を記述する量の代表例として，熱効率というものがあります。

1サイクルで取り込んだ熱量のうち，どれくらいの割合を正味の仕事に変換することができるかを表すのが，熱サイクルの熱効率です。

例として，理想気体を作業物質としたカルノーサイクルの熱効率を求めてみます。

1サイクルにおける内部エネルギー変化は $0$ ですから， $$W = Q_{\text{in}} - Q_{\text{out}}$$ が成立します。これにより， $$\begin{aligned} \eta &= \dfrac{W}{Q_{\text{in}}} = \dfrac{Q_{\text{in}} - Q_{\text{out}}}{Q_{\text{in}}}\\ &= 1 - \dfrac{Q_{\text{out}}}{Q_{\text{in}}} \end{aligned}$$

さて，断熱変化において，次の公式が成立します：

この式の証明は別の記事→断熱変化におけるポアソンの式の導出で紹介しています（圧力 $p$ を状態方程式で消去すれば，記事の式と上の式は同じ式になります）。大学入試等では，ポアソンの式は一応範囲外であり，出題されるとしても既知の公式として問題文に与えられることが多いです。

ポアソンの式から，カルノーサイクルにおいて， $$\begin{aligned} \begin{cases} T_1 V_A^{\gamma -1} = T_2 V_D^{\gamma-1}\\ T_1 V_B^{\gamma -1} = T_2 V_C^{\gamma-1} \end{cases} \end{aligned}$$ が成立するので， $$\dfrac{V_B}{V_A} = \dfrac{V_C}{V_D}$$ が導けます。これを用いると， $$\begin{aligned} \eta &= 1 - \dfrac{Q_{\text{out}}}{Q_{\text{in}}}\\ &= 1 - \dfrac{-nRT_2 \log \left(\dfrac{V_D}{V_C}\right)}{nRT_1 \log \left(\dfrac{V_B}{V_A}\right)}\\ &= 1 - \dfrac{nRT_2 \log \left(\dfrac{V_C}{V_D}\right)}{nRT_1 \log \left(\dfrac{V_B}{V_A}\right)}\\ &= 1 - \dfrac{T_2}{T_1} \end{aligned}$$ が成立します。

実は，この熱効率の値は，理想気体を作業物質としなくても成立する値であり，任意の熱機関はこの熱効率を超えることができない ことが，後に示されます。

これで熱力学第二法則を理解するための準備ができました。

この後，「トムソンの原理」「クラウジウスの原理」「オストヴァルトの原理」という概念が出てきます。これらは全て同値であることが証明できます。これらのうちの一つを原理として認めれば，それがあなたの熱力学における「熱力学第二法則」ということになります。

さらにこれらの原理から，「カルノーの定理」という定理を導くことができます。これは，「任意のサイクルの熱効率が，カルノーサイクルの熱効率を超えない」ということを主張する定理です。つまり，カルノーサイクル以上の熱効率を持つ熱サイクルを創りだすことは理論的にできないということです。