ボイル・シャルルの法則と状態方程式

理想気体について，一般に次の法則が知られています。

上記2式をまとめてボイル・シャルルの法則といいます。

ボイルの法則

ボイルの法則は，気体を等温変化させた時，その圧力と体積が反比例することを示したものです。

以下のようなシリンダーに閉じ込められた気体分子を考えると，直感的に理解しやすいでしょう。温度一定の下で，シリンダーにかける圧力を2倍，3倍と大きくしていくと、体積が1/2倍，1/3倍と小さくなっていきます。

シャルルの法則

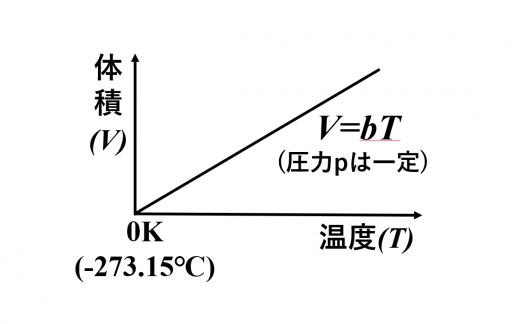
シャルルの法則は，気体を定圧変化させた時，その体積と温度が比例することを示したものです。

ここでもシリンダーに閉じ込められた気体分子をイメージしてみましょう。圧力一定のもとで，気体分子の温度を2倍，3倍とすると，体積も2倍，3倍となります。温めると体積が大きくなるのは，気体分子の熱運動が大きくなるからです。

なお、この時の「温度」とは絶対温度（$\mathrm{K}$）のことです。セルシウス温度（$^\circ$C）ではないので注意しましょう。（気温が10$^\circ$Cから20$^\circ$Cになっただけで体積が2倍になってしまっては，明らかに日常生活に支障をきたしてしまいますね。）

ボイル・シャルルの法則の導出

ボイルの法則とシャルルの法則から，ボイル・シャルルの法則を導出します。

ボイル・シャルルの法則 $\dfrac{PV}{T}=const$ において，$const$ は $n$ に比例することが分かりました。つまり，$$\dfrac{PV}{T}=nR　（R：比例定数）$$

これを整理して，理想気体の状態方程式が得られます。

ここで $R$ を気体定数といい，$$R=8.31\times10^{3} [\dfrac{\mathrm{Pa}\cdot \ell}{\mathrm{mol}\cdot\mathrm{K}}]$$

なお，実在気体において近似的に状態方程式を利用する際は，質量を $m$，気体の分子量を $M$ として，$$PV=\dfrac{m}{M}RT$$と表すこともあります。

状態方程式から導かれる数値や性質は多いです。

例えば，標準状態（1気圧 $0[\mathrm{K}]$の状態）での理想気体 $1\mathrm{mol}$ あたりの体積$V_0$は，状態方程式より $$V_0\fallingdotseq\ \dfrac{1[\mathrm{mol}]\times8.31\times10^{3}[\dfrac{\mathrm{Pa}\cdot \ell}{\mathrm{mol}\cdot\mathrm{K}}]\times273[\mathrm{K}]}{1.01\times10^{5}[\mathrm{Pa}]}\fallingdotseq22.4[\ell]$$

他にも，断熱変化におけるポアソンの式なども，状態方程式より導出することができます。

ボイルの法則もシャルルの法則も，理想気体においてのみ成り立ちます。当然，これら2式をまとめたボイル・シャルルの法則も，そこから導かれる状態方程式も同様です。

理想気体とは体積が $0$ で，分子間力が働かない気体のことを指します。理想気体は現実には存在しません。

現実に存在する気体のことを，理想気体に対して実在気体と呼びます。実在気体においては、ボイル・シャルルの法則や状態方程式は成り立ちませんが，気体が理想気体に近い振る舞いをする条件下では，$\dfrac{PV}{nRT}$ の値が1に近づきます（理想気体では $\dfrac{PV}{nRT}=1$）。

実在気体において，$\dfrac{PV}{nRT}$ の値が1より小さい時は，主に分子間力が原因です。分子間力により実在気体分子同士が引き合うことで，体積 $V$ が小さくなるからです。

$\dfrac{PV}{nRT}$ の値が1より大きい時は，主に分子の体積が原因です。高圧条件下では実在気体の分子体積が無視できなくなり，体積 $V$ が大きくなるからです。

なお，高温低圧下においては，分子間力や実在気体の体積の影響が小さくなるので，$\dfrac{PV}{nRT}$ の値が1に近づきます。