ベクトル場における発散（div）と回転（rot）の定義・意味

あるベクトル $\boldsymbol{A}$ が空間上の各点 $(x,y,z)$ で定義されているとき，$\boldsymbol{A}(x,y,z)$ をベクトル場といいます。

たとえば，流体の速度や磁石の周りの磁力線がベクトル場です。

空間微分演算子 $\nabla$（ナブラ）は次のように定義されます。

数学的に何かに作用するものを演算子とよびます。 たとえば $\partial_x \coloneqq \dfrac{\partial}{\partial x}$ も微分演算子で，関数 $f(x,y,z)$ に作用させると $\partial_xf=\dfrac{\partial f}{\partial x}$ となるといった具合です（ふつう微分演算子は右へ作用します）。微分演算子に限らず，$a[f(x)] \coloneqq af(x)$ と定義したときの $a[\cdot]$ も演算子と言えるでしょう。 演算子の中には複数の対象を引数にとるものもあります（たとえば二項係数 ${}_n\mathrm{C}_r$ は二項演算子です）。

空間微分演算子 $\nabla$ がスカラー場 $f(x,y,z)$ に作用したものは勾配（gradient）といい， $\nabla f(x,y,z) = \left(\dfrac{\partial{f}}{\partial{x}},\dfrac{\partial{f}}{\partial{y}},\dfrac{\partial{f}}{\partial{z}}\right)$ となります。→勾配ベクトルの意味と例題

ベクトル場の発散（divergence）の定義は以下の通りです。

ここで登場した $\mathrm{div}$ も演算子で，右にあるベクトル場に作用します。

たとえば，ベクトル場 $\boldsymbol{A}(x,y,z)=(xy,yz,zx)$ の発散は， $$\begin{aligned} \mathrm{div}\,\boldsymbol{A}(x,y,z) &=\dfrac{\partial{}}{\partial{x}}(xy)+\dfrac{\partial{}}{\partial{y}}(yz)+\dfrac{\partial{}}{\partial{z}}(zx)\\ &=y+z+x \end{aligned}$$ となります。

発散の物理的な意味を考えてみましょう。 ベクトル場の例として流体の流量 $\boldsymbol{V}(x,y,z)$ を考えてみます。点 $(x,y,z)$ から $\boldsymbol{V}$ の方向に単位面積当たり $V=|\boldsymbol{V}|$ の量だけ流体が流れ出ているイメージです。

ある点 $(x,y,z)$ での流体の増減を調べることにします。 点での増減を直接調べるのは難しいので，点 $(x,y,z)$ を中心とする下図のような非常に小さな直方体を考えましょう（$\varDelta x,\varDelta y,\varDelta z\ll1$）。後々 $\varDelta x,\varDelta y,\varDelta z\to0$ の極限を取ることで点 $(x,y,z)$ での増減を調べます。

まず，$x$ 方向に垂直な面の流入・流出を考えます。 点 $(x\pm\varDelta x/2,y,z)$ における $x$ 方向の（単位面積あたりの）流量は $V_x(x\pm\varDelta x/2,y,z)$ なので， この面を通過する流量を $V_x(x\pm\varDelta x/2,y,z)\varDelta y\varDelta z$ と近似してやります。 $$\begin{aligned} &\quad\int_{y-\varDelta y/2}^{y+\varDelta y/2}\int_{z-\varDelta z/2}^{z+\varDelta z/2} V_x\left(x\pm\dfrac{\varDelta x}{2},y,z\right)\,dy\,dz\\ &\simeq V_x\left(x\pm\dfrac{\varDelta x}{2},y,z\right)\varDelta y\varDelta z \end{aligned}$$ $\varDelta y,\varDelta z$ は極めて小さいので，面上での $V_x$ を一点の値として近似しています。

これを Taylor 展開して $\varDelta x$ の１次まで近似すると， $$\begin{aligned} &\quad V_x\left(x\pm\dfrac{\varDelta x}{2},y,z\right) \\ &=V_x(x,y,z)\pm\dfrac{\partial{V_x(x,y,z)}}{\partial{x}}\frac{\varDelta x}{2}+\dfrac{1}{2}\dfrac{\partial^2{V_x(x,y,z)}}{\partial{x}^2}\left(\frac{\varDelta x}{2}\right)^2+\cdots\\ &\simeq V_x(x,y,z)\pm\dfrac{\partial{V_x(x,y,z)}}{\partial{x}}\frac{\varDelta x}{2} \end{aligned}$$ となります（Taylor 展開についてはテイラーの定理とテイラー展開～例と証明を参照）。 正味の流量変化は， $$\begin{aligned} &\quad\left[ V_x \left(x+ \dfrac{\varDelta x}{2},y,z\right) -V_x\left(x-\dfrac{\varDelta x}{2},y,z\right)\right] \varDelta y\varDelta z \\ &=\left[\left(V_x+\frac{\partial V_x}{\partial x}\frac{\varDelta x}{2}\right)-\left(V_x-\frac{\partial V_x}{\partial x}\frac{\varDelta x}{2}\right)\right]\varDelta y\varDelta z\\ &=\dfrac{\partial{V_x}}{\partial{x}}\varDelta x\varDelta y\varDelta z \end{aligned}$$ となります。同様の計算を $y$ 方向に垂直な２面，$z$ 方向に垂直な２面にも適応すると，正味の流量変化はそれぞれ $\dfrac{\partial{V_y}}{\partial{y}}\varDelta x\varDelta y\varDelta z, \dfrac{\partial{V_z}}{\partial{z}}\varDelta x\varDelta y\varDelta z$ となるので，３方向の正味の流量変化は， $$\left( \dfrac{\partial{V_x}}{\partial{x}}+\dfrac{\partial{V_y}}{\partial{y}}+\dfrac{\partial{V_z}}{\partial{z}} \right)\varDelta x\varDelta y\varDelta z$$ となります。$\boldsymbol{V}$ の発散の因子 $\nabla\cdot\boldsymbol{V}$ が出てきたことに気づいたと思います。$\nabla\cdot\boldsymbol{V}$ を用いて正味の流入変化を書き換えると $\nabla\cdot\boldsymbol{V}\varDelta x\varDelta y\varDelta z$ と表せます。

つまり，発散 $\nabla\cdot\boldsymbol{V}$ はその点における単位体積当たりの流量変化を表しているとわかります。

$\nabla\cdot\boldsymbol{V}>0$ の点では流体が湧き出しています（湧き出し）。 逆に $\nabla\cdot\boldsymbol{V}<0$ の点では流体を吸い込んでいます（吸い込み）。 $\nabla\cdot\boldsymbol{V}=0$ の点では湧き出しも吸い込みもないことになります。

ベクトル場の回転（rotation）の定義は以下の通りです。

たとえば，発散の例と同じベクトル場 $\boldsymbol{A}(x,y,z)=(xy,yz,zx)$ の回転は， $$\begin{aligned} \mathrm{rot}\,\boldsymbol{A} &=\left(\dfrac{\partial{}}{\partial{y}}(zx)-\dfrac{\partial{}}{\partial{z}}(yz),\dfrac{\partial{}}{\partial{z}}(xy)-\dfrac{\partial{}}{\partial{x}}(zx),\dfrac{\partial{}}{\partial{x}}(yz)-\dfrac{\partial{}}{\partial{y}}(xy)\right)\\ &=(0-y,0-z,0-x)\\ &=(-y,-z,-x) \end{aligned}$$ となります。

回転の物理的な意味を考えてみましょう。 発散の場合と同様に，ベクトル場の例として流体の流れ $\boldsymbol{V}(x,y,z)$ を考えます。

ある点 $(x,y,z)$ を中心として流体の回転の度合いを計算してみます。 下図のように，点 $(x,y,z)$ を中心とする $xy$ 平面に平行で非常に小さな長方形を考えます（$\varDelta x,\varDelta y\ll1$）。

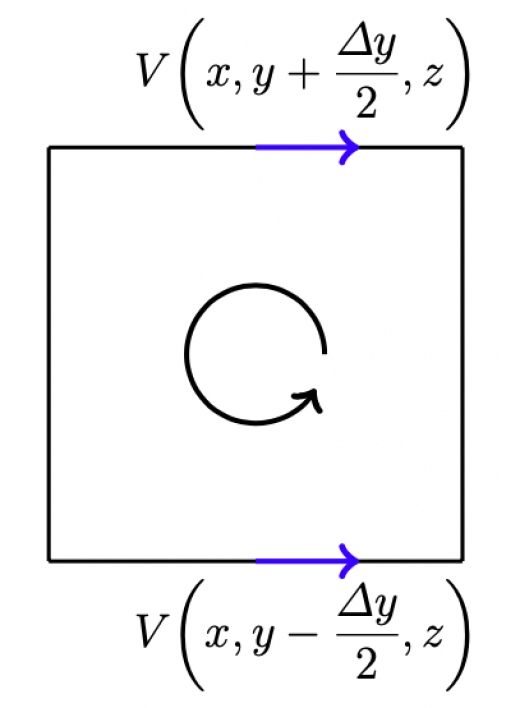
まず $x$ 方向に沿った流れを計算します。 回転を考えたいので，$y=y+\varDelta y$ では $x$ 正の方向を負の回転，$y=y-\varDelta y$ では $x$ 正の方向を正の回転と考えることにします。 点 $(x,y\pm\varDelta y/2,z)$ における $x$ 方向に沿った流れは $V_x(x,y\pm\varDelta y/2,z)$ なので， $y=y\pm\varDelta y$ の線に沿った回転量を $\mp V_x(x,y\pm\varDelta y/2,z)\varDelta x$ に近似します。 $$\int_{x-\varDelta x/2}^{x+\varDelta x/2} V_x\left(x,y\pm\dfrac{\varDelta y}{2},z\right)\,dx \simeq V_x\left(x,y\pm\dfrac{\varDelta y}{2},z\right)\varDelta x$$ $\varDelta x$ は極めて小さいので，線上での $V_x$ を一点の値として近似しています。

これを Taylor 展開して $\varDelta y$ の１次まで近似すると， $$\begin{aligned} &\quad V_x\left(x,y\pm\dfrac{\varDelta y}{2},z\right)\\ &=V_x(x,y,z) \pm\dfrac{\partial{V_x(x,y,z)}}{\partial{y}}\frac{\varDelta y}{2} +\dfrac{1}{2}\dfrac{\partial^2{V_x(x,y,z)}}{\partial{y}^2}\left(\frac{\varDelta y}{2}\right)^2 +\cdots\\ &\simeq V_x(x,y,z) \pm\dfrac{\partial{V_x(x,y,z)}}{\partial{y}}\frac{\varDelta y}{2} \end{aligned}$$ となるので，正味の回転量は， $$\begin{aligned} &\quad \left[ -V_x\left(x,y+\dfrac{\varDelta y}{2},z\right) +V_x\left(x,y-\dfrac{\varDelta y}{2},z\right)\right] \varDelta x \\ &=-\left[ \left(V_x+\frac{\partial V_x}{\partial y}\frac{\varDelta y}{2}\right) -\left(V_x-\frac{\partial V_x}{\partial y}\frac{\varDelta y}{2} \right) \right]\varDelta x\\ &=-\dfrac{\partial{V_x}}{\partial{y}}\varDelta x\varDelta y \end{aligned}$$ となります。同様の計算を $y$ 方向に沿った２本の経路にも適応すると，正味の回転量は $\dfrac{\partial{V_y}}{\partial{x}}\varDelta x\varDelta y$ となります。$y$ に沿った方向では $x=x+\varDelta x/2$ で $y$ 正の方向を正の回転，$x=x-\varDelta x/2$ で $y$ 正の方向を負の回転とするので，回転量の符号が変わることに気をつけてください。したがって４辺の正味の回転量は， $$\left( \dfrac{\partial{V_y}}{\partial{x}}-\dfrac{\partial{V_x}}{\partial{y}} \right)\varDelta x\varDelta y$$ となります。今度は $\boldsymbol{V}$ の回転の $z$ 成分 $(\nabla\times\boldsymbol{V})_z$ が出てきました。$(\nabla\times\boldsymbol{V})_z$ を用いて正味の回転量を書き換えると $(\nabla\times\boldsymbol{V})_z\varDelta x\varDelta y$ と表せます。 $yz$ 平面，$zx$ 平面上の回転量も同様に $(\nabla\times\boldsymbol{V})_x\varDelta y\varDelta z, (\nabla\times\boldsymbol{V})_y\varDelta z\varDelta x$ となります。

つまり，回転 $\nabla\cdot\boldsymbol{V}$ はその点まわりの（単位面積あたりの）物理的な回転を表していることがわかります。

回転 $\nabla\times\boldsymbol{V}$ はベクトルなので，スカラーである回転量と対応しないのではという疑問を抱いた方もいるかもしれません。 例えば，ベクトル $\boldsymbol{n}$ に垂直で面積が $\varDelta S$ の平面を考えると，その平面上での回転量は $(\nabla\times\boldsymbol{V})\cdot \varDelta S\boldsymbol{n}$ と表されます。先の導出では $\boldsymbol{n}$ を $\boldsymbol{e}_z$ に取ることに対応します（実際に $xy$ 平面を考えていました）。$\boldsymbol{n}$ を変化させたときに回転量 $(\nabla\times\boldsymbol{V})\cdot \varDelta S\boldsymbol{n}$ が最大になるのは $\boldsymbol{n}$ が $\nabla\times\boldsymbol{V}$ と平行なときです。

例1：回転が0になる例

ベクトル場として $\boldsymbol{V}(x,y,z)=(x,y,z)$ を考えます。 発散と回転を計算すると次の通りです。 $$\begin{aligned} \nabla\cdot\boldsymbol{V} &=\dfrac{\partial{}}{\partial{x}}x+\dfrac{\partial{}}{\partial{y}}y+\dfrac{\partial{}}{\partial{z}}z =3\\ \nabla\times\boldsymbol{V} &=\left( \dfrac{\partial{}}{\partial{y}}z-\dfrac{\partial{}}{\partial{z}}y, \dfrac{\partial{}}{\partial{z}}x-\dfrac{\partial{}}{\partial{x}}z, \dfrac{\partial{}}{\partial{x}}y-\dfrac{\partial{}}{\partial{y}}x \right) =(0,0,0) \end{aligned}$$

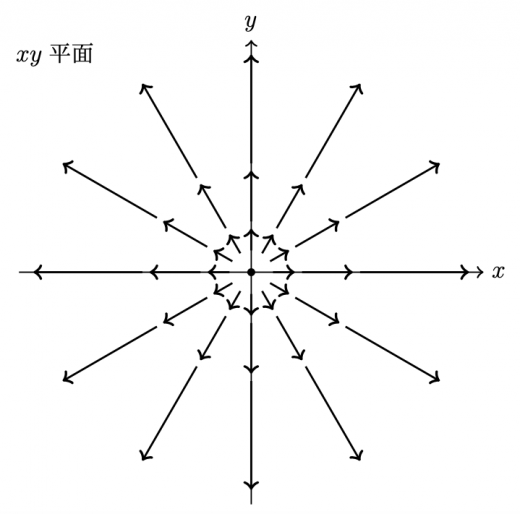
物理的な意味を考えましょう。ベクトル場は下の図のようになっています。 原点から広がるようなベクトル場になっており，離れれば離れるほど $V=|\boldsymbol{V}|$ は大きくなります。 発散は $\nabla\cdot\boldsymbol{V}=3$ なので，空間上すべての点で等しい湧き出しが生じています。 一方で $\nabla\times\boldsymbol{V}=\boldsymbol{0}$ なので，回転がどこにも存在していないということになります。

例2：発散が0になる例

ベクトル場として $V(x,y,z)=(-y,-z,-x)$ を考えます。 発散と回転は次のように計算できます。 $$\begin{aligned} \nabla\cdot\boldsymbol{V} &=\dfrac{\partial{}}{\partial{x}}(-y)+\dfrac{\partial{}}{\partial{y}}(-z)+\dfrac{\partial{}}{\partial{z}}(-x) =0\\ \nabla\times\boldsymbol{V} &=\left( \dfrac{\partial{}}{\partial{y}}(-x)-\dfrac{\partial{}}{\partial{z}}(-z), \dfrac{\partial{}}{\partial{z}}(-y)-\dfrac{\partial{}}{\partial{x}}(-x), \dfrac{\partial{}}{\partial{x}}(-z)-\dfrac{\partial{}}{\partial{y}}(-y) \right)\\ &=(1,1,1) \end{aligned}$$ 例１とは反対に，発散が $\nabla\cdot\boldsymbol{V}=0$ なので，どの点においても湧き出しが生じていないということになります。回転は $\nabla\times\boldsymbol{V}=(1,1,1)$ となり，例えば $z$ 平面に平行な面を考えると，$(\nabla\times\boldsymbol{V})\cdot{\boldsymbol{e}}_z=1$ なので正の方向（反時計回り）に回転が生じていることがわかります。

２次元空間上の発散と回転

いままでは３次元の $xyz$ 空間を考えてきましたが，２次元の $(x,y)$ 平面でも発散と回転を定義することができます（３次元の場合で $z=0, A_z(x,y,0)=0$ とした場合に対応します）。

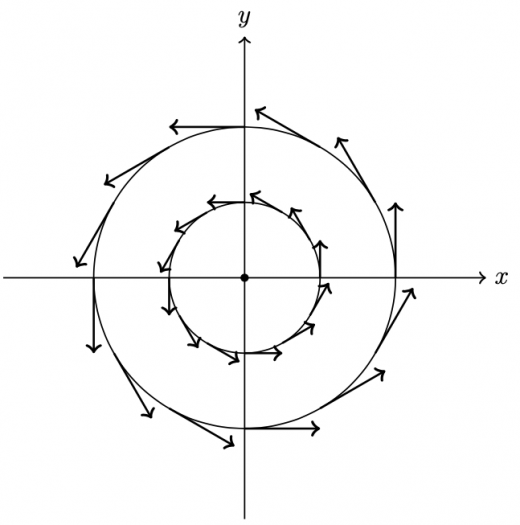
具体例 $\boldsymbol{V}=(-y,x)$ を用いて発散と回転を計算してみましょう。 $$\begin{aligned} \mathrm{div}\,\boldsymbol{V} &=\dfrac{\partial{}}{\partial{x}}(-y)+\dfrac{\partial{}}{\partial{y}}x =0\\ \mathrm{rot}\,\boldsymbol{V} &=\left( \dfrac{\partial{}}{\partial{x}}x-\dfrac{\partial{}}{\partial{y}}(-y)\right){\boldsymbol{e}}_z =2{\boldsymbol{e}}_z \end{aligned}$$ 図を見ると回転になっていることが容易にわかると思います。