ガウスの発散定理・ストークスの定理の証明

まずはガウスの発散定理を証明します。やや長いので，4ステップに分けて1つずつ説明します。

閉曲面の面積分は分割できる

まず，閉曲面を2分割したものの面積分の和が，もとの閉曲面の面積分に等しいことを述べます。

$\boldsymbol{A}$ の任意の閉曲面 $S$ に対する面積分： $$\int_S \boldsymbol{A} \cdot \boldsymbol{n} dS$$ を考えます。

閉曲面 $S$ を，$S_{\text{中}}$ という平面で，$S_{\text{左}}$ と $S_{\text{右}}$ という曲面に分割します。また，$S_{\text{中}}$ に対し，図のように単位法線ベクトルを用意します。

このとき， $$\begin{aligned} \int_{S_{\text{左}} + S_{\text{中}}} \boldsymbol{A} \cdot \boldsymbol{n} dS &= \int_{S_{\text{左}}} \boldsymbol{A} \cdot \boldsymbol{n} dS + \int_{S_{\text{中}}} \boldsymbol{A} \cdot \boldsymbol{n_{\text{右}}} dS\\ \int_{S_{\text{右}} + S_{\text{中}}} \boldsymbol{A} \cdot \boldsymbol{n} dS &= \int_{S_{\text{右}}} \boldsymbol{A} \cdot \boldsymbol{n} dS + \int_{S_{\text{中}}} \boldsymbol{A} \cdot \boldsymbol{n_{\text{左}}} dS \end{aligned}$$ が成立します。

単位法線ベクトル $\boldsymbol{n_{\text{左}}}, \boldsymbol{n_{\text{右}}}$ は大きさが同じ，向きが真逆のベクトルなので，同じ面に対する面積分は和をとると打ち消し合います。つまり， $$\int_{S_{\text{中}}} \boldsymbol{A} \cdot \boldsymbol{n_{\text{左}}} dS + \int_{S_{\text{中}}} \boldsymbol{A} \cdot \boldsymbol{n_{\text{右}}} dS = 0$$ です。よって， $$\begin{aligned} &\int_{S_{\text{左}} + S_{\text{中}}} \boldsymbol{A} \cdot \boldsymbol{n} dS + \int_{S_{\text{右}} + S_{\text{中}}} \boldsymbol{A} \cdot \boldsymbol{n} dS \\&= \int_{S_{\text{左}}} \boldsymbol{A} \cdot \boldsymbol{n} dS + \int_{S_{\text{右}}} \boldsymbol{A} \cdot \boldsymbol{n} dS \\&= \int_S \boldsymbol{A} \cdot \boldsymbol{n} dS \end{aligned}$$ ここで $S_{\text{左}} + S_{\text{中}}$ という閉曲面を $S_1$，$S_{\text{右}} + S_{\text{中}}$ という閉曲面を $S_2$で表すと， $$\int_{S_1} \boldsymbol{A} \cdot \boldsymbol{n} dS + \int_{S_2} \boldsymbol{A} \cdot \boldsymbol{n} dS = \int_S \boldsymbol{A} \cdot \boldsymbol{n} dS \tag{*}$$ です。この式 $(*)$ はとても重要で，「任意の閉曲面 $S$ における $\boldsymbol{A}$ の面積分は，それを分割したときにできる2つの閉曲面 $S_1, S_2$ における $\boldsymbol{A}$ の面積分の和に等しい」ことを表しています。面積分を考える上では，好きなように閉曲面を分割して良いということです。

微小立方体の集合として考える

前節で見たように，閉曲面の面積分は分割して考えられます。そこで，分割を繰り返して $S$ を極限まで切り刻んでみましょう。具体的には，$S$ とその中身を十分たくさんの微小立方体 $S_1, S_2, \cdots, S_N$ を合わせたもので近似します。（$S$ と $\boldsymbol{A}$ が滑らかなら）$N\to\infty$ とすれば近似はいくらでも正確になります。

つまり，面積分について， $$\int_S \boldsymbol{A} \cdot \boldsymbol{n}dS = \lim_{N \to \infty}\left\{\sum_{i = 1}^N \int_{S_i} \boldsymbol{A} \cdot \boldsymbol{n} dS\right\}$$ が成立します。

任意の閉曲面の面積分が微小立方体の面積分の総和で置き換えられました。

微小立方体の面積分を考える

では，微小立方体の6面を閉曲面とする面積分を考えてみましょう。下図のように，法線ベクトルに名前をつけます。また，$\boldsymbol{n_A}$ に対応する面の名前を $S_A$，$\boldsymbol{n_B}$ に対応する面の名前を $S_B$ のように呼ぶことにします。

この微小立方体の6面を合わせて $S_i$ と呼ぶことにすると， $$\int_{S_i} \boldsymbol{A} \cdot \boldsymbol{n} dS = \sum_{\text{面}\in\{A,B,C,D,E,F\}}\int_{S_{\text{面}}}\boldsymbol{A} \cdot \boldsymbol{n_{\text{面}}} dS$$ と計算することができます。

まず，面 $A$ と面 $F$ の寄与を考えます。 $$\begin{aligned} &\int_{S_A} \boldsymbol{A} \cdot \boldsymbol{n_A} dS\\ &\approx \left(\begin{array}{c} A_x\left(x + \dfrac{\Delta x}{2},y + \dfrac{\Delta y}{2}, z + \Delta z\right)\\ A_y\left(x + \dfrac{\Delta x}{2},y + \dfrac{\Delta y}{2}, z + \Delta z\right)\\ A_z\left(x + \dfrac{\Delta x}{2},y + \dfrac{\Delta y}{2}, z + \Delta z\right)\\ \end{array}\right) \cdot \left(\begin{array}{c} 0\\ 0\\ 1 \end{array}\right) \Delta x \Delta y\\ &= A_z \left(x + \dfrac{\Delta x}{2},y + \dfrac{\Delta y}{2}, z + \Delta z\right)\Delta x \Delta y \end{aligned}$$ また， $$\begin{aligned} &\int_{S_F} \boldsymbol{A} \cdot \boldsymbol{n_F} dS \\&\approx \left(\begin{array}{c} A_x\left(x + \dfrac{\Delta x}{2},y + \dfrac{\Delta y}{2}, z\right)\\ A_y\left(x + \dfrac{\Delta x}{2},y + \dfrac{\Delta y}{2}, z\right)\\ A_z\left(x + \dfrac{\Delta x}{2},y + \dfrac{\Delta y}{2}, z\right)\\ \end{array}\right) \cdot \left(\begin{array}{c} 0\\ 0\\ -1 \end{array}\right) \Delta x \Delta y\\ &= - A_z \left(x + \dfrac{\Delta x}{2},y + \dfrac{\Delta y}{2}, z\right)\Delta x \Delta y \end{aligned}$$ 面 $A$ と面 $F$ の寄与はこれらの和であり， $$\begin{aligned} &\Delta x \Delta y \left(A_z \left(x + \dfrac{\Delta x}{2},y + \dfrac{\Delta y}{2}, z + \Delta z\right) - A_z \left(x + \dfrac{\Delta x}{2},y + \dfrac{\Delta y}{2}, z\right) \right)\\ &\approx \Delta x \Delta y \left(\left. \dfrac{\partial{A_z}}{\partial{z}} \right|_{x = x + \frac{\Delta x}{2}, y + \frac{\Delta y}{2}, z}\right) \Delta z\\ &= \Delta x \Delta y \left(\dfrac{\partial{A_z}}{\partial{z}} + \left(\dfrac{\Delta x}{2} \text{によるズレ}\right) + \left(\dfrac{\Delta y}{2} \text{によるズレ}\right)\right) \Delta z\\ &\approx \dfrac{\partial{A_z}}{\partial{z}}\Delta x \Delta y \Delta z \end{aligned}$$ ただし，最後の行の変形について，$\left(\dfrac{\Delta x}{2} \text{によるズレ}\right) + \left(\dfrac{\Delta y}{2} \text{によるズレ}\right)$ が $\dfrac{\partial A_z}{\partial z}$ と比べて微小なため無視しました。

同様に $B,D$ の寄与と $C,E$ の寄与も考えて足すと， $$\begin{aligned} \int_{S_i} \boldsymbol{A} \cdot \boldsymbol{n} dS &= \left(\dfrac{\partial{A_x}}{\partial{x}} + \dfrac{\partial{A_y}}{\partial{y}} + \dfrac{\partial{A_z}}{\partial{z}}\right)\Delta x \Delta y \Delta z\\ &= \nabla \cdot \boldsymbol{A} \Delta x \Delta y \Delta z\\ &= \nabla \cdot \boldsymbol{A} \Delta V \end{aligned}$$ これで，微小立方体の面積分を求めることができました。

もとの式に代入する

微小立方体の結果をもとの式に代入するだけです。任意の閉曲面における面積分は $$\int_S \boldsymbol{A} \cdot \boldsymbol{n} dS = \lim_{N \to \infty}\left\{\sum_{i = 1}^N\nabla \cdot \boldsymbol{A} \Delta V \right\}$$ 右辺を体積積分で置き換えてあげると， $$\int_S \boldsymbol{A} \cdot \boldsymbol{n} dS = \int_V \nabla \cdot \boldsymbol{A} dV$$ となり，証明終了です。

ガウスの発散定理： $$\int_S \boldsymbol{A} \cdot \boldsymbol{n} dS = \int_V \nabla \cdot \boldsymbol{A} dV$$ の大雑把なイメージを紹介します。

面積が $dS$ であるような微小曲面を，ベクトル場 $\boldsymbol{A}$ が横切っている状況を考えます。

このとき， $$\boldsymbol{A} \cdot \boldsymbol{n} dS$$ という量を考えます。$\boldsymbol{A}$ が水の流れのようなものだと思えば，この量は単位時間あたりに $dS$ を貫く水の量を表します。これを，曲面 $S$ にそって面積分したもの： $$\int_S \boldsymbol{A} \cdot \boldsymbol{n} dS$$ は，$S$ という曲面を単位時間あたりに貫く水の量を表すことになります。これを流束と呼ぶことがあります。とくに $S$ が閉曲面である場合には，$S$ という囲いから，単位時間あたりに溢れ出す水の総量を表しているわけです。

これに対し，発散： $$\nabla \cdot \boldsymbol{A} = \mathrm{div} \boldsymbol{A}$$ は，単位体積あたりの湧き出し，吸い込みを表す量です（これの説明は少し時間がかかるので，この記事では説明しません。この記事の証明が読めていれば，理解するのは全然難しくありませんので，気になる方は調べてみると良いでしょう）。つまり， $$\int_V \nabla \cdot \boldsymbol{A} dV$$ は $V$ という立体における単位体積あたりの湧き出し，吸い込みを表す量であると考えられます。

つまり，ガウスの発散定理は，以下の2つが等しいことを表しています。

• 閉曲面 $S$ を貫く水の総量（左辺）
• その内部 $V$ から湧き出したり，吸い込まれたりする量（右辺）

次は，ストークスの定理 $$\oint_C \boldsymbol{A} \cdot d\boldsymbol{r} = \int_S \left(\nabla \times \boldsymbol{A}\right) \cdot \boldsymbol{n} dS$$ を証明します。ガウスの発散定理の証明と似ていますが，以下の4ステップで説明します。

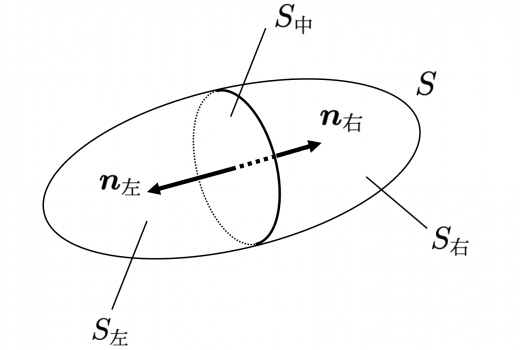
1. 任意のループの周回積分は分割して考えられる
2. 細かい四角形に分解し，
3. この四角形の一つに焦点をあてて周回積分を計算して，
4. それをたしあわせる

ループの周回積分は分割して考えられる

$\boldsymbol{A}$ の任意のループ $C$ に対する周回積分： $$\oint_C \boldsymbol{A} \cdot d\boldsymbol{r}$$ を考えます。

$C$ を，$C_{\text{中}}$ という線で，$C_{\text{左}}$ と $C_{\text{右}}$ という曲線に分割します。これら2つは図の矢印のような向きがある経路だと思ってください。また，$C_{\text{中}}$ にも向きをつけ，$C_{\text{左}} + C_{\text{中}\searrow}$ で一つのループ $C_1$，$C_{\text{右}} + C_{\text{中}\nwarrow}$ で一つのループ $C_2$ ができるようにします。

$C_1, C_2$ の周回積分について $$\begin{aligned} \oint_{C_1} \boldsymbol{A} \cdot d\boldsymbol{r} &= \int_{C_{\text{左}}} \boldsymbol{A} \cdot d\boldsymbol{r} + \int_{C_{\text{中}} \searrow} \boldsymbol{A} \cdot d\boldsymbol{r}\\ \oint_{C_2} \boldsymbol{A} \cdot d\boldsymbol{r} &= \int_{C_{\text{右}}} \boldsymbol{A} \cdot d\boldsymbol{r} + \int_{C_{\text{中}} \nwarrow} \boldsymbol{A} \cdot d\boldsymbol{r} \end{aligned}$$ です。$C_{\text{中}} \searrow, C_{\text{中}} \nwarrow$ は互いに逆向きの経路なので，これらの線積分の和は打ち消し合います。つまり， $$\int_{C_{\text{中}} \searrow} \boldsymbol{A} \cdot d\boldsymbol{r} + \int_{C_{\text{中}} \nwarrow} \boldsymbol{A} \cdot d\boldsymbol{r} = 0$$ が成立します。よって， $$\oint_{C_1} \boldsymbol{A} \cdot d\boldsymbol{r} + \oint_{C_2} \boldsymbol{A} \cdot d\boldsymbol{r} = \int_{C_{\text{左}}} \boldsymbol{A} \cdot d\boldsymbol{r} + \int_{C_{\text{右}}} \boldsymbol{A} \cdot d\boldsymbol{r} = \oint_C \boldsymbol{A} \cdot d\boldsymbol{r}$$ $$\therefore \oint_{C_1} \boldsymbol{A} \cdot d\boldsymbol{r} + \oint_{C_2} \boldsymbol{A} \cdot d\boldsymbol{r} = \oint_C \boldsymbol{A} \cdot d\boldsymbol{r} \tag{**}$$ この式 $(**)$ は，ガウスの発散定理の証明で登場した式 $(*)$ と同様に重要で，「任意のループ $C$ における $\boldsymbol{A}$ の周回積分は，それを分割したときにできる2つのループ $C_1, C_2$ における $\boldsymbol{A}$ の周回積分の和に等しい」ということを表しています。周回積分は面積分同様，好きなようにループを分割して良いわけです。

微小ループの集合として考える

$C$ を，$C$ とその中身が $C_1, C_2, \cdots, C_N$ という正方形型の微小ループで構成できるようになるまで切り刻んでいきます。

このとき，周回積分について， $$\oint_C \boldsymbol{A} \cdot d\boldsymbol{r} = \lim_{N \to \infty}\left\{\sum_{i = 1}^N \oint_{C_i} \boldsymbol{A} \cdot d\boldsymbol{r}\right\}$$ が成り立ちます。

任意のループの周回積分が微小ループの周回積分の総和で置き換えられました。

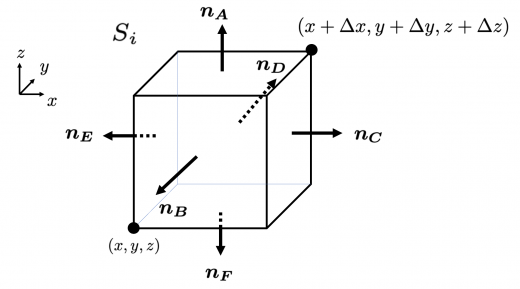
微小ループの周回積分を考える

まず，$xy$ 平面上に微小ループが乗っている場合を考えます。

この微小ループを $C_i$ と呼ぶことにします。このとき，$C_i$ の周回積分は $$\oint_{C} \boldsymbol{A} \cdot d\boldsymbol{r} = \int_{C_A} \boldsymbol{A} \cdot d\boldsymbol{r} + \int_{C_B} \boldsymbol{A} \cdot d\boldsymbol{r} + \int_{C_C} \boldsymbol{A} \cdot d\boldsymbol{r} + \int_{C_D} \boldsymbol{A} \cdot d\boldsymbol{r}$$ と計算できます。

ここで， $$\begin{aligned} \int_{C_A} \boldsymbol{A} \cdot d\boldsymbol{r} &= \int_x^{x + \Delta x} \left(\begin{array}{c} A_x\left(x,y,z\right)\\ A_y\left(x,y,z\right)\\ A_z\left(x,y,z\right) \end{array}\right) \cdot \left(\begin{array}{c} dx\\ 0\\ 0 \end{array}\right)\\ &= \left\{A_x\left(x,y,z\right) + \left(\Delta x \text{によるズレ}\right)\right\} \Delta x\\ &\approx A_x\left(x,y,z\right) \Delta x \end{aligned}$$ また， $$\begin{aligned} \int_{C_B} \boldsymbol{A} \cdot d\boldsymbol{r} &= \int_y^{y + \Delta y} \left(\begin{array}{c} A_x\left(x+\Delta x,y,z\right)\\ A_y\left(x+\Delta x,y,z\right)\\ A_z\left(x+\Delta x,y,z\right) \end{array}\right) \cdot \left(\begin{array}{c} 0\\ dy\\ 0 \end{array}\right)\\ &= \left\{A_y\left(x+\Delta x,y,z\right) + \left(\Delta y \text{によるズレ}\right)\right\} \Delta y\\ &\approx A_y\left(x+\Delta x,y,z\right) \Delta y \end{aligned}$$ 他についても同様に計算すれば $$\begin{aligned} \int_{C_C} \boldsymbol{A} \cdot d\boldsymbol{r} &= -A_x (x,y + \Delta y, z) \Delta x\\ \int_{C_D} \boldsymbol{A} \cdot d\boldsymbol{r} &= -A_y (x,y, z) \Delta y\\ \end{aligned}$$ これより， $$\begin{aligned} &\oint_{C_i} \boldsymbol{A} \cdot d\boldsymbol{r} \\&= \Delta x \left(A_x\left(x,y,z\right) -A_x (x,y + \Delta y, z)\right) + \Delta y \left(A_y\left(x+\Delta x,y,z\right)-A_y (x,y, z) \right)\\ &= \Delta x \left(-\dfrac{\partial{A_x}}{\partial{y}}\right)\Delta y + \Delta y \left(\dfrac{\partial{A_y}}{\partial{x}}\right)\Delta x\\ &= \Delta x \Delta y \left(\dfrac{\partial{A_y}}{\partial{x}} - \dfrac{\partial{A_x}}{\partial{y}}\right)\\ &= \Delta x \Delta y \left(\nabla \times \boldsymbol{A}\right)_z\\ &= \Delta x \Delta y \left(\nabla \times \boldsymbol{A}\right) \cdot \boldsymbol{n_z} \end{aligned}$$ 最後の行において，$\boldsymbol{n_z}$ は $+z$ 方向を向いている単位ベクトルです。

$yz$ 平面，$zx$ 平面にループが乗っている場合を同様に考えれば $$\begin{aligned} \oint_{C_i} \boldsymbol{A} \cdot d\boldsymbol{r} &= \Delta y \Delta z \left(\nabla \times \boldsymbol{A}\right) \cdot \boldsymbol{n_x}\\ \oint_{C_i} \boldsymbol{A} \cdot d\boldsymbol{r} &= \Delta z \Delta x \left(\nabla \times \boldsymbol{A}\right) \cdot \boldsymbol{n_y}\\ \end{aligned}$$

これらの式を見ると，$\displaystyle\oint_{C_i} \boldsymbol{A} \cdot d\boldsymbol{r}$ は $$(\text{ループの面積}) \cdot \left(\nabla \times \boldsymbol{A}\right) \cdot \boldsymbol{n_{\text{ループの単位法線ベクトル}}}$$ という形で記述できていることがわかります。同様に，任意の向きの微小ループに対して $$\oint_{C_i} \boldsymbol{A} \cdot d\boldsymbol{r} = \left(\nabla \times \boldsymbol{A}\right) \cdot \boldsymbol{n_i} \Delta S_i$$ と書くことができます。

もとの式に代入する

微小ループの結果を元の式に代入します。任意のループにおける周回積分は $$\oint_C \boldsymbol{A} \cdot d\boldsymbol{r} = \lim_{N \to \infty}\left\{\sum_{i = 1}^N \left(\nabla \times \boldsymbol{A}\right) \cdot \boldsymbol{n_i} \Delta S_i\right\}$$ 右辺を面積分で置き換えると， $$\oint_C \boldsymbol{A} \cdot d\boldsymbol{r} = \int_S \left(\nabla \times \boldsymbol{A}\right) \cdot \boldsymbol{n} dS$$ となり，証明が完了します。