ナビエ-ストークス方程式の導出

ナビエストークスと表記するのが面倒なので，以降NS方程式と呼ぶことにします。NS方程式： $$\rho \left\{\dfrac{\partial{\boldsymbol{v}}}{\partial{t}} + \left(\boldsymbol{v} \cdot \nabla \right) \boldsymbol{v}\right\} = -\nabla p + \mu \nabla^2 \boldsymbol{v} + \rho \boldsymbol{f}$$ において，$\rho$ は流体の密度，$\boldsymbol{v}(\boldsymbol{r},t)$ は流体の速度，$p(\boldsymbol{r},t)$ は流体にかかる圧力，$\mu$ は粘性係数，$\boldsymbol{f}$ は単位体積あたりに流体にかかる外力を表します。粘性係数 $\mu$ は簡単に言えば「物質の粘りの度合いを表す」ものであり，流体が持つ性質です。ある式の比例係数として登場します。

NS方程式には項に名前がついています。左辺第1項は時間微分項，左辺第2項は移流項（対流項），右辺第1項は圧力項，右辺第2項は粘性項，右辺第3項は外力項と呼ばれています。

NS方程式を運動方程式から導出するにあたり，流体の性質について非圧縮性を持ち，等質であるという仮定を設けようと思います。このような仮定を必要としないより一般的な流体を記述するNS方程式は他にもありますが，議論が入り組んでしまうので紹介しません。この記事で紹介するNS方程式でも，世の中のほとんどの流体の挙動を近似的に記述することができることが知られています。この意味でこのNS方程式は一般的なものです。

非圧縮性とは，「力を加えても縮んだり膨らんだりしない」という性質のことです。水をピストンで押すという実験を小学生や中学生のときにやった方も多いと思いますが，そのとき水はなかなか縮まなかったでしょう。世の中の流体はよほど大きな力を加えない限り，非圧縮性を満たすと近似して構わないことが実験的にわかっています。

また，等質であるとは，粘性係数 $\mu$ が至るところ一定であるという性質です。これも非圧縮性同様に，世の中の流体の多くが近似的にこの性質を満たします。

これらを仮定してNS方程式を導出することを考えてみます。

流体力学において重要となる物質微分（実質微分，ラグランジュ微分などとも呼ばれます）について説明します。

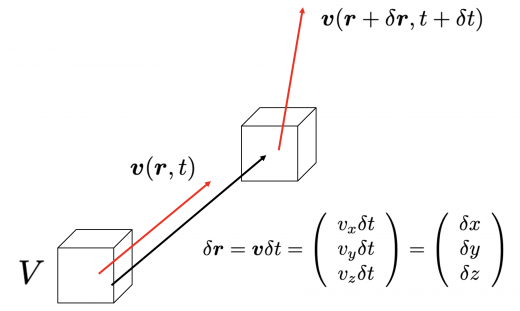
流体中の微小体積部分 $V$ に着目します。この物体の加速度は運動方程式により記述することができます。上図により，$V$ の加速度は以下のようにかけます。 $$\boldsymbol{a} \approx \dfrac{\delta \boldsymbol{v}}{\delta t} = \dfrac{\boldsymbol{v}(\boldsymbol{r} + \delta \boldsymbol{r}, t + \delta t) - \boldsymbol{v}(\boldsymbol{r},t)}{\delta t}$$ ここで，$\delta \boldsymbol{v} = \boldsymbol{v}(\boldsymbol{r} + \delta \boldsymbol{r}, t + \delta t) - \boldsymbol{v}(\boldsymbol{r},t)$ について，全微分の式より， $$\begin{aligned} \delta \boldsymbol{v} &= \dfrac{\partial{\boldsymbol{v}}}{\partial{t}}\delta t + \dfrac{\partial{\boldsymbol{v}}}{\partial{x}}\delta x + \dfrac{\partial{\boldsymbol{v}}}{\partial{y}}\delta y + \dfrac{\partial{\boldsymbol{v}}}{\partial{z}}\delta z\\ &= \dfrac{\partial{\boldsymbol{v}}}{\partial{t}}\delta t + \dfrac{\partial{\boldsymbol{v}}}{\partial{x}} v_x \delta t + \dfrac{\partial{\boldsymbol{v}}}{\partial{y}}v_y \delta t + \dfrac{\partial{\boldsymbol{v}}}{\partial{z}}v_z \delta t \end{aligned}$$ よって， $$\begin{aligned} \boldsymbol{a} &= \dfrac{\partial{\boldsymbol{v}}}{\partial{t}} + \dfrac{\partial{\boldsymbol{v}}}{\partial{x}} v_x + \dfrac{\partial{\boldsymbol{v}}}{\partial{y}}v_y + \dfrac{\partial{\boldsymbol{v}}}{\partial{z}}v_z\\ &= \dfrac{\partial{\boldsymbol{v}}}{\partial{t}} + (\boldsymbol{v} \cdot \nabla) \boldsymbol{v} \end{aligned}$$ となります。これにより，時間微分項，移流項がNS方程式に登場する理由が明らかになったと思います。

このように物体に沿って微分することを物質微分と言います。これを $$\dfrac{\mathrm{D}\boldsymbol{v}}{\mathrm{D}t} := \dfrac{\partial{\boldsymbol{v}}}{\partial{t}} + (\boldsymbol{v} \cdot \nabla) \boldsymbol{v}$$ と表記することが一般的です。スカラー場 $\phi(\boldsymbol{r}, t)$ に対しても，上記の $\boldsymbol{v}$ を $\phi$ に置き換えて同様に議論すれば， $$\dfrac{\mathrm{D}\phi}{\mathrm{D}t} := \dfrac{\partial{\phi}}{\partial{t}} + \boldsymbol{v}\cdot \nabla \phi$$ という式が自然に得られます。流体中のある部分に着目し，その部分における物理量を考える際にとても便利な考え方です。

空間内の任意の領域 $V$ を考えます。$V$ の内部にある流体の質量は，重積分を用いて $$\int_V \rho dV$$ で与えられます。ここから，$V$ 内の流体の単位時間あたりの質量の変化は $$\dfrac{\partial{}}{\partial{t}} \int_V \rho dV$$ によって与えられます。

一方，$V$ の表面を $S$ としたとき，$S$ から出ていく流体の質量は，面積分を用いて $$\int_S \rho\boldsymbol{v}\cdot \boldsymbol{n} dS$$ と表すことができます。ここで，ガウスの発散定理：

を用いれば， $$\int_S \rho\boldsymbol{v}\cdot \boldsymbol{n} dS = \int_V \nabla \cdot (\rho\boldsymbol{v}) dV$$ と表すことができます。

さて，流体が突然誕生したり消滅したりすることがない限り，$V$ 内の質量の変化は，表面 $S$ からの出入りのみに起因するはずです。よって， $$\begin{aligned} \dfrac{\partial{}}{\partial{t}} \int_V \rho dV &= - \int_V \nabla \cdot (\rho\boldsymbol{v}) dV\\ \therefore \int_V \left(\dfrac{\partial{\rho}}{\partial{t}} + \nabla \cdot (\rho\boldsymbol{v})\right) dV &= 0 \end{aligned}$$

$V$ は任意なので， $$\dfrac{\partial{\rho}}{\partial{t}} + \nabla \cdot (\rho\boldsymbol{v}) = 0 \tag{1}$$ 今，非圧縮性を仮定しているので，密度は変化しません。つまり，密度の物質微分は $0$ となるはずで， $$\dfrac{\mathrm{D}\rho}{\mathrm{D}t} := \dfrac{\partial{\rho}}{\partial{t}} + \boldsymbol{v}\cdot \nabla \rho = 0 \tag{2}$$ $(1),(2)$ により $$\nabla \cdot (\rho\boldsymbol{v}) = \boldsymbol{v}\cdot \nabla \rho$$ さて，ベクトル解析の公式により，

が成立すること（少しの計算により簡単に証明できます）を利用すると， $$\nabla \cdot (\rho\boldsymbol{v}) = (\nabla \rho) \cdot \boldsymbol{v} + \rho(\nabla \cdot \boldsymbol{v})$$ となるので， $$\rho(\nabla \cdot \boldsymbol{v}) = 0$$ が成立します。これにより $$\nabla \cdot \boldsymbol{v} = 0$$ を導けます。この式が非圧縮性から帰結されるもう一つの条件式です。あとでこれを用います。

$(x,y,z)$ を中心にもつ長さ $dx,dy,dz$ の微小直方体を考えます。

まずは $x$ 方向に働く圧力について考えます。$x$ 方向に働く圧力は以下の図のようになります。

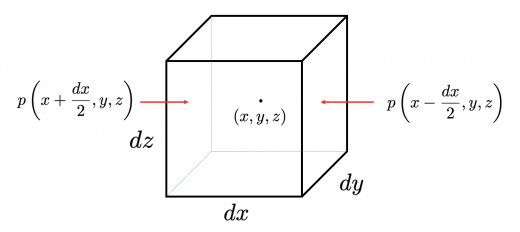
図より，$x$ 成分の合力は $$\begin{aligned} &\left\{p\left(x - \dfrac{dx}{2},y,z\right) - p\left(x + \dfrac{dx}{2},y,z\right)\right\}dydz\\ &\approx \left\{p(x,y,z) - \dfrac{dx}{2} \dfrac{\partial{p(x,y,z)}}{\partial{x}} - p(x,y,z) - \dfrac{dx}{2} \dfrac{\partial{p(x,y,z)}}{\partial{x}}\right\}dydz\\ &= -\dfrac{\partial{p(x,y,z)}}{\partial{x}} dxdydz \end{aligned}$$ ここで2行目の変形にはTaylor展開を用いています。これより，単位体積あたりの $x$ 成分の合力は $$-\dfrac{\partial{p(x,y,z)}}{\partial{x}}$$ となります。ここで，$y,z$ 成分についても同様に考えれば，単位体積あたりの $y,z$ 成分の合力は $-\dfrac{\partial{p(x,y,z)}}{\partial{y}}, -\dfrac{\partial{p(x,y,z)}}{\partial{z}}$ となりますから，圧力項はベクトルで表せば $$-\nabla p (x,y,z)$$ とできます。

流体には，接している面に対して，垂直な圧力のみではなく，接している面に対して平行な力も働きます。流体力学における「摩擦」です。流体力学ではこれを粘性応力と呼びます。また，垂直な方向（圧力と同じ方向）についても粘性応力は働きます。ドロドロした物体を持ち上げると，ある程度の量がくっついて一緒に持ち上がりますね。そのくっつきが垂直な方向の粘性応力です。

粘性応力は一般に $$\tau_{ij} = \mu \left(\dfrac{\partial{v_i}}{\partial{x_j}} + \dfrac{\partial{v_j}}{\partial{x_i}}\right) \tag{*}$$ と書くことができます。ここで $i,j$ は $1,2,3$ をとる変数であって，$1,2,3$ はそれぞれ $x,y,z$ に対応しています。応力は圧力と同様，単位面積あたりにかかる力であることに注意しましょう。

このように粘性応力がかけることは，ニュートンが実験的に見出した「ニュートンの粘性法則」に関連しています（より詳しく知りたい方はこの用語で検索してみると良いでしょう）。実験的に正しさが証明されているものとして受け入れてください。

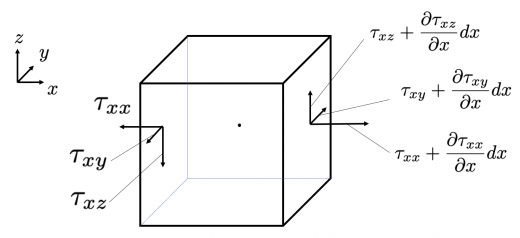
図より，$x$ 方向に働く粘性力の合力は， $$\dfrac{\partial{\tau_{xx}}}{\partial{x}} dx \cdot dydz + \dfrac{\partial{\tau_{yx}}}{\partial{y}} dy \cdot dxdz + \dfrac{\partial{\tau_{zx}}}{\partial{z}} dz \cdot dxdy = \left(\dfrac{\partial{\tau_{xx}}}{\partial{x}} + \dfrac{\partial{\tau_{yx}}}{\partial{y}} + \dfrac{\partial{\tau_{zx}}}{\partial{z}}\right)dxdydz$$ これより，単位体積あたりにかかる粘性力は $$\dfrac{\partial{\tau_{xx}}}{\partial{x}} + \dfrac{\partial{\tau_{yx}}}{\partial{y}} + \dfrac{\partial{\tau_{zx}}}{\partial{z}}$$ で表されます。式 $(*)$ を利用すれば $$\begin{aligned} &\mu \dfrac{\partial{}}{\partial{x}}\left(\dfrac{\partial{v_x}}{\partial{x}} + \dfrac{\partial{v_x}}{\partial{x}}\right) + \mu \dfrac{\partial{}}{\partial{y}}\left(\dfrac{\partial{v_y}}{\partial{x}} + \dfrac{\partial{v_x}}{\partial{y}}\right) + \mu \dfrac{\partial{}}{\partial{z}}\left(\dfrac{\partial{v_z}}{\partial{x}} + \dfrac{\partial{v_x}}{\partial{z}}\right)\\ &= \mu \left(\dfrac{\partial^2 v_x}{\partial x^2} + \dfrac{\partial^2 v_x}{\partial y^2} + \dfrac{\partial^2 v_x}{\partial z^2}\right) + \mu \dfrac{\partial{}}{\partial{x}}\left(\dfrac{\partial{v_x}}{\partial{x}} + \dfrac{\partial{v_y}}{\partial{y}} + \dfrac{\partial{v_z}}{\partial{z}}\right)\\ &= (\mu \nabla^2 \boldsymbol{v})_x + \mu \dfrac{\partial{}}{\partial{x}} \nabla \cdot \boldsymbol{v} \end{aligned}$$ ここで，節「非圧縮性から導かれるもう一つの条件式」で導いた式を用いれば $$(\mu \nabla^2 \boldsymbol{v})_x$$ が $x$ 方向の粘性項となります。$y,z$ 方向についても同様に考えれば $$\mu \nabla^2 \boldsymbol{v}$$ が粘性項となります。

外力項についてはあまり言うことはありません。NS方程式において外力項は流体同士が及ぼし合う力ではなく，遠くから作用するような力を指します。接しているがゆえに働くような力ではないということです。$\boldsymbol{f}$ は単位体積あたり，単位質量あたりに働く力を表します。例としては

• 重力
• コリオリ力
• 浮力
• 表面張力
• ローレンツ力

等が挙げられます。

これで全ての項が揃いました。「物質微分による時間微分項，移流項（対流項）の出現」で考えた微小体積部分 $V$ について運動方程式をたてます。この物体の体積を $\Delta V$ とすれば， $$\rho \Delta V \left(\dfrac{\partial{\boldsymbol{v}}}{\partial{t}} + (\boldsymbol{v} \cdot \nabla) \boldsymbol{v}\right) = \left(-\nabla p + \mu \nabla^2 \boldsymbol{v} + \rho \boldsymbol{f}\right) \Delta V$$ ここで $\Delta V$ を約分すればNS方程式を導くことができました。お疲れ様でした。

一般解は存在するのか？

NS方程式は現実に存在するたくさんの流体の挙動を予言する偉大な方程式です。もし，一般解を求めることができたら，流体の挙動は驚くほど簡単に予測することができるようになるでしょう。

しかし，NS方程式は解析的に解くには難しすぎるのです。NS方程式は「二階非線形偏微分方程式」と呼ばれる微分方程式です。$\nabla^2$ が入っていますから，「二階」であり，また移流項があるせいで「非線形」となっています。「非線形」である微分方程式は一般に解くことがとても難しいとされています。

このような事情から一般解は発見されていません。むしろ，一般解が存在するかどうかすらわかっていません。難しすぎるが故に，一般解を求めるか，一般解が存在しないことを証明できると，100万ドルがもらえる数学の重要な7つの問題「ミレニアム懸賞問題」として取り上げられています(→ミレニアム懸賞問題の概要と大雑把な説明)。