BSD予想の主張の解説

更新 2023/02/24

BSD予想 (バーチ・スウィンナートン＝ダイアー予想)

楕円曲線 $E$ の階数は， $E$ の $L$ 関数 $L(s, E)$ の $s=1$ における零点の位数に等しい。

ミレニアム懸賞問題とは，100万ドルの懸賞金がかけられている，数学における重要な7つの難問です。→ミレニアム懸賞問題の概要と大雑把な説明

このページでは，ミレニアム懸賞問題の1つであるBSD予想についてざっくりと説明します。特に楕円曲線について詳しく解説し， $L$ 関数については簡単に触れる程度とします。

楕円曲線とは

Q\mathbb{Q}Q 上で定義される楕円曲線というのは，a1,a2,⋯ ,a6∈Qa_{1}, a_{2}, \cdots , a_{6} \in \mathbb{Q}a1​,a2​,⋯,a6​∈Q に対して
y2+a1xy+a3y=x3+a2x2+a4x+a6
y^2 + a_{1}xy + a_{3}y = x^3 + a_{2}x^2 + a_{4}x + a_{6}
y2+a1​xy+a3​y=x3+a2​x2+a4​x+a6​
と表される曲線のことです。ただし，これは適切な変換により

y2=x3+ax+b(a,b∈Q)
y^2 = x^3 + ax + b \quad (a, b \in \mathbb{Q})
y2=x3+ax+b(a,b∈Q)

という形に帰着できることが知られています。
いくつかの楕円曲線について，具体的にその形を見てみましょう。
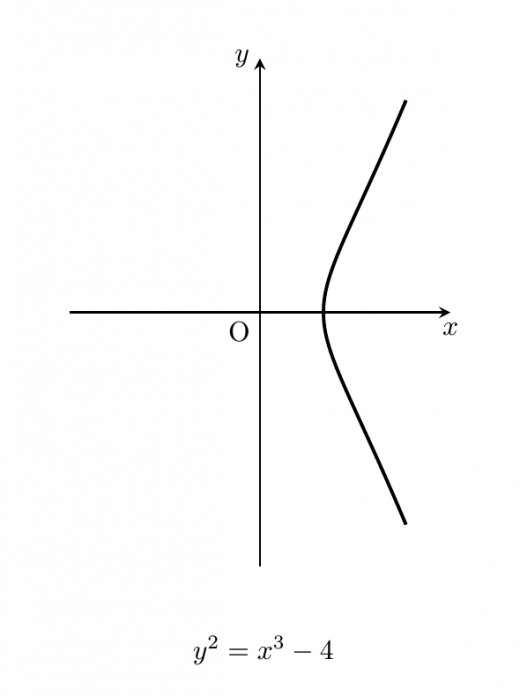
以下では，楕円曲線のうち退化しないもののみを考えます。その条件は，判別式 Δ=−16(4a3+27b2)\Delta = -16(4a^3+27b^2)Δ=−16(4a3+27b2) を用いて Δ≠0\Delta \neq 0Δ=0 と書くことができます。

楕円曲線上の有理点

楕円曲線 E:y2=x3+ax+bE: y^2 = x^3 + ax + bE:y2=x3+ax+b 上の有理点とは，点 (x,y)(x, y)(x,y) であって
y2=x3+ax+b，x,y∈Q
y^2 = x^3 + ax + b，\quad x, y \in \mathbb{Q}
y2=x3+ax+b，x,y∈Q
をみたすものを指します。EEE上の有理点全体の集合に無限遠点を加えたものを，
E(Q)E(\mathbb{Q})E(Q)とします。
いま，EEE 上の有理点 PPP，QQQ について，直線 PQPQPQ が EEE と再び点 RRR で交わるとします。このとき，解と係数の関係から，RRR は有理点であることがわかります。また，RRR と xxx 軸に関して対称な点をR′R'R′とすると，EEE は xxx 軸に関して線対称であることから R′R'R′ も EEE 上の有理点になることがわかります。
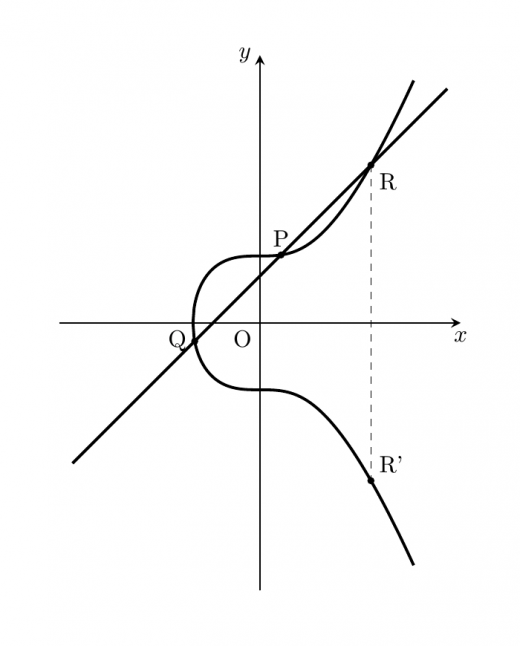
ここで，2点 PPP，QQQ から R′R'R′ を得ることを，演算 “+++” を用いて P+Q=R′P + Q = R'P+Q=R′ と表すこととします。このとき，E(Q)E(\mathbb{Q})E(Q) が無限遠点を単位元とするアーベル群となることが証明できます。
なお，群についてはこちらに説明があります。→群の定義といろいろな具体例

Mordellの定理

この $E(\mathbb{Q})$ に関して，以下の定理が知られています。

Mordell の定理

$E(\mathbb{Q})$ は有限生成なアーベル群である。すなわち，有限個の有理点 $P_{1}, P_{2}, \cdots, P_{n}$ が存在して， $E$ のすべての有理点は $P_{1}, P_{2}, \cdots , P_{n}$ から生成することができる。

アーベル群には階数という，次元を一般化したような値が定まります。特に，有限生成なアーベル群については，階数が有限であることが知られています。詳しくは, 有限生成アーベル群の基本定理について調べてみるとよいでしょう。

$E(\mathbb{Q})$ の階数のことを，楕円曲線 $E$ の階数と呼びます。すなわち，楕円曲線の階数は，無限個の有理点どうしの「多さ」を比べる指標と考えることができます。有理点が有限個の場合，階数は $0$ です。

有理点の「多さ」の指標となる階数の値を， $L(s, E)$ と表される関数のふるまいを調べることで決定できる，ということをBSD予想は主張しているのです。

L関数とは

最後に，LLL 関数とはなにか，位数とはなにかについて，簡単に触れておきます。以下，a，b∈Za，b \in \mathbb{Z}a，b∈Z とします。
まず，楕円曲線 E:y2=x3+ax+bE: y^2 = x^3 + ax + bE:y2=x3+ax+b について，
次の合同式をみたすような整数の組 (x,y)(x, y)(x,y) であって，0≦x<p0 \leqq x < p0≦x<p，0≦y<p0 \leqq y < p0≦y<p をみたすようなものの個数を Np(E)N_{p}(E)Np​(E) とします。
y2≡x3+ax+b(mod p)
y^2 \equiv x^3 + ax + b \quad (\mathrm{mod}\:p)
y2≡x3+ax+b(modp)
また，ap(E)=p−Np(E)a_p(E) = p - N_p(E)ap​(E)=p−Np​(E) とします。
このとき，Δ=−16(4a3+27b2)\Delta = -16(4a^3+27b^2)Δ=−16(4a3+27b2) を割り切る素数 ppp が存在しないならば，EEE の LLL 関数は

L(s,E)=∏p:素数11−ap(E)p−s+p1−2s
L(s, E) = \prod_{p: 素数} \frac{1}{1 - a_p(E) p^{-s} + p^{1-2s}}
L(s,E)=p:素数∏​1−ap​(E)p−s+p1−2s1​

と表されます。
ただし，Δ\DeltaΔ を割り切る素数 ppp が存在する場合は，その ppp についての項のみ修正が必要です。
この LLL 関数は，複素数の範囲に定義域を広げられる(=解析接続される)ことが知られています。
解析接続についてはこちらでも触れられています。→ゼータ関数の定義と基本的な話
また，LLL 関数が L(1,E)=0L(1, E) = 0L(1,E)=0 をみたし，そのテイラー展開が
L(s,E)=ak(E)(s−1)k+ak+1(E)(s−1)k+1+⋯
L(s, E) = a_{k}(E)(s-1)^{k} + a_{k+1}(E)(s-1)^{k+1} + \cdots
L(s,E)=ak​(E)(s−1)k+ak+1​(E)(s−1)k+1+⋯
と書けるとき，この kkk の値を LLL の s=1s=1s=1 における零点の位数と呼びます。
L(1,E)≠0L(1, E) \neq 0L(1,E)=0 のときは，s=1s=1s=1 における零点の位数は 000 となります。したがって，BSD予想が正しいならば，このときの EEE の階数は 000 ，すなわち有理点は有限個であるとわかります。
解析接続や位数については詳しく述べると長くなってしまうので，興味のある方は複素解析の教科書を参照してください。

余談

$L$ 関数は，実はゼータ関数と非常に類似した関数です。詳しくは，ゼータ関数のオイラー積表示について調べてみるとよいでしょう。

また，楕円曲線上の有理点の加算は，楕円曲線暗号(ECC)と呼ばれる暗号にも使用されています。2点 $P$ ， $Q$ について， $P$ をいくつ加算すれば $Q$ を得られるかを求める問題は楕円曲線上の離散対数問題と呼ばれており，この困難性をもとに，暗号として利用されているそうです。

楕円曲線～フェルマーの最終定理・BSD予想・合同数問題と合わせてもご覧ください。

楕円曲線は，フェルマーの最終定理の証明にも登場します。しかし，それについて詳しく述べるには，この余白は小さすぎますね。