リサージュ曲線の定義とそれに関連する話

更新 2023/05/27

媒介変数 $\theta$ を用いて， $\begin{cases} x = A\sin (a\theta + \delta)\\ y = B\sin (b\theta) \end{cases}$ と表される曲線をリサージュ曲線という。

リサージュ曲線の定義と関連する話題を紹介します。

リサージュ曲線の定義

リサージュ曲線，またはリサージュ図形とは，2つの単振動を合成して得られる平面上の図形のことです。振れ幅 A,BA,BA,B，振動数 a,ba,ba,b，位相差 δ\deltaδ 
によって様々な図形を得られます。


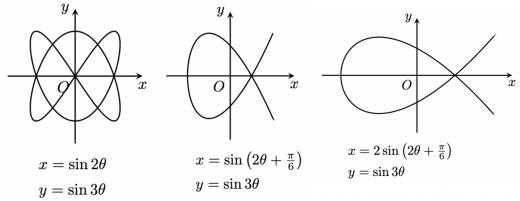
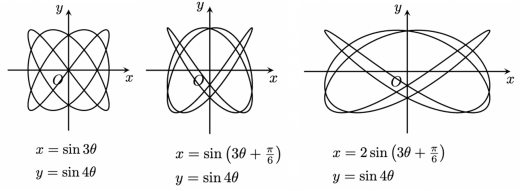
リサージュ曲線は，フランスの物理学者 Jules Antoine Lissajous が考案したものです。日本語での表記は揺れており「リサジュー曲線」と呼ばれることもあります。
オシロスコープのような役割をするもの（今はコンピュータを使えば良いですね）を用意して波形を描いてみると，とても楽しいです。

リサージュ曲線の概形を手計算で描いてみる

コンピュータを使わずに，手計算でも概形を描けます。例題として以下のリサージュ曲線を考えてみます。
リサージュ曲線の例
{x(θ)=3sin⁡θy(θ)=2sin⁡(2θ+π6)
\begin{cases}
x(\theta) = 3 \sin \theta\\
y(\theta) = 2 \sin \left(2\theta + \dfrac{\pi}{6}\right)
\end{cases}
{x(θ)=3sinθy(θ)=2sin(2θ+6π​)​
と表されるリサージュ曲線の概形を描け。
まず最初に対称性がないかを確認します。θ→π+θ\theta \to \pi + \thetaθ→π+θ とした時に，
x(π+θ)=−3sin⁡θ=−x(θ)
x(\pi + \theta) = -3\sin\theta = -x(\theta)
x(π+θ)=−3sinθ=−x(θ)
また，
y(π+θ)=2sin⁡(2π+2θ+π6)=2sin⁡(2θ+π6)=y(θ)\begin{aligned}
y(\pi + \theta) &= 2\sin\left(2\pi + 2\theta + \dfrac{\pi}{6}\right) \\
&= 2\sin\left( 2\theta + \dfrac{\pi}{6}\right) = y(\theta)
\end{aligned}y(π+θ)​=2sin(2π+2θ+6π​)=2sin(2θ+6π​)=y(θ)​
となります。よって，0≦θ≦π0 \leqq \theta \leqq \pi0≦θ≦π の間で概形を描いて，それを xxx 軸に関して対称移動させれば良いです。これらを微分すると，
{dxdθ=3cos⁡θdydθ=4cos⁡(2θ+π6)
\begin{cases}
\dfrac{dx}{d\theta} = 3\cos \theta\\
\dfrac{dy}{d\theta} = 4\cos \left( 2\theta + \dfrac{\pi}{6}\right)
\end{cases}
⎩⎨⎧​dθdx​=3cosθdθdy​=4cos(2θ+6π​)​
により，増減表は以下のようになります。
θ0⋯π6⋯π2⋯23π⋯πdxdθ++++0−−−−dydθ++0−−−0++(x,y)(0,1)↗(32,2)↘(3,−1)↙(332,−2)↖(0,1)
\begin{array}{c|ccccccc}
  \theta  &0& \cdots & \dfrac{\pi}{6}& \cdots &\dfrac{\pi}{2}& \cdots &\dfrac{2}{3}\pi & \cdots &\pi\\ 
  \hline
  \dfrac{dx}{d\theta} & + & + & + & + & 0 & -& -& -& -
\\ 
  \hline
  \dfrac{dy}{d\theta} & + & + & 0 & - & - & -& 0& +& +
\\ 
  \hline
  (x,y)  & (0,1) & \nearrow & \left(\dfrac{3}{2}, 2\right) & \searrow & (3,-1)& \swarrow & \left(\dfrac{3\sqrt{3}}{2},-2\right) & \nwarrow & (0,1)
\end{array}
θdθdx​dθdy​(x,y)​0++(0,1)​⋯++↗​6π​+0(23​,2)​⋯+−↘​2π​0−(3,−1)​⋯−−↙​32​π−0(233​​,−2)​⋯−+↖​π−+(0,1)​​
よって，0≦θ≦2π0 \leqq \theta \leqq 2\pi0≦θ≦2π の範囲で概形を描くと以下の通りになります。
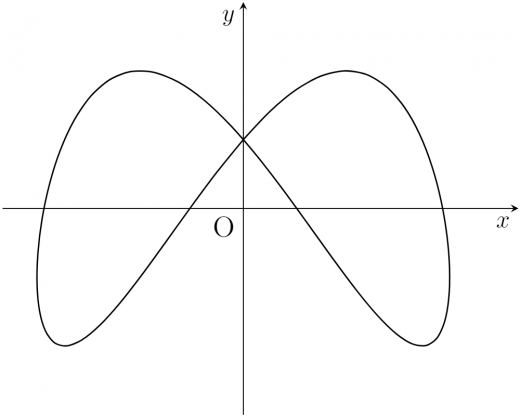
どこで極大・極小になるのか詳しく書くと次のようになります。

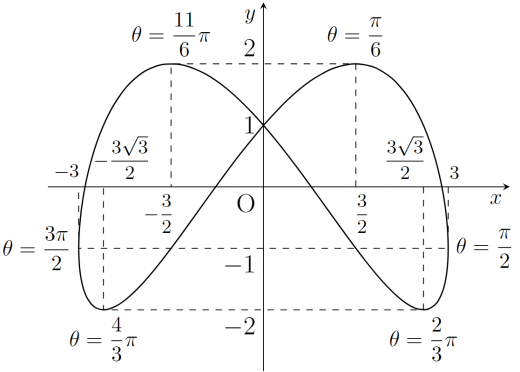
リサージュ曲線で囲まれた領域の面積

練習問題

$\begin{cases} x(\theta) = 3 \sin \theta\\ y(\theta) = 2 \sin \left(2\theta + \dfrac{\pi}{6}\right) \end{cases}$ と表されるリサージュ曲線で囲まれた領域の面積を求めよ。

数Ⅲ積分の練習問題です。

証明

$x \geqq 0$ の部分の面積を計算して2倍すればよい。 $x \geqq 0$ の部分の面積を $S$ とおく。

$S = \int_{-2}^{2} x dy - \int_1^2 x dy - \int_{-2}^1 x dy$ である。

$\theta$ に変数を置き換える。 $\begin{aligned} dy &= 4 \cos \left( 2\theta + \dfrac{\pi}{6} \right) d\theta\\ &= (2\sqrt{3} \cos 2\theta - 2\sin 2\theta) d\theta \end{aligned}$ であるため，被積分関数は $\begin{aligned} xdy &= 3\sin \theta (2\sqrt{3} \cos 2\theta - 2\sin 2\theta) d\theta\\ &= 6 (\sqrt{3} \sin \theta \cos 2\theta - \sin \theta \sin 2\theta) d\theta\\ &= 3 (\sqrt{3} \sin 3\theta - \sqrt{3} \sin \theta + \cos 3\theta - \cos \theta) d\theta \end{aligned}$ となる。

1項目 $\begin{aligned} &\int_{-2}^2 xdy\\ &= \int_{\frac{2}{3} \pi}^{\frac{\pi}{6}} 3 (\sqrt{3} \sin 3\theta - \sqrt{3} \sin \theta + \cos 3\theta - \cos \theta) d\theta\\ &= -3\Big[ -\dfrac{\sqrt{3}}{3} \cos 3\theta + \sqrt{3} \cos \theta + \dfrac{1}{3} \sin 3\theta - \sin \theta \Big]_{\frac{\pi}{6}}^{\frac{2}{3} \pi}\\ &= 4+4\sqrt{3} \end{aligned}$
2項目

$\begin{aligned} &\int_1^2 xdy\\ &= \int_{0}^{\frac{\pi}{6}} 3 (\sqrt{3} \sin 3\theta - \sqrt{3} \sin \theta + \cos 3\theta - \cos \theta) d\theta\\ &= 3\Big[ -\dfrac{\sqrt{3}}{3} \cos 3\theta + \sqrt{3} \cos \theta + \dfrac{1}{3} \sin 3\theta - \sin \theta \Big]_0^{\frac{\pi}{6}}\\ &= 2-2\sqrt{3} \end{aligned}$

3項目

$\begin{aligned} &\int_{-2}^1 xdy\\ &= \int_{\frac{2}{3} \pi}^{\pi} 3 (\sqrt{3} \sin 3\theta - \sqrt{3} \sin \theta + \cos 3\theta - \cos \theta) d\theta\\ &= 3\Big[ -\dfrac{\sqrt{3}}{3} \cos 3\theta + \sqrt{3} \cos \theta + \dfrac{1}{3} \sin 3\theta - \sin \theta \Big]_{\frac{2}{3} \pi}^{\pi}\\ &= 2\sqrt{3} \end{aligned}$

以上より $\begin{aligned} S &= (4+4\sqrt{3}) - (2-2\sqrt{3}) - 2\sqrt{3}\\ &= 4\sqrt{3} + 2 \end{aligned}$ であるため，求める面積は $\mathbf{8\sqrt{3}+4}$ である。

振動数の比が有理数だと閉曲線になる

リサージュ曲線に関する簡単な定理を紹介します。
定理
リサージュ曲線
{x=Asin⁡(aθ+δ)y=Bsin⁡(bθ)
\begin{cases}
x = A\sin (a\theta + \delta)\\
y = B\sin (b\theta)
\end{cases}
{x=Asin(aθ+δ)y=Bsin(bθ)​
において，振動数の比 ba\dfrac{b}{a}ab​ が有理数のとき，リサージュ曲線はどこかのタイミングで開始点に戻ってくる閉曲線になる。
これが正しいことを説明します。
xxx の周期は 2πa\dfrac{2\pi}{a}a2π​ で，yyy の周期は 2πb\dfrac{2\pi}{b}b2π​ です。よって「2πa\dfrac{2\pi}{a}a2π​ の整数倍」かつ「2πb\dfrac{2\pi}{b}b2π​ の整数倍」となる実数 TTT があれば時刻 TTT で開始点に戻ってきます。
そこで，2πa×M=2πb×N\dfrac{2\pi}{a} \times M = \dfrac{2\pi}{b} \times Na2π​×M=b2π​×N
つまり
ba=NM\dfrac{b}{a} = \dfrac{N}{M}ab​=MN​
となる整数 M,NM,NM,N が存在することを示せばよいです。実際，このような M,NM,NM,N は ba\dfrac{b}{a}ab​ が有理数なので存在します。
例えば，前節の
{x(θ)=3sin⁡θy(θ)=2sin⁡(2θ+π6)
\begin{cases}
x(\theta) = 3 \sin \theta\\
y(\theta) = 2 \sin \left(2\theta + \dfrac{\pi}{6}\right)
\end{cases}
{x(θ)=3sinθy(θ)=2sin(2θ+6π​)​
において，振動数の比は 12\dfrac{1}{2}21​ であるので，xxx が 111 回振動し，yyy が 222 回振動すると，開始点に戻ってきます。
また，
{x(θ)=5sin⁡4θy(θ)=6sin⁡(12θ+π3)
\begin{cases}
x(\theta) = 5 \sin 4\theta\\
y(\theta) = 6 \sin \left(12\theta + \dfrac{\pi}{3}\right)
\end{cases}
{x(θ)=5sin4θy(θ)=6sin(12θ+3π​)​
において，振動数の比は 412=13\dfrac{4}{12} = \dfrac{1}{3}124​=31​ であるから，xxx が 111 回振動し，yyy が 333 回振動すると，開始点に戻ってきます。このように振動数どうしが公約数を持っているほど，開始点に戻ってくるのは早くなります。 概形は以下のようになります。
よって例えば，
{x(θ)=2sin⁡10θy(θ)=3sin⁡11θ
\begin{cases}
x(\theta) = 2 \sin 10\theta\\
y(\theta) = 3 \sin 11\theta 
\end{cases}
{x(θ)=2sin10θy(θ)=3sin11θ​
を考えると，振動数の比は 1011\dfrac{10}{11}1110​ であるから，xxx が 101010 回振動し，yyy が 111111 回振動しなければ，閉曲線になりません。点は長い時間新しい場所を振動します。概形は以下のようになります。

振動数の比が無理数だと閉曲線にならない

では振動数の比が無理数の場合どうなるでしょうか。有理数の場合に分子分母が大きいほど図形がなかなか閉じなかったことから考えると，点は新しいところだけを永遠に通り続けて，閉曲線にはならないんじゃないか？と予測されます。

定理

リサージュ曲線 $\begin{cases} x = A\sin (a\theta + \delta)\\ y = B\sin (b\theta) \end{cases}$ において，振動数の比 $\dfrac{b}{a}$ が無理数のとき，リサージュ曲線は閉曲線にならない。

これも有理数のときと同様な議論で説明できます。

$x,y$ の周期はそれぞれ $\dfrac{2\pi}{a}, \dfrac{2\pi}{b}$ である。もしこの曲線が閉曲線であれば，整数 $M,N$ が存在して， $x$ が $M$ 回振動し，また $y$ が $N$ 回振動したときに開始点に戻ってきたという状況がある。このとき， $\dfrac{2\pi}{a} \times M = \dfrac{2\pi}{b} \times N\\ \therefore \dfrac{b}{a} = \dfrac{N}{M}$ $\dfrac{b}{a}$ は無理数であるのに対し， $\dfrac{M}{N}$ は有理数であるからこれは矛盾。よって，このリサージュ曲線は閉曲線にならない。

閉曲線にならないということは， $\theta$ が増えるにつれて，点は今まで通ったことのない領域を通り続けます。また， $x$ は常に $-A \leqq x \leqq A$ , $y$ は常に $-B \leqq y \leqq B$ を動き続けます。よって無限に $\theta$ を大きくしていけば，縦 $2A$ , 横 $2B$ の平行四辺形を塗りつぶすように点が動くと予想されます。このことについての一般的な証明は難しいので話題にあげる程度に留めておきますが，例をみてみると面白いです。

リサージュ曲線 $\begin{cases} x(\theta) = 2 \sin \left(\theta + \dfrac{\pi}{4}\right)\\ y(\theta) = \sin \left(\sqrt{2}\theta + \dfrac{\pi}{6}\right) \end{cases}$ を例にとって， $\theta$ を $0$ から動かしていくと，以下のようになります。

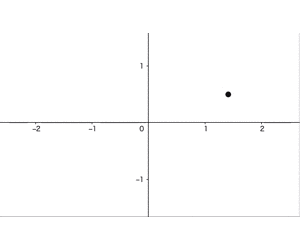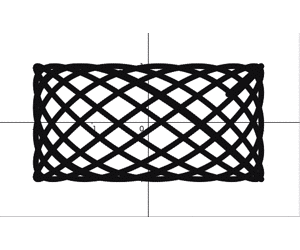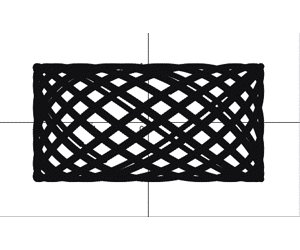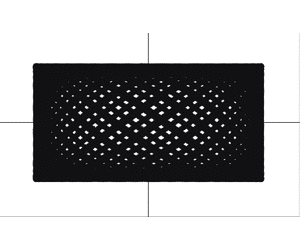
振動数の比ルート2のリサージュ曲線

現実世界で現れるリサージュ曲線

現実世界でリサージュ曲線が現れる例をみてみましょう。以下のような構造の振り子を考えてみます。
上の二点は空間内に固定しています。糸は常にピンと貼ってある状態です。振り子は振れ幅が大きくない時には，単振動の運動，つまり三角関数を使って位置を表現できる運動に近似できます。
この状況で振り子を横に振動させると，以下のような運動をします。
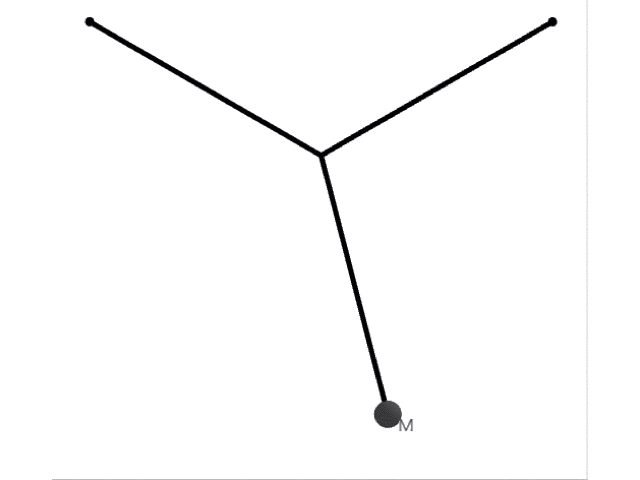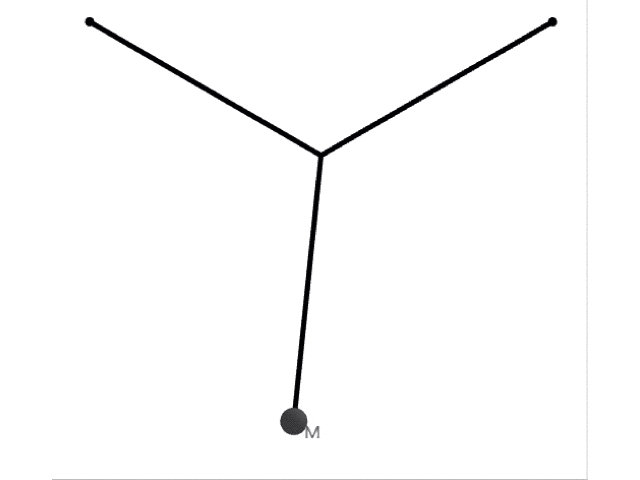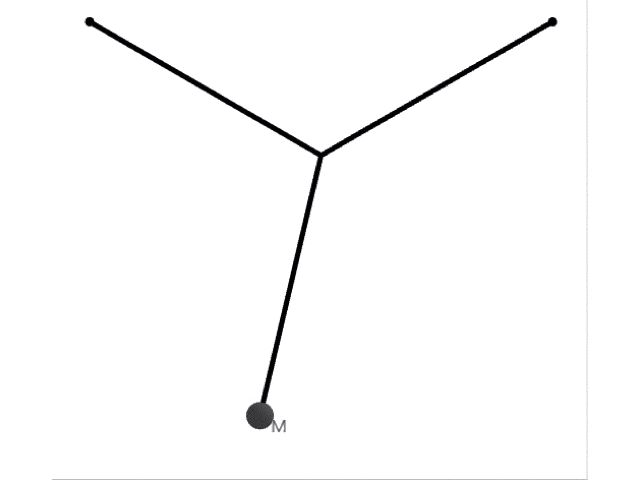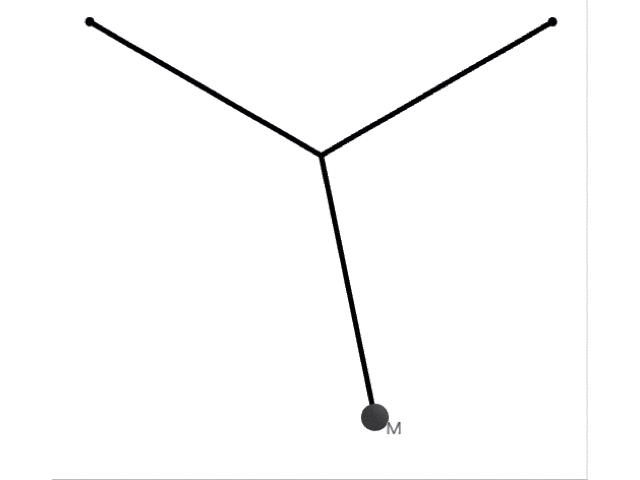
つまり，横には長さが L1L_1L1​ の振動をします。上の2本の糸は振動に関与しません。よって周期は，物理で習う公式を利用すれば，重力加速度 ggg を使って 2πL1g2\pi \sqrt{\dfrac{L_1}{g}}2πgL1​​​ と表せます。
これに対し，画面に対して垂直な方向（以降「縦」方向と呼びます）に振り子を振動させると，以下のような運動をします。
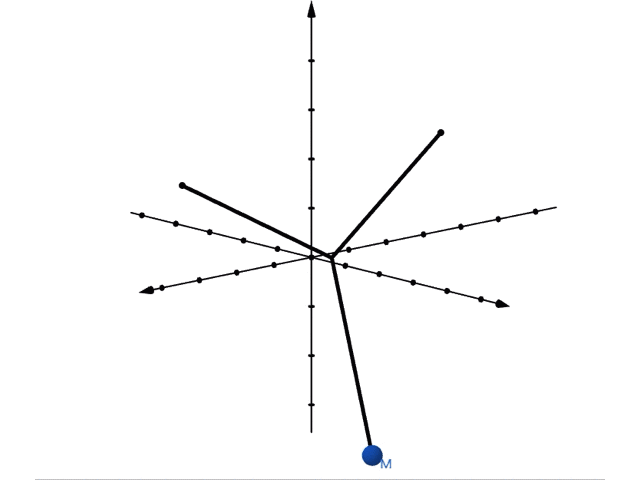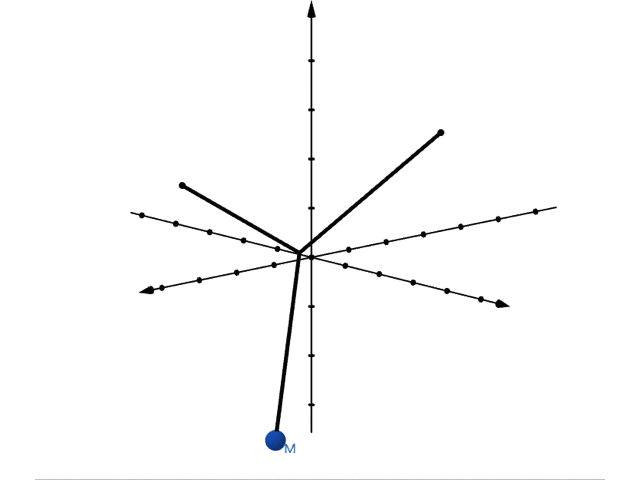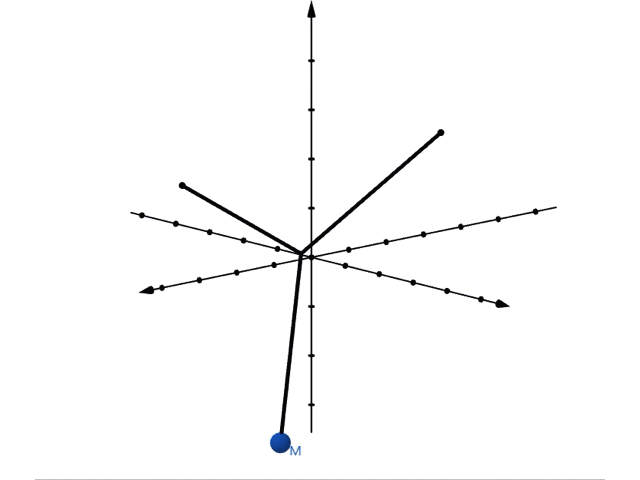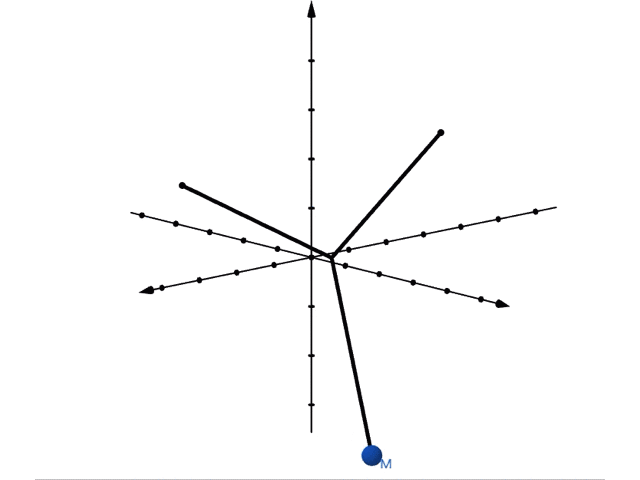
縦には長さが L2L_2L2​ の振動します。周期は，2πL2g2\pi \sqrt{\dfrac{L_2}{g}}2πgL2​​​ になります。
L1,L2L_1,L_2L1​,L2​ の長さは違うので，周期も異なります。一般には横と縦の振動の重ね合わせの運動をするはずですので，まさしくこれはリサージュ曲線を描きます。
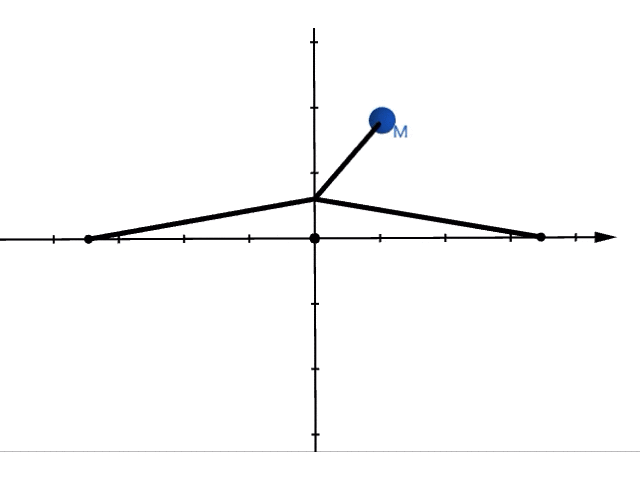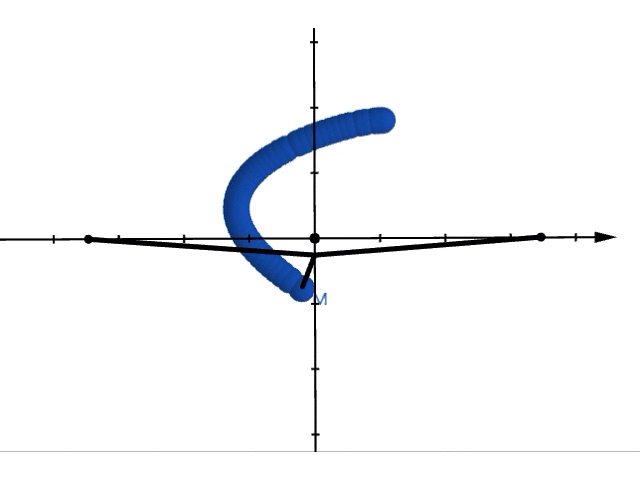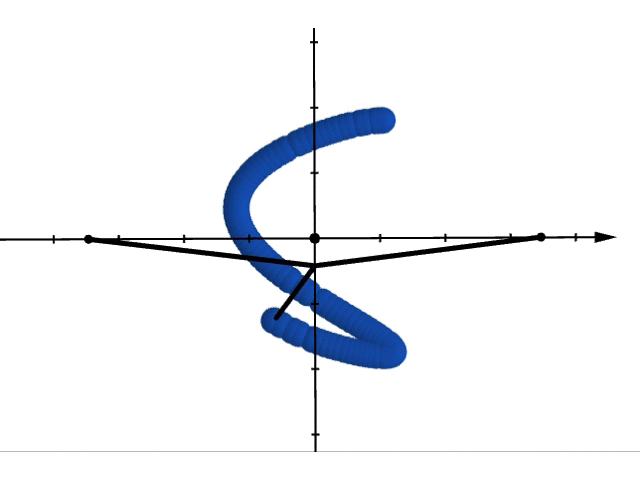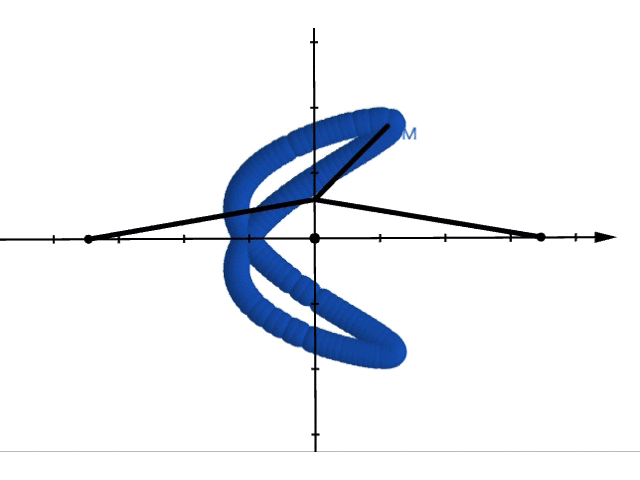
では実際に重ね合わせた運動をみてみましょう。位置が，
{x=35cos⁡(2θ+π6)y=910cos⁡θ
\begin{cases}
x = \dfrac{3}{5} \cos\left(2\theta + \dfrac{\pi}{6}\right)\\
y = \dfrac{9}{10} \cos\theta\\
\end{cases}
⎩⎨⎧​x=53​cos(2θ+6π​)y=109​cosθ​
で表されるような振り子の運動は以下のようになります。
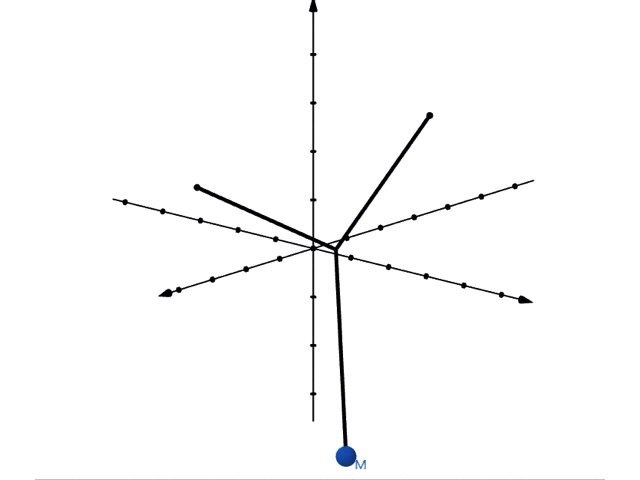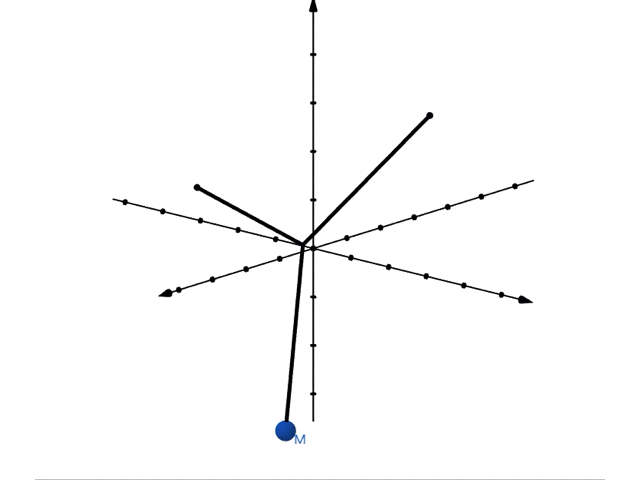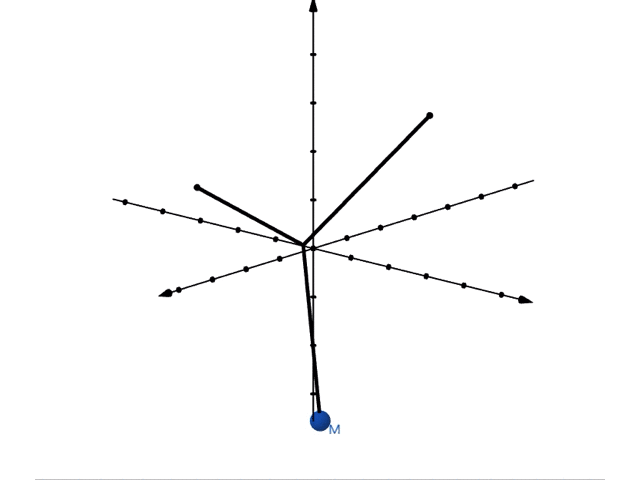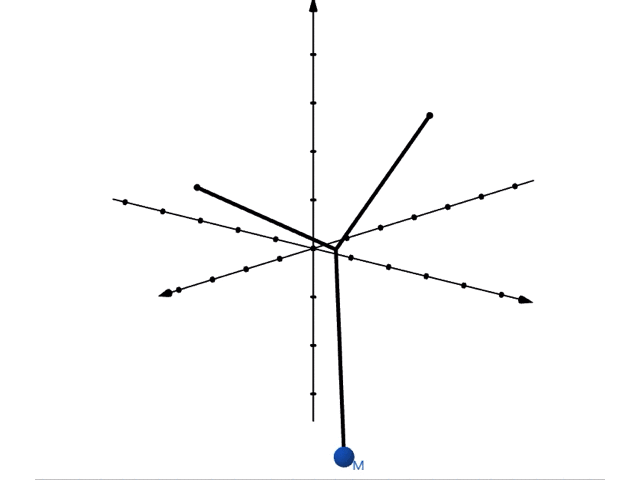
これを上から眺めてみると，リサージュ曲線ができることがわかります。

3次元空間におけるリサージュ曲線

3次元においても，媒介変数表示を使ってリサージュ曲線を同様に表せます。例えば， $\begin{cases} x = 2\sin \left(2\theta + \dfrac{\pi}{6}\right)\\ y = 3\sin (4\theta)\\ z = 4\sin \left(3\theta + \dfrac{\pi}{4}\right)\\ \end{cases}$ は，空間上で次のような図形になります。 3次元のリサージュ曲線

また，2次元の時と同様に， $\begin{cases} x = 2\sin \left(2\theta\right)\\ y = 3\sin (\sqrt{2}\theta)\\ z = 4\sin \left(\sqrt{3}\theta\right)\\ \end{cases}$ で表されるリサージュ曲線は，振動数の比が無理数であるから，直方体のような形の立体図形になります。

三角関数という単純な式を使うだけで，このような美しい模様がかけるのがとても楽しいですね。

この記事の監修者

でーちー

公立地方進学校出身。高校時代は部活動に勤しみ，合間を縫って勉強を進めた。受験生時代には毎日12時間以上の勉強を続け，東京大学理科一類に現役合格。大学でも数学・物理を得意とし，情報系の学科に進みつつも，独学で勉強を続けている。学びTimesでは主に「高校数学の美しい物語」「高校生から味わう理論物理入門」の記事執筆・修正業務に尽力している。