楕円曲線～フェルマーの最終定理・BSD予想・合同数問題と合わせて

楕円曲線と概形

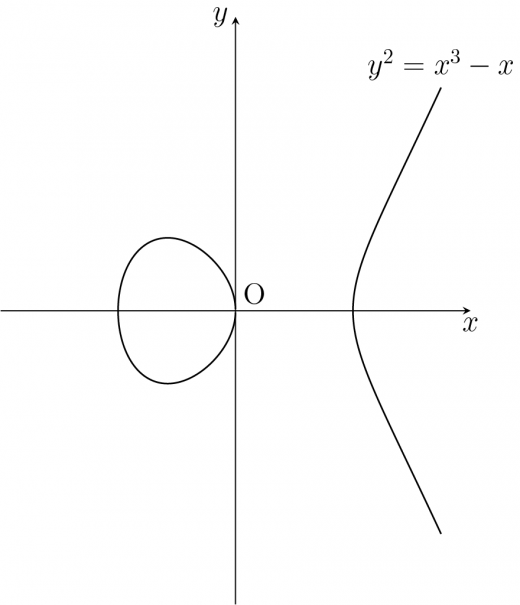
楕円曲線はひょうたんのような形になることが多いです。例を見てみましょう。
次のように「離島」がある曲線もあります。
ワイエルシュトラスの標準形楕円曲線の右辺にはなぜ x2x^2x2 の項が無いのでしょうか？
実は，y2=x3+px2+qx+ry^2 = x^3 + px^2 + qx + ry2=x3+px2+qx+r のことを楕円曲線と呼ぶこともありますが，x→X−p3x \to X -\dfrac{p}{3}x→X−3p​ と変換することで，x2x^2x2 の項を消去できます。
y2=x3+ax+by^2 = x^3 + ax + by2=x3+ax+b のように x2x^2x2 の項がない表記をワイエルシュトラスの標準形といいます。
ワイエルシュトラスの標準形で考えると，後述の「群構造」のパートの証明が簡単になります。
また，y2=p′x3+q′x+r′y^2 = p' x^3 + q' x + r'y2=p′x3+q′x+r′ と表されるとき，(x,y)(x,y)(x,y) を (p′x,p′2y)(p' x,p'^2 y)(p′x,p′2y) に取り換えることで，x3x^3x3 の係数を 111 にすることができます。以上をまとめると，楕円曲線とは y2=(xの3次式)y^2 = (x \text{の3次式})y2=(xの3次式) で表される曲線であると定義できます。

楕円曲線と群構造

楕円曲線 EEE に「(yyy 軸方向の)無限遠点」を追加した集合には群の構造が入ります。
無限遠点「(yyy 軸方向の)無限遠点」なるものを考えます。
この記事では「(yyy 軸方向の)無限遠点」を ∞\infty∞ と表記します。
「yyy 軸と平行な直線は ∞\infty∞ を通る」と考えます。
また「EEE も ∞\infty∞ を通る」と考えます。楕円曲線の式で xxx を限りなく大きくすると ∣y∣|y|∣y∣ も限りなく大きくなるからです。
無限遠点については，射影平面の３通りの定義 も参考にしてください。
加法の定義E~\tilde{E}E~ で E∪{∞}E \cup \{ \infty \}E∪{∞} を表すことにします。
定理
E~\tilde{E}E~ 上の2点 P\mathrm{P}P，Q\mathrm{Q}Q について，P⊕Q\mathrm{P} \oplus \mathrm{Q}P⊕Q を以下で定義する。
E~\tilde{E}E~ と直線 PQ\mathrm{PQ}PQ の（重複を含めた）交点のうち P\mathrm{P}P，Q\mathrm{Q}Q ではない点を R\mathrm{R}R とする。
R\mathrm{R}R と xxx 軸に関して対称な点を P⊕Q\mathrm{P} \oplus \mathrm{Q}P⊕Q とする。
このとき E~\tilde{E}E~ は ⊕\oplus⊕ を演算とする可換群となる。
定義だけではわかりにくいので，いろいろな P\mathrm{P}P と Q\mathrm{Q}Q に対して P⊕Q\mathrm{P} \oplus \mathrm{Q}P⊕Q を計算してみましょう。
P，Q が EEE 上にあるときEEE 上の点 P(x1,y1)\mathrm{P} (x_1 , y_1)P(x1​,y1​)，Q(x2,y2)\mathrm{Q} (x_2 , y_2)Q(x2​,y2​) を取ります。
x1≠x2x_1 \neq x_2x1​=x2​ のとき計算
直線 PQ\mathrm{PQ}PQ の式を y=mx+ny = mx + ny=mx+n とおく。（m=y2−y1x2−x1m = \dfrac{y_2 - y_1}{x_2 - x_1}m=x2​−x1​y2​−y1​​ である。）
このとき PQ\mathrm{PQ}PQ と EEE の交点の xxx 座標は3次方程式
x3+ax+b=(mx+n)2
x^3 + ax + b = (mx+n)^2
x3+ax+b=(mx+n)2
の実数解である。既に実数 x=x1,x2x = x_1 , x_2x=x1​,x2​ が解である。3次方程式の実数解は1つか3つであるので，上の方程式の解は3つである。
上の計算によって，EEE 上に3つ目の交点 R(x3,y3)\mathrm{R} (x_3 , y_3)R(x3​,y3​) を取れます。
P⊕Q=(x3,−y3)\mathrm{P} \oplus \mathrm{Q} = (x_3 , -y_3)P⊕Q=(x3​,−y3​) です。
x1=x2x_1 = x_2x1​=x2​，y1≠y2y_1 \neq y_2y1​=y2​ のときこのとき直線 PQ\mathrm{PQ}PQ は yyy 軸と平行な直線 x=x1x = x_1x=x1​ となります。この直線は EEE とは2点でしか交わりませんが，無限遠点を通ります。よって E~\tilde{E}E~ と3点で交わります。
ゆえにこのとき P⊕Q=∞\mathrm{P} \oplus \mathrm{Q} = \inftyP⊕Q=∞ となります。
x1=x2x_1 = x_2x1​=x2​，y1=y2y_1 = y_2y1​=y2​ のときP\mathrm{P}P と Q\mathrm{Q}Q が一致するときは，直線 PQ\mathrm{PQ}PQ は P\mathrm{P}P での接線と考えます。
Q が無限遠点であるとき無限遠点 ∞\infty∞ は単位元になる。
以下で，P⊕∞=P\mathrm{P} \oplus \infty=\mathrm{P}P⊕∞=P であることを確認してみましょう。
P が EEE 上にあるときP(x1,y1)\mathrm{P} (x_1 , y_1)P(x1​,y1​) と無限遠点を通る直線は x=x1x = x_1x=x1​ です。このとき E~\tilde{E}E~ と (x1,−y1)(x_1 , -y_1)(x1​,−y1​) で交わります。
つまり P⊕∞=(x1,y1)=P\mathrm{P} \oplus \infty = (x_1 , y_1) = \mathrm{P}P⊕∞=(x1​,y1​)=P です。
P も無限遠点であるとき考え方は省略しますが，∞⊕∞=∞\infty \oplus \infty = \infty∞⊕∞=∞ となります。
結合法則についてE~\tilde{E}E~ 上の加法 ⊕\oplus⊕ について結合律が成立します。
すなわち (P⊕Q)⊕R=P⊕(Q⊕R)(\mathrm{P} \oplus \mathrm{Q}) \oplus \mathrm{R} = \mathrm{P} \oplus (\mathrm{Q} \oplus \mathrm{R})(P⊕Q)⊕R=P⊕(Q⊕R) となります。（証明は長いのでここでは省きます）
結合法則を踏まえると，次の命題が得られます。
命題
E~\tilde{E}E~ 上の3点 P\mathrm{P}P，Q\mathrm{Q}Q，R\mathrm{R}R が同一直線上にあるとき P⊕Q⊕R=∞\mathrm{P} \oplus \mathrm{Q} \oplus \mathrm{R} = \inftyP⊕Q⊕R=∞ である。
※ こうした楕円曲線と直線の交わりに関するトピックは，ベズーの定理を用いると，一般的なケースを含めて議論できます。興味がある方は代数曲線論の本を読んでみましょう。

楕円曲線の有理点

$y^2 = x^3 - 8$ の整数解は， $y^2 = x^3 - 8$ から定まる楕円曲線上の格子点とみなせます。以下では，楕円曲線上の格子点，つまり様々な方程式の整数解について考えます。

さらに，格子点ではなく，少々条件を緩めて有理点を考えてみます。有理点とは，各成分が有理数である点のことです。つまり，楕円曲線 $\tilde{E}$ 上の点 $\mathrm{P} (x_1 , y_1)$ について， $x_1 , y_1 \in \mathbb{Q}$ のとき， $\mathrm{P}$ を $E$ の有理点といいます。なお，無限遠点は有理点と見なします。

$E$ の有理点の集合を $E (\mathbb{Q})$ と書きます。

$E (\mathbb{Q})$ には $\tilde{E}$ の群構造がそのまま入ります。 $P,Q\in E (\mathbb{Q})$ のとき $\mathrm{P} \oplus \mathrm{Q}\in E (\mathbb{Q})$ であることを確認してみましょう。

確認

$\infty$ が登場する場合は簡単であるので， $\mathrm{P}$ ， $\mathrm{Q}$ ， $\mathrm{P} \oplus \mathrm{Q}$ が $E$ 上にあるときを考える。

$\mathrm{P} (x_1 , y_1)$ ， $\mathrm{Q} (x_2 , y_2)$ を有理点とし， $\mathrm{P} \oplus \mathrm{Q}$ を $(x_3 , y_3)$ とする。

このとき， $x_1, x_2, x_3$ は $x^3 + ax + b = (mx + n)^2$ の解であるため，解と係数の関係から $x_1 + x_2 + x_3 = m^2$ すなわち $x_3 = \left( \dfrac{x_2 - x_1}{y_2 - y_1} \right)^2 - x_1 - x_2$ である。

右辺は有理数であるため $x_3 \in \mathbb{Q}$ である。

$mx + n = \dfrac{y_2 - y_1}{x_2 - x_1} (x - x_1) + y_1$ であったことから， $y_3 = - \dfrac{y_2 - y_1}{x_2 - x_1} (x_3 - x_1) - y_1$ である。右辺は有理数であるため， $y_3 \in \mathbb{Q}$ である。

こうして $\mathrm{P} \oplus \mathrm{Q}$ は有理点である。

楕円関数の有理点については Mordell の定理という重要な定理があります。

モーデルの定理

$E(\mathbb{Q})$ は有限生成である。

すなわち， $P_1 , P_2 , \cdots , P_n \in E(\mathbb{Q})$ があって， $E(\mathbb{Z})$ の任意の点 $P$ は $P_1 , P_2 , \cdots , P_n$ の和によって表される。

例

$E : y^2 = x^3 - x + 1$ に対して $E(\mathbb{Q})$ は $(1,1)$ によって生成されます。
$E : y^2 = x^3 - 8$ に対して $E(\mathbb{Q})$ は $(2,0)$ によって生成されます。
加えて $(2,0) \oplus (2,0) = \infty$ であることから， $E(\mathbb{Q}) = \{ (2,0) , \infty \}$ となります。 $(2,0)$ のように，有限回足したら $\infty$ になる点を有限位数の点，そうでないものを無限位数の点といいます。

楕円曲線にまつわる発展的なトピック

フェルマーの最終定理

フェルマーの最終定理の証明には楕円曲線の理論が深くかかわっています。

モジュラー曲線と谷山志村予想

楕円曲線の一種の一般化にモジュラー曲線というものがあります。

モジュラー曲線とは， $\mathbb{H} = \{ z \mid z \in \mathbb{C} , \mathrm{Im} (z) > 0 \}$ を「 $\mathrm{SL}_2 (\mathbb{Z})$ の合同部分群」というもので剰余したものに，有限個の点を追加した集合です。

剰余したもの → $E$ ，有限個の点 → $\infty$ と考えると，たしかに一般化っぽいです。

特に，次の谷山志村予想が存在します。

谷山志村予想

楕円曲線はモジュラー曲線である。

※ より正確には「任意の楕円曲線に対して，あるモジュラー曲線から幾何的な構造を保つ全射が存在する」という主張です。

この予想はワイルズによって部分的に解決され，その後，ワイルズの弟子テイラーたちによって完全に解決されました。

フライ曲線

フライ曲線とは，フライによって提唱されたフェルマーの最終定理を元にする曲線です。

フライ曲線

整数 $a,b,c$ は $3$ 以上の整数 $n$ があって $a^n + b^n = c^n$ を満たすものとする。

このとき フライ曲線 とは $y^2 = x (x - a^n)(x + b^n)$ によって定義される楕円曲線である。

フライによって，フライ曲線はモジュラー曲線ではないことが予想され，実際にケン・リベットにより証明されました。

フェルマーの最終定理の証明へ

上記2つを合わせると次のような方法でフェルマーの最終定理が証明されます。

フェルマーの最終定理は不成立だと仮定する。→すなわち $a^n + b^n = c^n$ を満たす $a,b,c \in \mathbb{Z}$ が存在する。
このときモジュラーではない楕円曲線 $y^2 = x (x - a^n)(x + b^n)$ が得られる。
谷山志村予想よりすべての楕円曲線がモジュラーであることに反する。
よって最初の仮定は棄却され，フェルマーの最終定理が従う。

合同数

合同数とは，各辺の長さが有理数である直角三角形の面積になる整数のことです。

例

$3,4,5$ を3辺とする直角三角形があるため， $6$ は合同数です。
$\dfrac{3}{2} , \dfrac{20}{3} , \dfrac{41}{6}$ を3辺とする直角三角形があるため， $5$ は合同数です。

合同数については次のような強力な定理があります。

定理

$n$ が合同数であることと， $E : y^2 = x^3 - n^2 x$ に対して $E(\mathbb{Q})$ が無限位数の点を持つことは同値である。

$n$ が平方数 $N^2$ で割り切れるとき，相似な三角形を考えることで $\dfrac{n}{N^2}$ も合同数になることがわかります。

よって，以下では $n$ が平方数で割り切れないものとします。

Nagell-Lutz の定理

有限位数の点については次の強力な定理が存在します。

Nagell-Lutz の定理

$E : y^2 = x^3 + ax + b$ について $E(\mathbb{Q})$ の有限位数の点 $(x,y)$ は次を満たす。

$x , y \in \mathbb{Z}$
$y = 0$ もしくは $y^2$ は $4a^2 + 27 b^2$ を割る。

この定理より次の事実が証明できます。

事実

$E : y^2 = x^3 - n^2 x$ に対して， $E(\mathbb{Q})$ の有限位数の点は， $y = 0$ を満たす。

これらを踏まえて定理を証明します。

定理の証明

証明の概略

$n$ が合同数であることと， $a,b,c \in \mathbb{Z}$ が存在して，次の方程式を満たすことが同値である。

$\begin{cases} a^2 + b^2 = c^2\\ n = \dfrac{1}{2} ab \end{cases} \quad \cdots\cdots (\ast)$

$n$ が合同数であるとする。 $x = \dfrac{n(a+c)}{b}$ ， $y = \dfrac{2n^2 (a+c)}{b^2}$ とおくと， $y^2 = x^3 - n^2 x$ の解となる。
逆に， $E(\mathbb{Q})$ が無限位数の点を持つとする。
このとき， $y \neq 0$ としてよい。
ここで $a = \dfrac{x^2 - n^2}{y}$ ， $b = \dfrac{2nx}{y}$ ， $c = \dfrac{x^2 + n^2}{y}$ とおくと，これは $(\ast)$ を満たす。よって $n$ は合同数である。

この定理は強力ですが，楕円曲線に無限位数の点があるかどうかはどのように調べると良いのでしょうか。

実は，次のトピックである BSD 予想が深く関係しています。

BSD 予想

BSD 予想（バーチ・スウィンナートン＝ダイアー予想）はクレイ数学研究所のミレニアム懸賞問題の1つです。楕円曲線の有理点の構造と，特殊な関数の零点の様子が関係していることを主張します。

BSD予想の主張の解説も参照してください。

Mordell の定理

Mordell の定理は次のように表すこともできます。

Mordell の定理

$E(\mathbb{Q})$ は次の群のいずれかと同型である。

$\mathbb{Z}^r \oplus \mathbb{Z} / n \mathbb{Z} \quad (n = 1,2, \cdots , 10 , 12)$
$\mathbb{Z}^r \oplus \mathbb{Z} / n \mathbb{Z} \oplus \mathbb{Z} / 2\mathbb{Z} \quad (n = 2,4,6,8)$

$r$ は非負整数であり，これを $E$ のランクという。

$\mathbb{Z}^r$ ではない部分の有限群をねじれ群という。

例

$E : y^2 = x^3 - x - 1$ のとき $E(\mathbb{Q}) \simeq \mathbb{Z}$ になる。よって $E$ のランクは $1$ である。
$E : y^2 = x^3 - 8$ のとき $E(\mathbb{Q}) = \mathbb{Z} / 2\mathbb{Z}$ になる。よって $E$ のランクは $0$ である。なお， $(2,0)$ で生成される。
$E : y^2 = x^3 - 1156 x$ とする。
このとき $E(\mathbb{Q})$ は $(-2,48),(-16,120),(0,0),(34,0)$ によって生成され，特に $(0,0) \oplus (0,0)$ と $(34,0) \oplus (34,0)$ は $\infty$ になる。
これより $E(\mathbb{Q})$ は $\mathbb{Z}^2 \oplus (\mathbb{Z} / 2 \mathbb{Z})^2$ と同型である。

L関数

楕円曲線 $E: y^2 = x^3 + ax + b$ に対して $L$ 関数 $L(E,s)$ （ $E$ は楕円曲線に対応， $s$ は変数）という関数が定義されます。

定義は少々長いため，詳しくは BSD予想の主張の解説を見てください。

ここではいくつか例を紹介します。

例1

$E : y^2 = x^3 - x - 1$ のとき， $L(E,s) = 1 + 3 \cdot 3^{-s} - 2 \cdot 5^{-s} + 4 \cdot 7^{-s} + 6 \cdot 9^{-s}+ \cdots$ と続きます。

$s = 1$ のときの値を計算すると $L(E,1) = 0$ となります。

例2

$E : y^2 = x^3 - 8$ のとき， $L(E,s) = 1 + 4 \cdot 7^{-s} - 2 \cdot 13^{-s} + 8 \cdot 19^{-s} - 5 \cdot 25^{-s} \cdots$ と続きます。

$s = 1$ のときの値を計算すると $L(E,1) = 1.717315342 \dots$ となります。

例3

$E : y^2 = x^3 - 1156 x$ のとき， $L(E,s) = 1 - 2 \cdot 5^{-s} - 3 \cdot 9^{-s} - 6 \cdot 13^{-s} - 25^{-s} \cdots$ と続きます。

$s = 1$ のときの値を計算すると $L(E,1) = 0$ となります。

BSD 予想

さて，それぞれの例で $L(E,1)$ を計算しましたが，これらに法則性が見えてきますね。

$E$ のランクが $0$ であるときは $L(E,1) \neq 0$ ， $E$ のランクが $0$ ではないときは $L(E,1) = 0$ となっています。

これは一般に言えるのでしょうか。それを定式化した予想が BSD 予想となります。

BSD 予想

楕円曲線 $E$ について， $L$ 関数 $L(E,s)$ を考える。

$L(E,s)$ の $s = 1$ における零点の位数と， $E$ のランクは一致する。

零点の位数

$f(z)$ の $z = a$ における位数 $n_0$ は次のように定義される。

$f(z)$ の $z = 1$ 近傍のテイラー展開を $f(z) = \sum_{n = 0}^{\infty} a_n z^n$ とおく。 $a_n \neq 0$ となる最小の $n$ を $n_0$ とおく。

ここから1つの系が得られます。

定理

$L(E,1) \neq 0$ であれば， $E$ の有理点は有限個になる。

BSD 予想は，楕円曲線と方程式という「図形と方程式」の世界と， $L$ 関数の位数という「微積分」の世界を強く結びつける予想です。

非常に興味深い予想ですが，上述のようにかなり異なる世界の2概念を結びつけようとする問題であるため，極めて難しく現在進行形で研究されている予想です。

BSD 予想からわかること

BSD 予想を仮定すると様々なことがわかります。

例えば，先ほど紹介した合同数を完全に調べつくすことができます。

Tunnell の定理

自然数 $n$ に対して， $A_n , B_n , C_n , D_n$ を次のように定義する。

$\begin{aligned} A_n &= ( n = 2x^2 + y^2 + 32 z^2 \; \text{の整数解の個数})\\ B_n &= ( n = 2x^2 + y^2 + 8 z^2 \; \text{の整数解の個数})\\ C_n &= ( n = 8x^2 + 2y^2 + 64 z^2 \; \text{の整数解の個数})\\ D_n &= ( n = 8x^2 + 2y^2 + 16 z^2 \; \text{の整数解の個数}) \end{aligned}$

$n$ が奇数の合同数であれば $2A_n = B_n$ ，偶数の合同数であれば $2C_n = D_n$ を満たす。

BSD 予想を仮定すると逆も成立する。

Tunnell の定理に登場する方程式を $\mathrm{mod} \; 8$ で考えると， $n \equiv 5,7 \; (\mathrm{mod} \; 8)$ のとき $A_n = B_n = 0$ ， $n \equiv 6 \; (\mathrm{mod} \; 8)$ のとき $C_n = D_n = 0$ であるため $n \equiv 5,6,7 \; (\mathrm{mod} \; 8)$ のとき， $n$ は合同数ではないか？と予想されています。

より詳しく勉強したい人向けのガイド

楕円曲線について書かれた名著として，J.H.シルヴァーマン・J.テイト の『楕円曲線論入門』があります。シルヴァーマンはこの他にも数多くの楕円曲線に関する本を書いています。

N.コブリッツ の『楕円曲線と保型形式』も有名です。

LMFDB - The L-functions and modular forms database を用いることで様々な楕円曲線のランクやL関数などを調べることができます。

$157 = 8 \times 19 + 5$ であるため，合同数であることが予想されますし，実際に合同数です。それではどのような直角三角形の面積となるのでしょうか？是非検索してみてください。

楕円曲線～フェルマーの最終定理・BSD予想・合同数問題と合わせて

楕円曲線と概形

ワイエルシュトラスの標準形

楕円曲線と群構造

無限遠点

加法の定義

P，Q が $E$ 上にあるとき

$x_1 \neq x_2$ のとき

$x_1 = x_2$ ， $y_1 \neq y_2$ のとき

$x_1 = x_2$ ， $y_1 = y_2$ のとき

Q が無限遠点であるとき

P が $E$ 上にあるとき

P も無限遠点であるとき

結合法則について

楕円曲線の有理点

楕円曲線にまつわる発展的なトピック

フェルマーの最終定理

モジュラー曲線と谷山志村予想

フライ曲線

フェルマーの最終定理の証明へ

合同数

Nagell-Lutz の定理

定理の証明

BSD 予想

Mordell の定理

L関数

BSD 予想

BSD 予想からわかること

より詳しく勉強したい人向けのガイド

楕円曲線～フェルマーの最終定理・BSD予想・合同数問題と合わせて

楕円曲線と概形

ワイエルシュトラスの標準形

楕円曲線と群構造

無限遠点

加法の定義

P，Q が EEE 上にあるとき

x1≠x2x_1 \neq x_2x1​=x2​ のとき

x1=x2x_1 = x_2x1​=x2​，y1≠y2y_1 \neq y_2y1​=y2​ のとき

x1=x2x_1 = x_2x1​=x2​，y1=y2y_1 = y_2y1​=y2​ のとき

Q が無限遠点であるとき

P が EEE 上にあるとき

P も無限遠点であるとき

結合法則について

楕円曲線の有理点

楕円曲線にまつわる発展的なトピック

フェルマーの最終定理

モジュラー曲線と谷山志村予想

フライ曲線

フェルマーの最終定理の証明へ

合同数

Nagell-Lutz の定理

定理の証明

BSD 予想

Mordell の定理

L関数

BSD 予想

BSD 予想からわかること

より詳しく勉強したい人向けのガイド

P，Q が $E$ 上にあるとき

$x_1 \neq x_2$ のとき

$x_1 = x_2$ ， $y_1 \neq y_2$ のとき

$x_1 = x_2$ ， $y_1 = y_2$ のとき

P が $E$ 上にあるとき