気体分子運動論

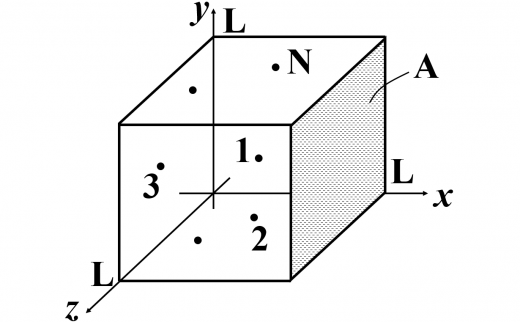
一辺の長さが $L$ の立方体の中に $N$ 個の単原子分子理想気体を入れます。また，各分子の質量を $m$ とします。

以下の条件のもとで議論を進めます。

• 分子と壁との衝突は弾性衝突とする
• 分子と壁との間に摩擦はないとする
• 分子同士の衝突は無視する

図のように $xyz$ 空間に置かれた立方体中を自由に飛び回る各分子の，壁との衝突を考えます。また，図のように立方体の $yz$ 平面に平行な面のうちの片方をA面とします。

ある1分子が1回の衝突で立方体のA面に与える力積 $I$ を求めます。分子の速度を $v$，$x$ 軸方向の速度成分を $v_{x}$ とすると，運動量変化と力積の関係より，$$m(-v_{x})-mv_{x}=-I$$

$$\therefore I=2mv_{x}$$

これを $N$ 分子に拡張して，圧力 $P$ を導きます。

1分子は，A面に衝突してから，再びA面と衝突するまでに，$\dfrac{2L}{v_{x}}$ の時間を要します。したがって，単位時間あたりにA面に与える力積は，$$2mv_{x}\cdot \dfrac{v_{x}}{2L}=\dfrac{mv^{2}_{x}}{L}$$

$N$ 分子が面Aに与える単位時間あたりの力積は，箱の中の全ての分子の $v_{x}$ 平均を $\bar v_{x}$ として，$$N\times \dfrac{m \bar v^{2}_{x}}{L}$$

力積の定義から，単位時間あたりに壁が分子から受ける力積は，壁が分子から受ける力 $F$ に他ならないので，$$F=N\dfrac{m \bar v^{2}_{x}}{L}$$

ここで，全分子の速度平均を $\bar v$ とすると，$$\bar v^{2}=\bar v^{2}_{x}+\bar v^{2}_{y}+\bar v^{2}_{z}=3 \bar v^{2}_{x}$$

$$\therefore \bar v^{2}_{x}=\dfrac{\bar v^{2}}{3}$$

すなわち，$$F=N\dfrac{m \bar v^{2}}{3L}$$

A面の面積は $L^{2}$ なので，圧力を $P$ とすると，$$P=\dfrac{F}{L^{2}}=\dfrac{Nm \bar v^{2}}{3L^{3}}$$

ここで $L^{3}=V （体積）$ と置き換えれば，$$PV=\dfrac{1}{3}Nm\bar v^{2}$$

気体分子運動論は上記のように立方体の中の気体を考えることが多いですが，球の中の気体でも同様に議論を進めることが可能です。以下に簡単に球の場合の議論を示します。

半径 $r$ の球の中に，単原子分子理想気体を入れます。

1分子が1回の衝突である面に与える力積は，$$m(-v \cos\theta)-mv \cos\theta=-I$$

$$\therefore I=2mv\cos\theta$$

1分子は球と衝突してから，再び球と衝突するまでに，$\dfrac{2r\cos\theta}{v}$ の時間を要します。したがって，単位時間あたりに面に与える力積は，全 $N$ 分子で考えると，$$2m\bar v\cos\theta\cdot\dfrac{N\bar v}{2r\cos\theta}=\dfrac{Nm\bar v^{2}}{r}$$

この右辺を $F$ とします。球の表面積は $4\pi r^{2}$ なので，圧力を $P$ とすると，$$P=\dfrac{F}{4\pi r^{2}}=\dfrac{Nm\bar v^{2}}{4\pi r^{3}}$$

ここで $\dfrac{4}{3}\pi r^{3}=V（体積）$ とすると，$$PV=\dfrac{1}{3}Nm\bar v^{2}$$

ここまでの議論で，$PV=\dfrac{1}{3}Nm\bar v^{2}$ が得られました。さて，この式を少し変更して，気体の内部エネルギーを簡単に導出してみましょう。

理想気体の状態方程式より，$PV=nRT$ なので，$$\dfrac{1}{3}Nm\bar v^{2}=nRT$$

アボガドロ定数 $N_{A}$ を用いると，$nN_{A}=N$，すなわち，$$\dfrac{1}{3}nN_{A}m\bar v^{2}=nRT$$

$$\therefore \dfrac {1}{2}m \bar v^{2}=\dfrac {3}{2}\dfrac {R}{N_{A}}T$$

ここで，ボルツマン定数を $k_{B}$　を，$k_{B}=\dfrac {R}{N_{A}}$ と定義して，$$\dfrac {1}{2}m \bar v^{2}=\dfrac {3}{2}k_{B}T$$

ゆえに，$N$ 個の単原子分子からなる気体のエネルギー $U$ は，$$U=\dfrac {3}{2}Nk_{B}T$$

また，$nN_{A}=N$ から$$U=\dfrac {3}{2}nRT$$