正弦波の意味,特徴と基本公式
正弦波の基本的な意味とそれぞれの物理量の関係性について説明します。
正弦波とは
正弦波とは
正弦波とは波動の一種です。波動とは, 振動が有限速度で空間を伝わる現象のことです。正弦波は媒質の振動が応力(外部からの力に抵抗する力)によって伝わる力学的な現象の一つです。
時刻 , 位置 における正弦波の式は
( : 角振動数, : 伝播速度)
正弦波の公式は を用いて表すことが多いので, 正弦波を「 波」「正弦曲線」「サインカーブ」ということもあります。

この記事では
- 上記の公式がどうしたら得られるのか
- 違う表式はないのか
ということを含め, 波動分野の正弦波に関して詳しく説明します。
この記事に関連するQ&A
正弦波の表し方
正弦波の表し方
まず正弦波の基本的な特徴について理解しましょう。
ここを理解すると, 自分で正弦波の表式を作ったり自分が欲しい形に変形したりすることができるようになります。
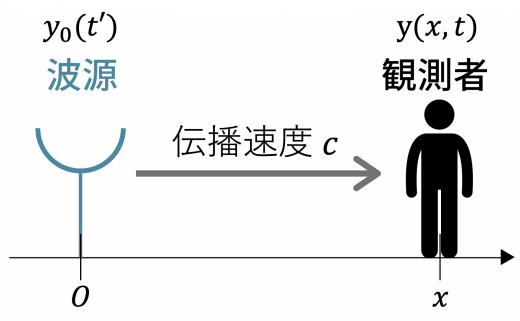
ある時刻 に位置 の「波源」から波
が出たという状況を考えましょう。
この時刻 に波源を出た波が, 時刻 に位置 にいる「観測者」に届くとします。
観測者が観測する波の式は以下のようになります。
変形の途中で と置きました。 の意味については後述します。
また時刻 と の間には以下の関係式が成り立ちます。
以上の2つの式から を消去すると, 次の式が与えられます。
これが正弦波の一般的な表式です。
式の中に含まれる物理量をまとめます。
| 物理量 | 意味 |
|---|---|
| 位置 | |
| 時刻 | |
| の絶対値は振幅を表す | |
| 角振動数 | |
| 伝播速度 | |
| 初期位相 |
※式の途中に現れた は振幅の減衰率を表します。 は を満たす値で, 波が伝わる過程でどれくらい振幅がすり減るかを表す値です。特に断りがない場合には であると考えます。
式に登場する物理量が多いので覚えて理解するのに時間がかかるかもしれません。
「自分の知っている正弦波の式ではない」と驚かないでください。正弦波の式には様々は表し方があるのです。この記事を読み終わるころには正弦波の様々な表現方法について理解できるようになっていますよ。
位相
正弦波の表式をもう一度みてみましょう。
この表式で の中の部分を 波の位相と呼びます。
特に , での波の位相を初期位相と呼びます。
位相 を用いると, 波の式は以下のように与えられます。
位相 は 時刻 , 位置 での波の波形(山や谷)を表す非常に重要な物理量です。
位相(右辺)を理解することで正弦波(左辺)を理解することができるのです。
正弦波の基本的な特徴
正弦波の基本的な特徴
この節では,正弦波の基本的な特徴を説明します。
正弦波の式は
で与えられます。
まずは「振幅」と「位相速度」を理解しましょう。
- 振幅:
- 位相速度: を満たす,位置 の移動速度のこと
振幅とは波の振れ幅の最大値を表す値で, 正の値をとるように定義します。
位相速度は正弦波が進む速度のことだと理解すれば良いでしょう。
位相速度とは, その定義に戻ると
を満たす位置 の移動速度のことです。
さて, 上式の両辺を で微分した方程式を解くと正弦波の位相速度が求められます。
この場合, 位相速度 は伝播速度 と一致していることがわかります。
以下ではさらに波の位相の特徴をみていきます。
位相(位置を固定した時)の特徴
位置 をある位置 に固定して, その位相 を観察しましょう。

と表すことができます。 は に依らない定数です。
この位相の表式を見ると, 次の物理量の特徴がとても明瞭になります。
| 物理量 | 意味と考え方 |
|---|---|
| 角振動数 | 単位時間あたりの位相変化 が になった時に 位相は だけ増える。 |
| 振動数 | : 単位時間あたりの振動回数。 単位時間あたり だけ 位相が増えるので, これを で割れば 単位時間あたりの振動回数になる。 |
| 周期 | : 1回振動するのに要する時間。 位相が 増えるのは が になったとき。 |
※「1回振動する」とは「波の位相が 増える」ことだと考えましょう。
位相(時刻を固定した時)の特徴
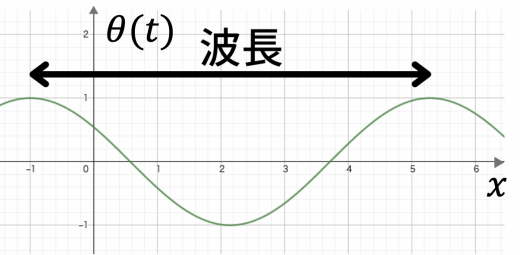
今度は逆に, 時刻 をある時刻 に固定して, その位相 を観察しましょう。
と表すことができます。 は に依らない定数です。
が固定された位相の表式からは, 次の物理量の特徴を掴むことができます。
| 物理量 | 意味と考え方 |
|---|---|
| 波長 | 山と山(谷と谷)の間隔。 定義より, の関係性がわかる。 |
| 波数 | 単位長さあたりの位相変化。 が になった時に 位相は だけ変化する。 |
正弦波の様々な表し方
正弦波の様々な表し方
前節で位相の特徴とそこからわかる物理量の意味・物理量同士の関係性がわかりました。
ここで改めて全てまとめます。
| 物理量 | 意味と考え方 |
|---|---|
| 角振動数 | 単位時間あたりの位相変化 が になった時に 位相は だけ増える。 |
| 振動数 | : 単位時間あたりの振動回数。 単位時間あたり だけ 位相が増えるので, これを で割れば 単位時間あたりの振動回数になる。 |
| 周期 | : 1回振動するのに要する時間。 位相が 増えるのは が になったとき。 |
| 波長 | 山と山(谷と谷)の間隔。 定義より, の関係性がわかる。 |
| 波数 | 単位長さあたりの位相変化。 が になった時に 位相は だけ変化する。 |
これらの物理量を用いると, 波の位相 は様々な表現方法で表すことができます。
個人的にはこれらの表現方法を「全て暗記する」というのはあまりおすすめできません。それよりも「それぞれの物理量の意味と関係性を理解して, 自分が使いたい形に変形する」ことが重要です。
正弦波は 波と呼ばれるように、グラフがサインの曲線の形になっていることが最大の特徴です。上で紹介した正弦波の公式をただ丸暗記して使うのではなく, グラフを手で描くことがとても大切です。
「波動」の分野を攻略するためには, 正弦波の式をみた瞬間に
- 振幅
- 位相速度
- 周期
- 波長
などの物理量の値をすぐに算出し, 頭の中に正弦波の波形のグラフを描けるようになりましょう。
今は難しいかもしれませんが、以下の例題をこなせばすぐに身に付けることができます。
正弦波
の振幅, 位相速度, 周期, 波長を求めよ。
- 振幅: 10(※絶対値をとることを忘れずに)
正弦波の位相部分は
である。位相速度の定義にしたがって
の方程式を考えると,
- 位相速度:
を固定した時に,位相が 増えるのに要する時間を考えれば,
- 周期:
を固定した時に,原点 から位相が 増える次の座標を考えれば,
- 波長:
正弦波を で表すこともあります。この場合、 波とも呼びます。正弦波だからと言って必ず とは限らないことに注意が必要です。時と場合に応じて扱いやすい表式で表すのがセオリーです。










