入射波と反射波（固定端反射・自由端反射）

波の基本性質の一つに反射が挙げられます。反射とは波がある境界面で跳ね返る現象のことです。

跳ね返る前の波を入射波（Incident wave）, 跳ね返った後の波を反射波（Reflected wave）といいます。

以下のような入射波 $y_i(x,t)$ と反射波 $y_r(x,t)$ を考えてみましょう。

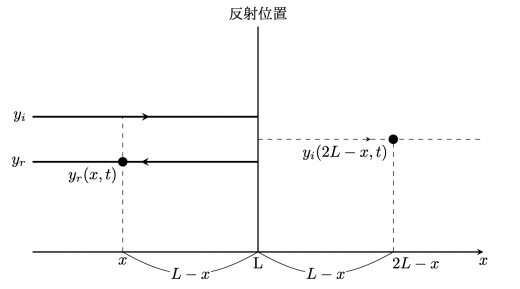
反射波 $y_r(x,t)$ は反射が起こったことで $y_i(2L-x,t)$ が届いたものだとみなします。

突然 $2L-x$ という値が出てきた混乱した方もいるかもしれません。位置 $x = L$ で跳ね返って位置 $x$ まで届くとき, その長さは $L-x$ なので, 壁がなく波が直進した場合に波が到達しているであろう位置は $L + (L - x) = 2L-x$ です。

本当は（壁がなければ）反射位置よりも奥側にあった波が反射によって手前に届いているだけとみなすのです。

自由端反射と固定端反射

反射には大きく分けて

1. 自由端反射
2. 固定端反射

の二種類があります。

この二種類で異なる点は「反射位置で波の位相が変わるか」という点です。

反射位置で波の位相がずれない場合を自由端反射, 波の位相が $\pi$ だけずれる（位相が反転する）場合を固定端反射といいます。

以下でそれぞれ詳しくみていきましょう。

入射波 $y_i(x,t)$ を

$$y_i(x,t) = A \sin \left\{ 2 \pi \left( \dfrac{t}{T} - \dfrac{x}{\lambda} \right) + \alpha \right\}$$

と表します。

※正弦波（進行波）の表現方法についての詳細はこちら→正弦波の意味，特徴と基本公式

先ほど述べたように、反射波は反射位置 $x=L$ での折り返しによって $y_i(2L-x,t)$ が届いたものだと考えましょう。

上の関係式から、反射波は

$$\begin{aligned} y_r(x,t) &= y_i(2L-x,t) \\ &= A \sin \left\{ 2 \pi \left( \dfrac{t}{T} - \dfrac{2L-x}{\lambda} \right) + \alpha \right\} \end{aligned}$$

と表すことができます。

自由端反射の場合, 反射波のグラフは反射位置 $x = L$ で入射波のグラフを折り返したものになります。

特に, 反射位置 $x = L$ においては

$$y_r(L,t) = y_i(L,t)$$

が成り立ちます。すなわち, 入射波と反射波の変位が同じということです。

そのため自由端反射の境界では入射波と反射波の合成波は強め合っていると言えます。

自由端反射の場合と同様に, 入射波 $y_i(x,t)$ を

$$y_i(x,t) = A \sin \left\{ 2 \pi \left( \dfrac{t}{T} - \dfrac{x}{\lambda} \right) + \alpha \right\}$$

と表します。

固定端反射の場合, 位相が $\pi$ だけずれることがポイントです。

位相が $\pi$ だけずれるとは, 入射波の位相

$$\theta_i = 2 \pi \left( \dfrac{t}{T} - \dfrac{x}{\lambda} \right) + \alpha$$

に対して, 反射波の位相は

$$\begin{aligned} \theta_r &= \theta_i + \pi \\ &= 2 \pi \left( \dfrac{t}{T} - \dfrac{x}{\lambda} \right) + \alpha + \pi \end{aligned}$$

と書き表せるということです。

これらの関係式から

$$\begin{aligned} y_r(x,t) &= y_i(2L-x,t) \ \text{の位相が反転したもの} \\ &= A \sin \left\{ 2 \pi \left( \dfrac{t}{T} - \dfrac{2L-x}{\lambda} \right) + \alpha + \pi \right\} \\ &= - A \sin \left\{ 2 \pi \left( \dfrac{t}{T} - \dfrac{2L-x}{\lambda} \right) + \alpha \right\} \\ &= -y_i(2L-x,t) \end{aligned}$$

となり, 先ほど紹介した関係が成り立つことが示せました。

自由端反射の場合, 反射波のグラフは反射位置 $x = L$ で入射波のグラフを折り返したものになります。

特に, 反射位置 $x = L$ においては

$$y_r(L,t) = - y_i(L,t)$$

が成り立ちます。すなわち, 入射波と反射波の変位は反転しています。

そのため固定端反射の境界では入射波と反射波の合成波は弱めあっており, その変位は $0$ であるという特徴があります。

入射波が正弦波で書き表せる時, 入射波と反射波の合成波が定常波になる場合があります。

定常波とは時刻によらずにその場にとどまっているように見える波のことです。まだ定常波のことを知らない方は先にこちらの記事を読まれると良いです→定常波・合成波・重ね合わせの原理

さて, 以下では入射波と反射波の合成波が定常波になる場合の式を追っていきましょう。

入射波（定常波）:

$$y_i(x,t) = A \sin \left\{ 2 \pi \left( \dfrac{t}{T} - \dfrac{x}{\lambda} \right) + \alpha \right\}$$

自由端反射による反射波:

$$y_r(x,t) = A \sin \left\{ 2 \pi \left( \dfrac{t}{T} - \dfrac{2L-x}{\lambda} \right) + \alpha \right\}$$

と書き表すことができます。

合成波 $y(x,t)$ は重ね合わせの原理から,

$$y(x,t) = y_i(x,t) + y_r(x,t)$$

で表せます。実際に計算してみると,

$$\begin{aligned} y(x,t) &= y_i(x,t) + y_r(x,t) \\ &= A \sin \left\{ 2 \pi \left( \dfrac{t}{T} - \dfrac{x}{\lambda} \right) + \alpha \right\} + A \sin \left\{ 2 \pi \left( \dfrac{t}{T} - \dfrac{2L-x}{\lambda} \right) + \alpha \right\} \\ &= 2A \cos \left( 2 \pi \dfrac{L-x}{\lambda} \right) \sin \left\{ 2 \pi \left( \dfrac{t}{T} - \dfrac{L}{\lambda} \right) + \alpha \right\} \end{aligned}$$

これは紛れもなく定常波の式です。

反射が固定端反射の場合も同様の計算によって正弦波ができることを示せます。

固定端反射による反射波:

$$y_r(x,t) = - A \sin \left\{ 2 \pi \left( \dfrac{t}{T} - \dfrac{2L-x}{\lambda} \right) + \alpha \right\}$$

の式を用いて計算してみると,

$$\begin{aligned} y(x,t) &= y_i(x,t) + y_r(x,t) \\ &= A \sin \left\{ 2 \pi \left( \dfrac{t}{T} - \dfrac{x}{\lambda} \right) + \alpha \right\} - A \sin \left\{ 2 \pi \left( \dfrac{t}{T} - \dfrac{2L-x}{\lambda} \right) + \alpha \right\} \\ &= 2A \sin \left( 2 \pi \dfrac{L-x}{\lambda} \right) \cos \left\{ 2 \pi \left( \dfrac{t}{T} - \dfrac{L}{\lambda} \right) + \alpha \right\} \end{aligned}$$

となるので, やはり正弦波となっています。

特に, 初期位相 $\alpha = 0$ の場合には, 正弦波の入射波とその反射波によってできる定常波の式は以下のように表せます。

自由端反射の場合と固定端反射の場合では, $\sin$ と $\cos$ が入れ替わっているだけということに気が付きましょう。この関係は固定端反射で位相が反転していることに由来します。