横波 縦波
意外と違いを区別できていない人が多い「横波」と「縦波」について解説します。
それぞれの違いや特徴を全てわかりやすく説明します。
この記事に関連するQ&A
縦波と横波の違い
縦波と横波の違い
縦波と横波を区別することはとても簡単です。縦波と横波の違いは,
- 振動方向(変位)に対して波がどの向きに進むか?
ということだけです。
波の振動方向(変位)が波の伝播方向(進む向き)に
- 垂直な場合を横波
- 平行な場合を縦波
という。

波の振動方向と進む向きの関係については, 動画で見るとより理解しやすいです。以下の動画はレインボースプリングを使って横波と縦波を模式的に表現しています。
縦波の場合, 波は画面の左から右に進みながら, その振動方向も画面の左右方向です。一方で横波の場合, 波は画面の左から右へ進む一方で, 振動方向は画面の上下方向です。
この動画での縦波と横波の表現はあくまで模式的なものなので, 厳密に正確であるとは言えませんが
- 横波は振動方向に垂直な向きに波が伝わる
- 縦波は振動方向と平行に波が伝わる
ということが理解できれば大丈夫です。
横波と縦波の具体例
横波と縦波の具体例
これまで「波」と聞いた時に頭の中に「横波」の絵を思い浮かべた方がほとんどではないでしょうか?
前節で「横波」「縦波」と聞いてまだあまりピンと来ていないかもしれません。この節では横波と縦波の具体例を挙げます。
案外、日常生活には縦波も横波も馴染みがあることがわかります。
横波の例
横波は波の振動方向に対して垂直に伝わる波です。
例で言うと, 二人でロープの両端を持って一直線に並び、水平方向に腕をふった時にできる波が横波です。
横波の例には次のようなものが挙げられます。
- ロープを伝わる波
- 弦(バイオリンの弦の振動)
- 光
- 電磁波(光を含む)
- 水面の波
- 地震(S波)
光は電磁波の一種で, 例えは太陽光なども含みます。また、紫外線や赤外線・X線なども電磁波の一種ですから横波です。
光が横波であることは「偏光」という現象を学習すると非常に納得がいくようになります。波が偏光を示すのはその進行方向と垂直な方向に振動方向・振動面があるからです。偏光は横波にしか見られない波動現象であることがわかります。
縦波の例
縦波は波の振動方向に対して平行に伝わる波です。
縦波は横波と比べると少しイメージしづらいですが, 次のような例が挙げられます。
- 音波(空中)
- 音波(水中)
- 地震(P波)
これら縦波に共通する点は「疎密を作る」という点で、横波には見られない特徴です。
縦波の疎密についてはこの後詳しく説明します。
地震は横波と縦波の両方
上でも例として挙げていますが, 地震は横波と縦波の両方が混ざった現象です。
地震の揺れは、
- 最初に縦波のP波(Primary Wave)が到達し(初期微動)、
- 次に横波のS波(Secondary Wave)が到達します(主要動)。
この地震の例でもわかるように、縦波の速度は横波の速度よりも速いことが多いです。(※必ずそうであるとは限りません。)
地震の縦波・横波については以下の「よくある誤解」に十分注意するようにしてください。
最初に縦波のP波が届くから地震は「縦揺れ」、その後に横波のS波が届くから地震は「横揺れ」 する。
「縦」「横」の単語が共通していることが原因だと思いますが, 誤解です。
「縦揺れ」「横揺れ」といった現象は「震源地・震央」と「観測者」の位置関係などに依存するもので, 縦波・横波とは一切関係がありません。
あくまで縦波は「波がその振動方向に対して平行に伝わる波」というだけで、地上にいる人間を縦に揺らすのか(あるいは横に揺らすのか)ということとは全く関係がないのです。
縦波(疎密波)の密度変化
縦波(疎密波)の密度変化
縦波は空気分子を振動させ, 空気中の分子の分布に「疎」と「密」を作り, その疎密が伝播する現象です。この特徴から, 縦波のことを「疎密波」と呼ぶ場合もあります。
- 疎: 空気分子の分布がまばらになっていて, 密度が小さい点のこと
- 密: 空気分子の分布が密集していて, 密度が大きい点のこと
縦波を横波に変換した図が与えられて「最も疎なのはどこか?」という問題をよく見かけます。
その解答で
- 上向き変位を右へ
- 下向き変位を左へ
という解説がよくなされています。その意味を正しく理解せずに丸暗記してしまっていませんか?
そのようなテクニックを意味を理解せずに丸暗記してしまうと応用問題に対応できないので、本節で式を追いながらしっかり理解してしまいましょう。
疎密波の密度
下図のように空気中にとても小さい円柱の領域(面積 , 高さ )を考えて, その密度が微小変化(わずかに変化)するとしましょう。

は 時刻 の位置 における気体分子の 軸方向への変位です。
図中では, ある時刻 において気体分子が位置 から だけ, 位置 から だけ変位している様子が示されています。
振動がないときの密度を とします。
振動前後の質量保存則より
が成り立ちます。ただし とは振動後の円柱内部の平均密度を表します。
ここで微小変位 について の極限(円柱の高さを限りなく に近づける操作)を考えます。
の時,
であることから,
とすることができます。
のような表記を「偏微分」といいます。
は とほとんど同じ意味です。 時刻 を 位置 に依存しない定数だとみなして(固定して), 変位 を 位置 で微分するという意味です
実際には も の関数ですが、偏微分においては はただの定数だと思って だけを で微分するのです。
さらに詳しい偏微分の説明はこちら→偏微分の意味と計算例・応用
通常, であることが多い(つまり微小領域で密度は突然大きく変位しない)ので
以上から, 縦波(疎密波)の密度 は以下のように得られます。
縦波(疎密波)の密度 は
で与えられる。
さらに密度変化 を定義すると, 密度変化率 は
のように表されます。
密度変化率 が正であれば「密」, 負であれば「疎」ということです。
以上から, 縦波(疎密波)の「疎密」には以下の関係があるとわかります。
ただし, は縦波を横波表示した グラフにおいて, その曲線の傾きを表す。
ここまでの式の意味を理解できた人は縦波を横波に変換した図が与えられても何も怖くありません。
注目しなければいけないのは, その図中の各点で (グラフの傾き)が正なのか負なのかということだけなのです。
縦波を横波表示したグラフの各点において
- グラフの傾きが正であれば「疎」
- グラフの傾きが負であれば「密」
です。
「最も疎なのはどこか?」という問題であれば「グラフの傾きが最大になる点はどこか?」と聞かれているだけなのです。
同様に「最も密なのはどこか?」という問題であれば「グラフの傾きが最小になる点はどこか?」と聞かれているだけなのです。
もう変なテクニックに頼る必要はありません。縦波の本質を理解して以下の問題に取り組んでみてください。
縦波の疎密に関する問題(簡単)
図は媒質中をx軸の正の向きに伝わる縦波の波形である。ただし, 媒質の変位を 軸の正の向きの変位を正として表したものである。

媒質の密度が最大となっている 座標はどこか。
媒質の密度が最小となっている 座標はどこか。
グラフの傾きが最小の点を選べば良い。よって
グラフの傾きが最大の点を選べば良い。よって
縦波の疎密に関する問題(応用)
図は媒質中をx軸の正の向きに伝わる縦波の波形である。ただし, 媒質の変位をx軸の正の向きの変位を正として表したものである。
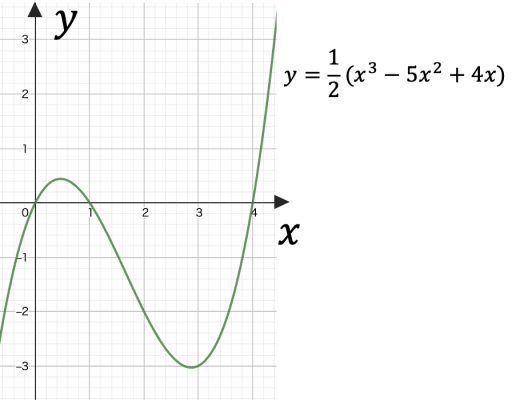
媒質の密度が最大となっている 座標はどこか。
媒質の密度が最小となっている 座標はどこか。
各点 におけるグラフの傾きは
グラフの傾きが最小の点を選べば良い。よって
グラフの傾きが最大の点を選べば良い。よって
縦波の疎密を判断するためにはとにかくグラフの傾きを見れば良いということがわかりました。
「綾波レイ」は縦波の例でもなければ、横波の例でもありません。










