波の干渉・回折

複数の波が重なり合って新しい波形を作るとき, 波は互いに強め合ったり弱め合ったりします。このような波どうしの相互作用のことを波の干渉といいます。

特に, 同じ光源から発せられた波や周波数が近い波どうしは干渉を起こしやすく, 「コヒーレントである」といいます。波の「うねり」現象はまさにコヒーレントな波どうしが起こす現象の一つです。

波が障害物の背後に回り込む現象のことを波の回折といいます。一見すると幾何学的には到達できないであろう位置にまで波が伝わる現象です。

以下では干渉と回折の代表例を紹介します。

干渉の代表例

干渉には次のような例があります。

• 薄膜による光の干渉（薄膜干渉）
• くさび形空気層における光の干渉
• ニュートンリング
• ヤングの実験(回折格子による干渉)

これらの現象はいずれも高校物理では頻出で重要です。以下でそれぞれ詳しく解説するのでよく理解しておきましょう。

※最重要な「ヤングの実験」については別記事で説明します。→ヤングの干渉実験

回折の代表例

• 単スリットでの回折
• ヤングの実験(回折格子による干渉)

日常生活でいうと, ドアの向こうの声がドアの下のわずかな隙間を通して聞こえてくる現象も波（音波）の回折と言えます。

回折は光に限らず, 音波や水の波や電磁波でも観測される現象です。

高校物理では「回折」について問われることは多くなく, 「干渉」とセットで問われる現象です。干渉と合わせて理解しておきましょう。

波の干渉をよく理解するために, 同光源の波の位相差について理解しておきましょう。

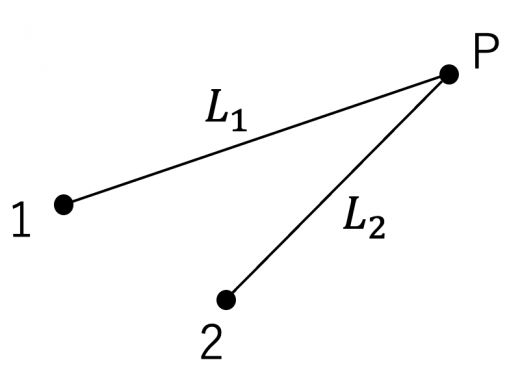
二つの波がそれぞれ経路長 $L_1, L_2$ を経て, 点 $P$ で合流するとします。

点 $P$ において

• 波1の位相: $\theta_1 = \omega (t - \dfrac{L_1}{c}) = \omega t - \dfrac{2 \pi}{\lambda} L_1$

• 波2の位相: $\theta_2 = \omega (t - \dfrac{L_2}{c}) = \omega t - \dfrac{2 \pi}{\lambda} L_2$

と表せます。

点 $P$ での位相差 $\phi$ は, 経路差 $\varDelta L$ を用いて以下のように表されます。

$$\begin{aligned} \phi &= \theta_1 - \theta_2 \\ &= -\dfrac{2 \pi}{\lambda}(L_1 - L_2) \\ &= -\dfrac{2 \pi}{\lambda} \varDelta L \end{aligned}$$

光学距離を考えるよりも, 経路差とそこから計算される位相差を考える方が全体として見通しがよく間違いにくいです。

この位相差と経路長の関係を理解した上で, 以下の干渉・回折の具体例に進みましょう。

薄膜に波が入射すると, 薄膜の表面で反射した反射光と, 薄膜の底で反射した反射光が干渉します。

以下の図をみてください。

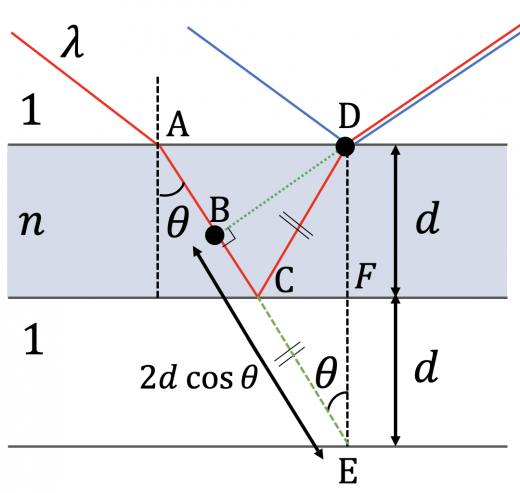
波長 $\lambda$ の光（赤色・青色）が屈折率 $n$ の薄膜に入射します。赤色の入射光は薄膜の底で反射する反射光,青色の入射光は薄膜の表面で反射する反射光です。

先ほど紹介した関係式

$$|\phi| = \dfrac{2 \pi}{\lambda} \varDelta L$$

に当てはめて考えるためには

1. 経路差 $\varDelta L$ はいくらか？
2. 波の波長はいくらか？

を把握することが必要です。

「1. 経路差 $\varDelta L$ はいくらか？」についてはどうでしょうか。

経路差は $\varDelta L = 2d \cos \theta$ です。

図形の性質を見つけましょう。赤色の反射光が薄膜の底（点 $\mathrm{C}$）で反射しますが, その反射光を延長した補助線（辺 $\mathrm{CE}$）を書いてみると二等辺三角形 $\triangle \mathrm{CED}$ ができます。

底辺 $\mathrm{DE} = 2d$ で, $\mathrm{CD} = \mathrm{CE}$ が成り立ちます。錯角の関係から, その二等辺三角形 $\triangle \mathrm{CED}$ の底角 $\angle \mathrm{E}$ は屈折角 $\theta$ と一致します。

点 $\mathrm{B}$ は, 点 $\mathrm{D}$ から辺 $\mathrm{AC}$ に下ろした垂線との交点です。ホイヘンスの原理の通り, 点 $\mathrm{B}$ と点 $\mathrm{D}$ で位相が一致しています。

そこで, 今知りたいのは経路差 $\mathrm{BC} + \mathrm{CD}$ であるとわかります。ここまで明らかにした関係式から, $\mathrm{BC} + \mathrm{CD} = \mathrm{BE}$ が成り立ちます。

したがって, 直角三角形 $\triangle \mathrm{DBE}$ に注目すると, 経路差は

$$\mathrm{BE} = 2d \cos \theta$$

とわかります。

「2. 波の波長はいくらか？」についてはどうでしょうか。

ここで安易に $\lambda$ と答えると間違えてしまいます。赤色の反射光は屈折率 $n$ の媒質中を進んでいますから, 波の波長は $\lambda / n$ です。

さて, これらを当てはめて考えてみると, 赤色の反射光と青色の入射光の位相差の大きさは

$$|\phi| = \dfrac{2 \pi}{\lambda / n} \cdot 2d \cos \theta$$

と表されます。

この先で波の干渉（強め合い・弱め合い）を考えるに当たって, もう一つだけ注意点があります。それは「青色の経路では反射の際に位相が $\pi$ だけずれる」ということです。

一般に, 反射における位相の変化については以下の事実が知られています。

空気中の屈折率が1, 薄膜の屈折率が $n \ (> 1)$ なので, 青色の経路での反射は「屈折率が小さい媒質から大きい媒質に向かう境界面での反射」に該当します。したがって, 青色の経路では反射の際に位相が $\pi$ だけずれるということになります。

したがって, 赤色の反射光と青色の反射光の位相差の大きさは

$$|\phi| = \dfrac{2 \pi}{\lambda / n} \cdot 2d \cos \theta - \pi$$

と表されます。

ここから干渉の関係は次のようにまとめられます。

薄膜による光の干渉の理解で重要なポイントは

• 経路差は $2d \cos \theta$
• 薄膜中での波の波長は $\lambda / n$
• 表面での反射では位相が $\pi$ だけずれる

です。

「薄膜干渉」と同様に

$$|\phi| = \dfrac{2 \pi}{\lambda} \varDelta L$$

に当てはめて計算しましょう。

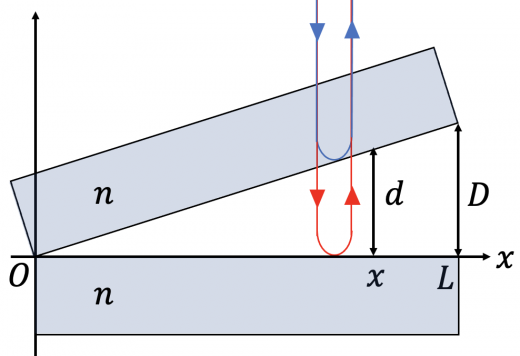
今回は赤色の経路で「屈折率が小さい媒質から大きい媒質に向かう境界面での反射」が起きているので, 位相が $\pi$ だけずれるということになります。

経路差は $2d$, 波長は空気中なので $\lambda$ です。

「薄膜干渉」と比べると「くさび形空気層における光の干渉」の例はとてもシンプルに位相を計算できます。

まとめると以下のようになります。

なお, 図中の $x, D, L$ を用いる場合は以下の関係式を使います。

$$x:d = L:D \iff d = \dfrac{D}{L}x$$

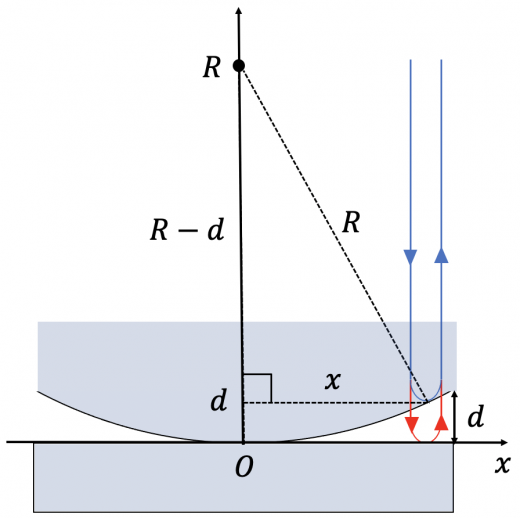
図のように, 平面ガラスの上に曲率半径が大きな凸レンズを置いた状況を考えます。

この装置に光を直上から当てると「強め合い」と「弱め合い」による干渉膜が同心円状（環状）に交互に並びます。この模様をニュートンリング(ニュートン環)といいます。

ニュートンリングが生成される原理も「波の干渉」です。これまでと同じように強め合い・弱め合いの関係を理解するとニュートンリングの原理がよくわかります。

さて, 経路差は図より $\varDelta L = 2d$ ですが, $\varDelta L$ と 曲率半径 $R$ の関係を求めましょう。

三平方の定理から

$$(R - d)^2 + x^2 = R^2 \\ \therefore -2Rd + d^2 + x^2 = 0$$

$d$ は非常に小さく, $d \ll 1$ と考えて切り捨てましょう。

$$-2Rd + d^2 + x^2 = 0 \\ -2Rd + x^2 = 0 \\ \varDelta L = 2d = \dfrac{x^2}{R}$$

波長は空気中なので $\lambda$ です。

今回は赤色の経路で「屈折率が小さい媒質から大きい媒質に向かう境界面での反射」が起きているので, 位相が $\pi$ だけずれるということになります。

以上から,　ニュートンリングにおける波の干渉の条件は以下のようにまとめられます。

明線の位置は

$$x_{\text{明}} = \sqrt{(m + \dfrac{1}{2}) \lambda R}$$

暗線の位置は

$$x_{\text{暗}} = \sqrt{m \lambda R}$$

明線と暗線の間隔は

$$x_{\text{明}} - x_{\text{暗}} = \left( \sqrt{m + \dfrac{1}{2}} - \sqrt{m} \right) \sqrt{\lambda R}$$

と表されます。

実際にニュートンリングの実験をするとよくわかりますが, ニュートンリングは曲率半径が大きいレンズを使用した方が明線と暗線の間隔が広がるため観察しやすいです。

また, リングの中央 $x = 0$ は常に暗線となります（$m = 0$）。