ヤングの干渉実験

ヤングの干渉実験とは1805年頃にイギリスの物理学者トマス・ヤングによって行われた光の干渉の性質を証明した実験です。単に「ヤングの実験」ということもあります。

光源からの光を複スリットに通すと, その先に設置してあるスクリーン上に明線と暗線が等間隔で交互に並ぶ干渉縞ができるという現象が観測されます。

ヤングの実験は光の波動性を示す重要な実験です。物理学の歴史の中でも「光の解釈」について語る上では外せない実験です。その歴史的経緯について以下で触れておきます。

歴史的経緯よりも早く実験の内容を知りたい方は次の見出しまでスキップしてください。

歴史的経緯

物理学の世界において「光の正体は何か？」という議論は長きに渡って展開されていました。「ヤングの干渉実験」はその議論の中で歴史的に重要な意味を持つ実験であるとも言えます。

18世紀頃, ホイヘンスが「ホイヘンスの原理」の中で提唱した「波動説」とニュートンが主張する「粒子説」の二つの説が対立しており, 光の正体は未知とされていました。

1805年頃, ヤングは「ヤングの干渉実験」によって「光は干渉する」ということを示したのです。干渉は波の性質なので, ヤングの干渉実験によって「光は波動である」という説が大きく強まったのです。

ヤングの干渉実験の後, フレネル, フーコー, フィゾー, ファラデー, マクスウェル, ヘルツといった著名な物理学者たちの実験によって「光の波動性」を裏付ける重要な実験結果が得られました。これらの背景から, 「光は波動である」という認識が強く広まっていたのです。

ただ光が本当に”純粋な”波動であるとすると, どうにも上手く説明できない現象も同時に観測されており, 物理学者の頭を悩ませていました。

そこに現れた稀代の天才がアインシュタインです。アインシュタインが主張した「光量子仮説」は「光の粒子説」を主張するものでした。光量子仮説によって再び光の「粒子説」の議論が再燃しました。

最終的にアインシュタインは光は粒子と波動の二重性を持つという結論を出し, これが今日に至るまで広く支持されている光の解釈です。アインシュタインは光量子仮説によって1921年のノーベル物理学賞を受賞しています。

アインシュタインによる光量子仮説は1905年に提唱されました。これはちょうどヤングの干渉実験から100年が経過した頃でした。

ヤングの実験は以下の図のような装置で行われます。

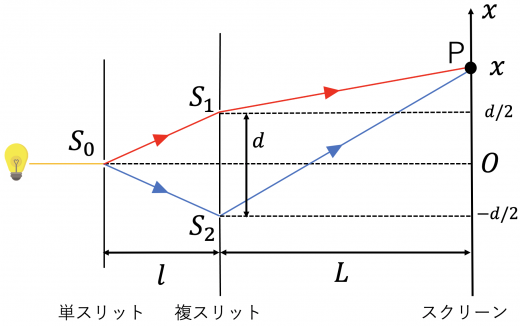
光源を出た光は単スリット $S_0$ に入射します。単スリットに入射した光は回折し, その後ろにある複スリット $S_1, S_2$ に入射します。

複スリット（二重スリット）で光は回折し, それぞれのスリットからの光に分かれます。

2つの光は複スリットで回折した後スクリーンに到達しますが, それぞれの光はスクリーン上の各位置で一定の位相差を持っているので干渉（= 強め合い・弱め合い）が起きるという原理です。

単スリット・複スリットとは

ヤングの実験装置に登場する「単スリット」と「複スリット」について理解しておきましょう。

スリットとは隙間のことです。スリットには「単スリット」と「複スリット」の二種類があります。どちらも高校物理の範囲で理解しておかなければいけない装置です。

複スリットのうち, 特にスリットの数が2つの場合に二重スリットといいます。ヤングの実験では二重スリットを用います。

ヤングの実験においては

1. 単スリットは複スリットに入る光の位相を揃える
2. 複スリットは入射光を二つの光路の光に分解する

と理解しておけば十分です。

※現実的には単スリット・複スリットの扱い・理解は非常に難しく, 厳密には上記の解釈は正しいと言えません。しかしながら, 少なくとも高校物理・大学受験の物理の範囲においては上述の解釈で十分です。

ヤングの実験は複スリットによる干渉実験ということができます。ただし, 単スリットでも光の干渉は観測されます。単スリットにおける光の干渉については別の記事で紹介します。

複スリットの役割

複スリットの役割は, 1つの光源からの光を2つの光路に分解することです。

ここで

• 「複スリットを使わずに, 光源を2つにしたら良いのではないか？」

という考えもあるでしょう。

ですが、それではヤングの干渉実験は上手くいかないのです。実は2つの点光源からの光は干渉することはありません。光源からの光には無数の発光体から発せられる様々な位相の光が混在しています。したがって別々の光源からの光を合成しても, 強め合い・弱め合いが複雑に起こるため綺麗な干渉縞が観測されません。

そのため, 単一の点光源からの光を分解する複スリットが必要となります。

ここからヤングの実験の基本原理を説明します。頻出テーマなので自分で1から導出できるようにしておきましょう。

単スリット $S_0$, 複スリット $S_1, S_2$ が距離間隔 $\ell$ で, 複スリット $S_1, S_2$とスクリーンが距離間隔 $L$ で置かれています。$S_1, S_2$ の間隔を $d$ とします。

スリット間隔 $d$ は $\ell, L$ と比べて十分に小さい値です。

スリットは $S_0S_1 = S_0S_2$ となるように配置し, スリット・複スリット・スクリーンのいずれの衝立も $y$ 方向に平行になるように設置します。この時, $S_0$, $S_1S_2$の中点, スクリーンの原点 $O$ が一直線状に並びます。

$S_0 \to S_1 \to P$ の経路を通る光と $S_0 \to S_2 \to P$ の経路を通る光の位相差がスクリーン上に干渉縞を生成します。

スクリーン上での位相差を考えるために, まず2つの経路の経路差を計算します。

経路差は

$$\begin{aligned} & S_2P - S_1P \\ &= \sqrt{L^2 + \left( x + \dfrac{d}{2} \right)^2} - \sqrt{L^2 + \left( x - \dfrac{d}{2} \right)^2} \\ &= L \left[ 1 + \left( \dfrac{x + d/2}{L} \right)^2 \right]^{\frac{1}{2}} - L \left[ 1 + \left( \dfrac{x - d/2}{L} \right)^2 \right]^{\frac{1}{2}} \\ &= L \left[ 1 + \dfrac{\left(x + d/2 \right)^2}{2L^2} \right] - L \left[ 1 + \dfrac{\left(x - d/2 \right)^2}{2L^2} \right] \\ &= \dfrac{1}{2L} \cdot \left[ \left(x + d/2 \right)^2 - \left(x - d/2 \right)^2 \right] \\ &= \dfrac{1}{2L} \cdot 2xd \\ &= \dfrac{d}{L} x \end{aligned}$$

と表せます。

以下で計算の説明を簡単にします。

$S_1P$ の表式には三平方の定理を用いましょう。横方向が $L$, $x$ 方向が $x - \dfrac{d}{2}$ なので

$$S_1P = \sqrt{L^2 + \left( x - \dfrac{d}{2} \right)^2}$$

と表されます。

$S_2P$ の場合, $x$ 方向が $x + \dfrac{d}{2}$ になります。

また, 式変形の途中で以下の近似式を使用しています。

今回の場合, スリット間隔 $d$ は $\ell, L$ と比べて十分に小さい値なので

$$\left( \dfrac{x + d/2}{L} \right)^2 \ll 1$$

として良いのです。この近似式を用いて

$$L \left[ 1 + \left( \dfrac{x + d/2}{L} \right)^2 \right]^{\frac{1}{2}} \sim L \left[ 1 + \dfrac{\left(x + d/2 \right)^2}{2L^2} \right]$$

としています。

さて, 先の結果に戻ると経路差は

$$S_2P - S_1P = \dfrac{d}{L} x$$

と表せます。

この値から, ヤングの干渉実験における干渉条件は次のようにまとめられます。

ここからわかるように, 明線（暗線）の間隔は

$$\Delta x = \dfrac{L}{d} \lambda$$

です。明線の間隔と暗線の間隔は同じです。明線（暗線）の間隔はよく問われるので覚えておきましょう。

原点 $O \ (x=0)$ は必ず明線です。例えば演劇などの舞台で左右からのスポットライトが重なった時にさらに明るくなっている様子を思い出せば, とても納得しやすい結果ですね。

干渉縞の明線と暗線の位置は次のようになります。

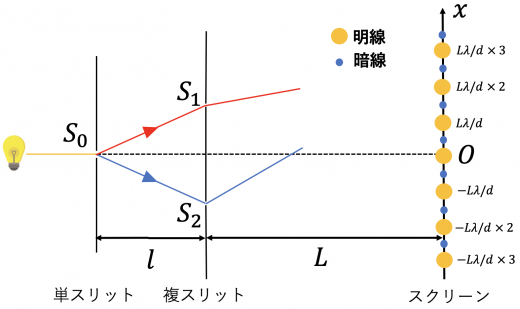
ただし, 中央の明線( $x=0$ )が一番明るく, $x$ 軸の中央から離れていくにつれて明線の明るさの強度は小さくなることも覚えておきましょう。

経路差については以下の図のように簡単に計算することもできます。ややトリッキーですが理解できると非常に簡単なので, この際に理解してしまいしょう。

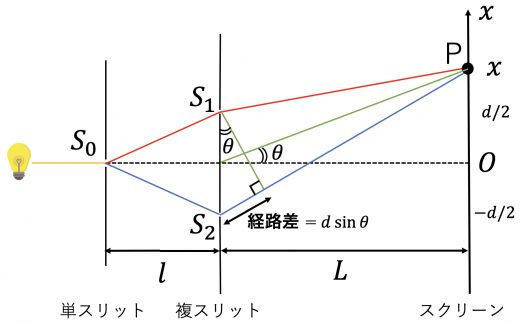
経路差は $d \sin \theta = d \tan \theta \sim d \dfrac{x}{L}$ と求められます。もちろんこの結果は先ほど近似式を使いながら長々と計算した時の結果と一致しています。

$\theta \ll 1$ の時, $\sin \theta \sim \tan \theta$ であるという近似も自在に使えるようにしておきましょう。

ヤングの実験で登場する近似式は他の分野でも役に立つことが多いのでしっかり覚えておきましょう。