位置エネルギーの定義と例（重力・弾性力・クーロン力）

空間の各点で，質点がその位置に来た時，それに作用する力が一義的に決まっている状況を考えます。そのようなとき，空間は力の場になっているといいます。力の場において，任意の経路 $C_{1},C_{2}$ に対し，$P_{0},P_{1}$ を始点，終点として， $$\int_{C_1 : P_{0} \to P_{1}}\boldsymbol{F}_{C}(\boldsymbol{r})\cdot d\boldsymbol{r}=\int_{C_2 : P_{0} \to P_{1}}\boldsymbol{F}_{C}(\boldsymbol{r})\cdot d\boldsymbol{r}$$ を満たす特別な力 $\boldsymbol{F}_C$ を保存力といいます。つまり，始点と終点さえ決めてしまえば，どんな経路を通って物体を運んでも，保存力のする仕事は変わらない という特別な力であるということです。ここで，この式は $$\int_{C_1 : P_{0} \to P_{1}}\boldsymbol{F}_{C}(\boldsymbol{r})\cdot d\boldsymbol{r} + \int_{-C_2 : P_{1} \to P_{0}}\boldsymbol{F}_{C}(\boldsymbol{r})\cdot d\boldsymbol{r} = 0$$ という式と同値です。ただし，$-C_2$ は $C_2$ を逆向きに進む経路を表します。$C_1,C_2$ は任意に経路をとっていますので，これは任意のループ $C$ を使って置き換えることができて， $$\oint_C \boldsymbol{F}_{C}(\boldsymbol{r})\cdot d\boldsymbol{r} = 0$$ と同値になります。 ここでストークスの定理：

を用いれば，$C$ が囲む図形を $S$ として， $$\oint_C \boldsymbol{F}_{C}(\boldsymbol{r})\cdot d\boldsymbol{r} = \int_S (\nabla \times \boldsymbol{F}_{C}(\boldsymbol{r})) \cdot \boldsymbol{n} dS = 0$$ $C$ つまり，$S$ は任意にとれるので， $$\nabla \times \boldsymbol{F}_{C}(\boldsymbol{r}) = \boldsymbol{0}$$ と同値になります。

つまり，$\nabla\times\boldsymbol{F}_{C}=\boldsymbol{0}$ は $\boldsymbol{F}_{C}$ が保存力であることの必要十分条件であることがわかります。

また，保存力の和は保存力であることは，定義から簡単にわかります。

位置エネルギー（ポテンシャルエネルギーと呼ぶこともあります）は，保存力に対して定義される物理量です。保存力 $\boldsymbol{F}_C(\boldsymbol{r})$ に対し，$\boldsymbol{r}_0$ を基準にした位置エネルギー $U$ を， $$U(\boldsymbol{r}) = - \int_{\boldsymbol{r}_0}^{\boldsymbol{r}} \boldsymbol{F}_C(\boldsymbol{r}) \cdot d\boldsymbol{r}$$ と定義します。保存力の定義により，この $U$ は $\boldsymbol{r}$ を決めれば一意に定まります。$U$ は $\boldsymbol{r}$ のみの関数です。この式から， $$\Delta U = U(\boldsymbol{r} + d\boldsymbol{r}) - U(\boldsymbol{r}) = -\boldsymbol{F}_C(\boldsymbol{r}) \cdot d\boldsymbol{r}$$ さて，全微分の式から， $$\Delta U = \dfrac{\partial U}{\partial x}dx+\dfrac{\partial U}{\partial y}dy+\dfrac{\partial U}{\partial z}dz=(\nabla U)\cdot d\boldsymbol{r}$$ とかけます。前2式において，$d\boldsymbol{r}$ は任意に取ることができますから， $$\boldsymbol{F}_C(\boldsymbol{r}) = -\nabla U$$ このように，保存力は位置エネルギーを使って簡潔に表すことができます。

仕事と運動エネルギーの関係の記事で， $$\Delta K = K(t_1) - K(t_0) = \int_{t_0}^{t_1}\boldsymbol{F}\cdot\boldsymbol{v}dt = \int_{\boldsymbol{r}(t_0)}^{\boldsymbol{r}(t_1)}\boldsymbol{F}\cdot d\boldsymbol{r}$$ が成立することを導きました。じつは，このうちの $\boldsymbol{F}$ を保存力と非保存力に分解すると，保存力の成分はエネルギーとして含めてしまうことができるのです。いかにその説明をします。

$\boldsymbol{F}$ を保存力の和 $\boldsymbol{F}_{\text{保}}$ と非保存力の和 $\boldsymbol{F}_{\text{非保}}$ に分解すると， $$\begin{aligned} K(t_1) - K(t_0) &= \int_{\boldsymbol{r}(t_0)}^{\boldsymbol{r}(t_1)}\boldsymbol{F}_{\text{保}}\cdot d\boldsymbol{r} + \int_{\boldsymbol{r}(t_0)}^{\boldsymbol{r}(t_1)}\boldsymbol{F}_{\text{非保}}\cdot d\boldsymbol{r}\\ &= \int_{\boldsymbol{r_0}}^{\boldsymbol{r}(t_1)}\boldsymbol{F}_{\text{保}}\cdot d\boldsymbol{r} - \int_{\boldsymbol{r_0}}^{\boldsymbol{r}(t_0)}\boldsymbol{F}_{\text{保}}\cdot d\boldsymbol{r} + \int_{\boldsymbol{r}(t_0)}^{\boldsymbol{r}(t_1)}\boldsymbol{F}_{\text{非保}}\cdot d\boldsymbol{r} \\ &= -U(t_1) + U(t_0) + \int_{\boldsymbol{r}(t_0)}^{\boldsymbol{r}(t_1)}\boldsymbol{F}_{\text{非保}}\cdot d\boldsymbol{r} \end{aligned}$$ $$\therefore \{K(t_1) + U(t_1)\} - \{K(t_0) + U(t_0)\} = \int_{\boldsymbol{r}(t_0)}^{\boldsymbol{r}(t_1)}\boldsymbol{F}_{\text{非保}}\cdot d\boldsymbol{r}$$ ここで，力学的エネルギー $E$ を $$E = K + U$$ つまり，運動エネルギーと全位置エネルギーの和として定義すれば， $$\Delta E = E(t_1) - E(t_0) = \int_{\boldsymbol{r}(t_0)}^{\boldsymbol{r}(t_1)}\boldsymbol{F}_{\text{非保}}\cdot d\boldsymbol{r}$$ と書くことができるのです。

ここから，「ある時間内で増加した分の力学的エネルギーは，非保存力のした仕事に等しい」ということができます。特に，「保存力のみが働く場においては，力学的エネルギーは一定である」ということもいうことができます。これを，力学的エネルギー保存の法則と呼びます。

重力などは，よく位置エネルギーで考えろと言われますが，その理由は上記のようなところにあったのです。保存力はエネルギーの項として含めることができる，それならば最初から運動エネルギーと混ぜて計算してしまえば，毎回仕事を求める必要がなくて楽じゃん！ という発想です。とても興味深い考察だと思います。

重力はベクトルで $$\boldsymbol{W} = \left(\begin{array}{c} 0\\ 0\\ -mg \end{array}\right)$$ と書くことができます。$z$ 軸は鉛直上向き方向としてとっています。計算するまでもなく， $$\nabla \times \boldsymbol{W} = \boldsymbol{0}$$ ですから，重力は保存力です。

保存力はどんな経路で線積分しても値がかわらないので，もっとも簡単な経路を取りましょう。

上図のような経路をとります。このとき， $$U = -\int_{z_0}^z \boldsymbol{W} \cdot d\boldsymbol{r}$$ です。$\boldsymbol{W}$ の $x,y$ 成分は $0$ であることから， $$\begin{aligned} U &= -\int_{z_0}^z (-mg) dz\\ &= \int_z^{z_0} mgdz\\ &= [mgz]_{z_0}^z\\ &= mg(z - z_0) \end{aligned}$$ と求めることができます。特に，$z_0 = 0$ のとき，$U = mgz$ となって，みなさんがよく知っている形の式になります。

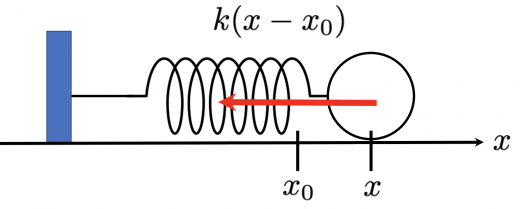
バネの自然長を $x_0$，バネ定数を $k$ とします。図のような状況の時，バネの弾性力は $-k(x-x_0)$ と表せます。右向きに $x$ 軸をとっています。ベクトルでは $$\boldsymbol{T} = \left(\begin{array}{c} -k(x-x_0)\\ 0\\ 0 \end{array}\right)$$ とかけます。これは少し計算すると，すぐに $$\nabla \times \boldsymbol{W} = \boldsymbol{0}$$ であることがわかるので，弾性力は保存力です。

これより， $$\begin{aligned} U &= -\int_{x_0}^x \left\{-k(x-x_0)\right\}dx\\ &= \left[\dfrac{1}{2}k(x-x_0)^2\right]_{x_0}^x\\ &= \dfrac{1}{2}k(x-x_0)^2 \end{aligned}$$ と求めることができます。

原点に電気量 $+q$ を持つ点電荷をおきます。このとき，単位電荷が受ける力は，クーロンの法則より， $$\boldsymbol{F} = kq\left(\begin{array}{c} \dfrac{x}{r^3}\\ \dfrac{y}{r^3}\\ \dfrac{z}{r^3} \end{array}\right)$$ とかくことができます。ここで，$r = \sqrt{x^2 + y^2 + z^2}$ です。つまり，$r$ も $x,y,z$ によることに注意する必要があります。このもと，$\nabla \times \boldsymbol{F}$ を計算することになるのですが，これは少し大変です。ぜひ練習としてやってみてください。

計算の末， $$\nabla \times \boldsymbol{F} = \boldsymbol{0}$$ であることがわかるので，クーロン力は保存力です。

さて，位置エネルギーを求めますが，基準点 $\boldsymbol{r}_0$ から $\boldsymbol{r}$ まで直線で結ぶと計算が大変になってしまいます。

そこで，上図のような経路 $C = C_1 + C_2$ をとることを考えてみます。

$C_1$ は原点を中心とする円弧上の運動です。つまりクーロン力とは直交する方向の移動です。よって，$C_1$ 上では $$\int_{C_1} \boldsymbol{F} \cdot d\boldsymbol{r} = 0$$ となります。よって，実質 $C_2$ の経路のみを考えればよいことになります。よって，$\boldsymbol{r}$ 方向の単位ベクトル $\boldsymbol{e}_r$ を用いて $$\begin{aligned} U &= -\int_{r_0}^r \boldsymbol{F} \cdot \boldsymbol{e}_r dr\\ &= -\int_{r_0}^r kq\left(\begin{array}{c} \dfrac{x}{r^3}\\ \dfrac{y}{r^3}\\ \dfrac{z}{r^3} \end{array}\right) \cdot \left(\begin{array}{c} \dfrac{x}{r}\\ \dfrac{y}{r}\\ \dfrac{z}{r} \end{array}\right) dr\\ &= -\int_{r_0}^r kq \dfrac{1}{r^2} dr\\ &= kq \left[\dfrac{1}{r}\right]_{r_0}^r\\ &= kq \left(\dfrac{1}{r} - \dfrac{1}{r_0}\right) \end{aligned}$$ 普通，クーロン力の位置エネルギーの基準点は $r_0 \to \infty$ にとることが多く，このとき， $$U = k\dfrac{q}{r}$$ となります。