作用反作用の法則〜ニュートンの第3法則〜

この法則においては2質点が主役として登場します。質点Aと質点Bがあったとして，AはBに $\boldsymbol{F}_{A\to B}$ という力を与えているとします。このとき，同時にBはAに $\boldsymbol{F}_{B\to A}$ という力を与えています。これは同時に起こります。作用に対して必ず反作用があります。2つの力は表裏一体，切っても切れない不可分の関係であるということです。 そして，これらには，次のような関係があります： $$\boldsymbol{F}_{A\to B} = -\boldsymbol{F}_{B\to A}$$ つまり，作用は反作用の逆ベクトル になっています。

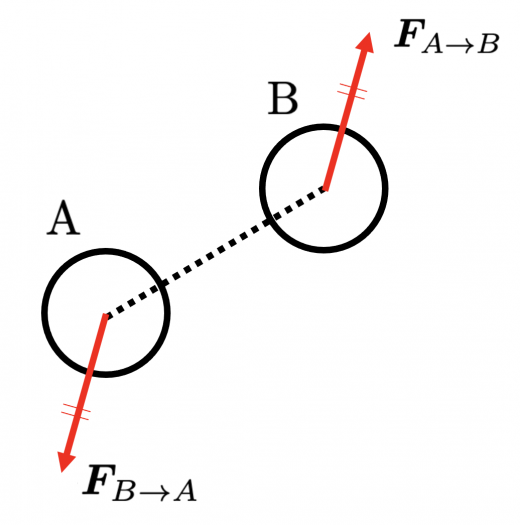
これはニュートンの3つの基本法則のうちの1つとして数えられるものです。「慣性の法則」や「運動方程式」同様，実験的にその正しさが認められているのであり，何か他のものから証明できる定理ではありません。

地面にボールが置いてあり，そのボールには重力が働いているとしましょう。

ボールに働く重力を「作用」だとした時，「反作用」は何でしょうか。

「垂直抗力」だと思った方，作用反作用の法則を理解した気になっていませんか？答えは，「地球がボールから受ける力」 です。なぜなら，重力は「ボールが地球から受ける力」だからです。

垂直抗力は「ボールが地面から受ける力」です。よって，その反作用は「地面がボールから受ける力」です。

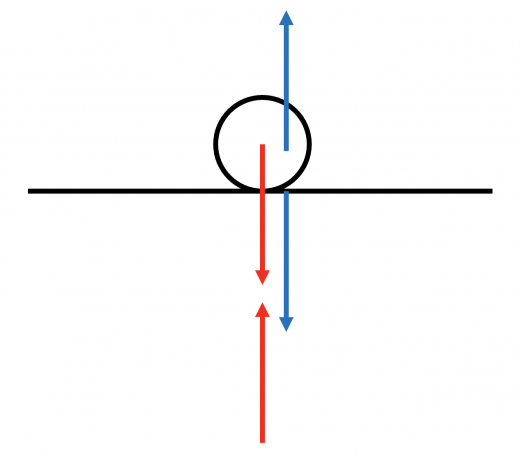
ボールに働く力は確かにつり合っていますが，つり合っている2力は別の物体からボールに働いている力です。「力のつりあい」と「作用反作用の法則」は初学者がよく混同してしまいます。慣れるまでは，この力はどの物体からどの物体に働いている力なのか？とよく考える癖をつけましょう。

慣性の法則，運動方程式は一つの質点に対して成立する重要な法則でした。作用反作用の法則は，複数の質点を統合的に考える際，とても重要な働きをします。

今，$n$ 個の質点があるとします。 質点同士が互いに与え合う力を「内力」，それ以外に外から与えられる力を「外力」と呼ぶことにします。

また，複数の質点をまとめて扱う際に，よく基準として使われる「重心」という概念があります。重心の位置ベクトル $\boldsymbol{\overline{r}}$ は，以下のように定義されます： $$\boldsymbol{\overline{r}} = \dfrac{\sum_{i=1}^n m_i \boldsymbol{r}_i}{\sum_{i=1}^n m_i}$$ ここで，$m_i, \boldsymbol{r}_i$ は $i$ 番目の質点の質量と位置ベクトルを表します。

例えば，同じ質量の2質点の重心は，ちょうど質点同士を結んだ線分の中点と一致します（重心の定義式から簡単にわかります）。重心は物体の「平均地点」のような役割をする点です。

さて，$i$ 番目の質点が与えられる外力を $\boldsymbol{F_i}$，別の $j (\neq i)$ 番目の質点から $i$ 番目の質点に与えられる内力を $\boldsymbol{F_{j \to i}}$ と書くことにすると，$i$ 番目の質点の運動方程式は $$m_i \dfrac{d^2 \boldsymbol{r_i}}{dt^2} = \boldsymbol{F_i} + \sum_{j\neq i}\boldsymbol{F_{j \to i}}$$ とかけます。ここで，$\sum_{j\neq i}$ は $j$ について $i$ 以外の値を全て動き，そのときの総和を取りなさい，という意味の記号として使っています。ここで，$\boldsymbol{F_{i \to i}} = \boldsymbol{0}$ と書くことにすれば， $$\sum_{i = 1}^{n} \sum_{j\neq i}\boldsymbol{F_{j \to i}} = \sum_{i = 1}^{n}\sum_{j = 1}^n\boldsymbol{F_{j \to i}} = \dfrac{1}{2} \sum_{i = 1}^{n}\sum_{j = 1}^{n}(\boldsymbol{F_{i \to j}} + \boldsymbol{F_{j \to i}})$$ ここで，作用反作用の法則： $$\boldsymbol{F_{i \to j}} + \boldsymbol{F_{j \to i}} = \boldsymbol{0}$$ が効いてきます。これを用いると，内力に関する項は作用反作用の法則により，総和をとると $\boldsymbol{0}$ になってしまうのです。よって，質点 $n$ 個分の運動方程式を全て足し合わせると，次のようになります： $$\sum_{i = 1}^{n}\left(m_i \dfrac{d^2 \boldsymbol{r_i}}{dt^2}\right) = \sum_{i = 1}^{n}\boldsymbol{F_i}$$ $M$ を $n$ 個の質点の質量の総和のことだとすると， $$\therefore M \dfrac{d^2 \boldsymbol{\overline{r}}}{dt^2} = \sum_{i = 1}^{n}\boldsymbol{F_i}$$ とかくことができてしまいます。つまり，質点系の重心は，その点に系の全質量と全外力が集中した1個の質点と同じ運動を行うということです。$n$ 個の質点をばらばらに解析しなくとも，系の中心を簡単に記述することができるのです。

このように，作用反作用の法則は，系の内部で働く内力に対して総和を取る時に，とても重要な働きをします。