力のつりあい・作用反作用との違い
この記事では,力のつりあいとは何であるか,また力のつりあいと作用反作用の法則との違いを詳しく解説します。
力のつりあい
力のつりあい
1つの物体に複数の力が働いており,その合力が であるとき,力がつりあっている状態であると言います。合力の定義については→ベクトルとしての力の合成・分解の記事を参考にしてください。図で表すならば,以下のような状態です。

力の合成とつりあい
よく「同一直線上にある」ことが力のつりあいの条件としてあげられますが,大きさがない質点のような物体に対してはその条件は必要ありません。以下の図のように,1つの物体に3つの力がかかっている状況を考えてみましょう。

右2つのななめの力の合力は,次の図の赤い矢印のようになります。

赤と青の合力が になるなら,3力は(一直線上にあるわけではないが)つり合っていると言えます。
ちなみに,大きさを持つ物体に対しては「同一直線上にある」という条件が効いてきます。これは「力のモーメント」というものにかかわる話であり,別の記事で解説します。
力の分解とつりあい
以下のような3力がかかっている状況を考えます。

力のつりあいの条件は であることでした。このままでは合力が になっているのかどうかわかりづらいです。先ほどは力の合成により3力のつりあいを考えましたが,ここでは見方を変え,「力の分解」をすることを考えてみます。
今は平面上の力を考えていますから, 方向, 方向ともに合力の成分が になればよいです。つまり,あえて書けば,合力が となればよいです。赤い矢印で表された力を分解すると,
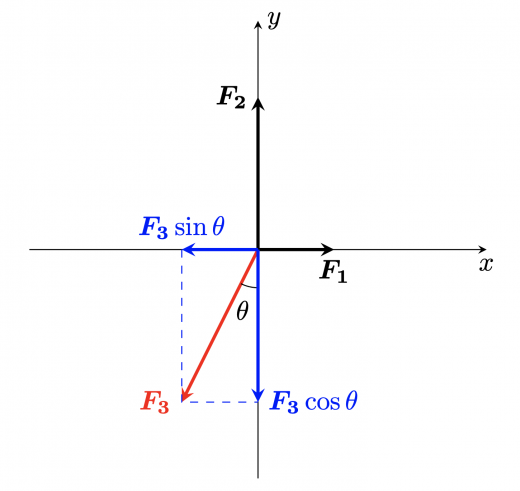
方向を正とした 軸方向の合力は, 方向を正とした 軸方向の合力は, よって,つりあいの条件は とかけます。
作用・反作用の法則との違い
作用・反作用の法則との違い
初学者の方の中には,「力のつりあい」と「作用反作用の法則〜ニュートンの第3法則〜」を混同してしまう方が多くいます。しかし,これらは全く異なった概念です。これらの違いについて詳しく解説してみます。
作用反作用の法則とは, 「物体Aがある物体Bに力を作用させたとき,Bから,大きさが等しく逆向きの反作用をAが受ける」 という法則のことを言います。力を作用させるとは,「力を加える」ということです。
ちなみに,これはニュートンの三法則の一つとして数えられる原理であり,どうしてこれが成立するのか?などと考える余地のあるものではありません。
作用反作用の法則では,A,Bという2つの物体がダブル主役として登場していることに注意しましょう。
これに対し,力のつりあいとは,1つの物体にかかる力の合力を考えています。力のつりあいにおいては1つの物体がソロで主人公をつとめているのです。
力のつりあいと作用反作用の法則は全く別のことを言っていることが理解されたと思います。











