仕事と運動エネルギーの関係

仕事と呼ばれる量は，物理では以下のように定義されます：

$\boldsymbol{F} \cdot \Delta\boldsymbol{r}$ は，力と変位ベクトルの内積です。つまり，仕事 $\Delta W$ はスカラー量になります。

例をみてみましょう。

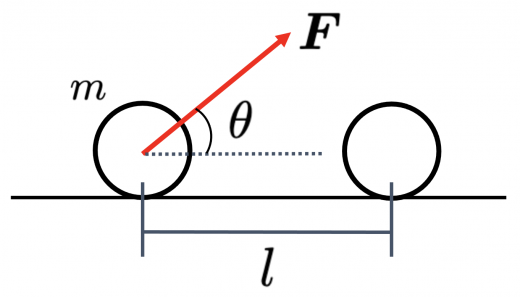
物体に，一定の力 $\boldsymbol{F}$ を図のような方向に加えます。この状態で，物体を水平方向に $l$ だけ動かします。図の右方向の単位ベクトルを $\boldsymbol{e}_x$ で表すことにします。この間，力 $\boldsymbol{F}$ は以下の大きさの仕事をします： $$\begin{aligned} \Delta W &= \boldsymbol{F} \cdot l \boldsymbol{e}_x\\ &= \|\boldsymbol{F}\| l \cos \theta \end{aligned}$$

ただ単に，力を加えていても，力を加えている対象が全く動かなければ仕事は発生しない ということに注意してください。

仕事には運動エネルギーと密接な関係があることを以下で説明していきます。

運動エネルギーと呼ばれる量は，物理では以下のように定義されます：

なぜ $\dfrac{1}{2}$ が付くのか，$\|\boldsymbol{v}\|$ の2乗が入るのかなど疑問は残りますが，これは定義ですので議論の余地はありません。こう定義すると仕事との関係がうまく説明できるから，という理由だけです。

では，仕事とエネルギーの関係について議論します。質点の運動方程式： $$m \dfrac{d{\boldsymbol{v}}}{d{t}} = \boldsymbol{F}$$ からはじめます。

運動方程式の両辺で，$\boldsymbol{v}$ と内積をとると， $$\boldsymbol{v} \cdot m\dfrac{d{\boldsymbol{v}}}{d{t}} = \dfrac{m}{2} \dfrac{d}{dt}\left(\boldsymbol{v}\cdot\boldsymbol{v}\right) = \dfrac{d}{dt}\left(\dfrac{1}{2}mv^2\right) = \boldsymbol{F}\cdot\boldsymbol{v}$$ と書き換えられます。ここで， $$\dfrac{d}{dt}\left(\boldsymbol{v}\cdot\boldsymbol{v}\right) = \dfrac{d{\boldsymbol{v}}}{d{t}}\cdot \boldsymbol{v} + \boldsymbol{v}\cdot\dfrac{d{\boldsymbol{v}}}{d{t}} = 2 \boldsymbol{v}\cdot\dfrac{d{\boldsymbol{v}}}{d{t}}$$ を利用しています。$t_0$ から $t_1$ の間で積分すれば， $$\Delta K = K(t_1) - K(t_0) = \int_{t_0}^{t_1}\boldsymbol{F}\cdot\boldsymbol{v}dt = \int_{\boldsymbol{r}(t_0)}^{\boldsymbol{r}(t_1)}\boldsymbol{F}\cdot d\boldsymbol{r}$$ この式より，「ある時間内で増加した分の運動エネルギーは，仕事に等しい」と言うことができます。これが，仕事とエネルギーの関係の式です。

この式からわかることは，仕事とエネルギーの変動は完全に対応するということです。仕事とエネルギーは表裏一体なのです。

特に，仕事が0，つまり $\int_{\boldsymbol{r}(t_0)}^{\boldsymbol{r}(t_1)}\boldsymbol{F}\cdot d\boldsymbol{r} = 0$ の場合， $$\Delta K = 0$$ つまり， $$K = \mathrm{const.}$$ となります。これをエネルギー保存の法則と呼びます。

せっかくですので1問例題を考えてみましょう。

仕事とエネルギーの関係式により， $$\begin{aligned} \dfrac{1}{2}mv^2 - \dfrac{1}{2}mv_0^2 &= \int_{t_0}^{t_1} (mg) \cdot vdt\\ &= \left[mgx\right]^H_h\\ &= mg(H-h) \end{aligned}$$ これを $v$ について整理すれば， $$v = \sqrt{2g(H-h) + v_0^2}$$ と求めることができます。