単振動のまとめ

復元力は，以下のように定義されます：

復元力の大きさは，現在の位置 $x$ と $x_C$ がどれくらい離れているか，その絶対距離に比例しています。例えば，$x$ が $x_C$ から正の方向に離れれば離れるほど，$F$ はどんどんマイナス側の小さい値になっていきます（符号はマイナスで，絶対値がどんどん大きくなるということです）。逆に，$x$ が $x_C$ から負の方向に離れていくと，$F$ はどんどん大きい値になります。

つまり，$F$ は $x$ を $x_C$ の方向に戻そうとする向きに働く力であるということです。 この意味で $F$ は「復元」力と呼ばれています。

質量が $m$ であって，中心が $x_C$ の復元力が働いているような質点の運動を考えます。運動方程式を立式すると $$m \ddot{x} = - K (x - x_C)$$ $$\therefore \ddot{x} = - \dfrac{K}{m} (x - x_C)$$ とかけます。$\dfrac{K}{m}$ は正の値ですから，これを $\omega^2$ とおきかえることができて， $$\ddot{x} = - \omega^2 (x - x_C)$$ と書くことができます。これは二階線形微分方程式と呼ばれ，この微分方程式は数学的に厳密に解くことができます。その一般解は， $$\begin{aligned} x(t) - x_C &= a \sin (\omega t + \alpha)\\ &= a \cos (\omega t + \beta)\\ &= A \cos \omega t + B \sin \omega t \end{aligned}$$ で表されることが大学等の数学を学ぶと証明できます。ここで，$a,\alpha,\beta, A,B$ は「任意定数」と呼ばれる定数です。 数学において，不定積分を計算する際，積分定数というものをつけると思いますが，あれは積分後の結果に定数分の猶予，自由があるということを表していました。それと同様に，$a,\alpha,\beta, A,B$ は一般解に猶予を持たせるためのものです。初期条件などが与えられれば，これらは一意に決定することができるようになります。

微分方程式の一般解とは，一般解が微分方程式の解であることを保証するだけではなく，この微分方程式の解になるものは一般解の形のもので尽くされており，他にこの一般解の形を逸脱した解は存在しないということも主張しています。つまり，

であるということです。

先ほども言及したように，この式の左から右，つまり微分方程式を解く，という計算は高校数学の範囲を超えてしまいます。ただ，右から左，つまりこの解が微分方程式を満たすということは簡単に証明することができます。証明は以下の通りです： $$\begin{aligned} \dfrac{d}{dt} (x(t) - x_C) &= a\omega \cos (\omega t + \alpha)\\ \dot{x} &= a\omega \cos (\omega t + \alpha)\\ \therefore \ddot{x} &= -a\omega^2 \sin (\omega t + \alpha)\\ &= -\omega^2 (x(t) - x_C) \end{aligned}$$

物理量 $x(t)$ が単振動をするということがわかったなら，これは $$x(t) = a \sin (\omega t + \alpha) + x_C$$ と表されることが確定します。単振動はもうすでに一般解がもとまってしまっている運動であり，（計算が複雑になることはあれど）とても簡単な運動であるということです。単振動に苦手意識を持っている方も少なくないと思いますが，困ったら一般解を書き出してしまえば済んでしまうのです。そんなに単振動に対して身構える必要はありません。

物理量が $t$ で一般的に表されてしまっているので，速度，加速度も簡単に導くことができます。ただ微分するだけですね。先ほど，一般解が微分方程式を満たすことを証明したときの数式の中に，すでに答えが紛れ込んでいました。速度は， $$\dot{x} = a\omega \cos (\omega t + \alpha)$$ 加速度は， $$\ddot{x} = -a\omega^2 \sin (\omega t + \alpha)$$ で表されます。

さて，下図のような等速円運動を考えてみましょう。

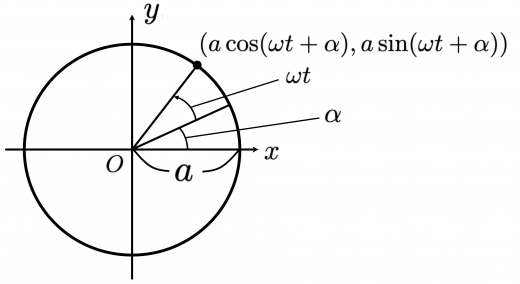
半径 $a$ 上，初期角度 $\alpha$，角速度 $\omega$ で等速円運動している物体の位置は， $$\left(a\cos (\omega t + \alpha), a\sin (\omega t + \alpha)\right)$$ で表されます。

では，図の左側から光をあて，右にある壁に投影してみましょう。すると，壁にできた像は $$y = a\sin (\omega t + \alpha)$$ という1次元の運動をします。これはまさに単振動になっています。つまり，「等速円運動している物体の正射影は，単振動をする」 ということが言えます。

単振動を特徴づけるいくつかの物理量を紹介します。

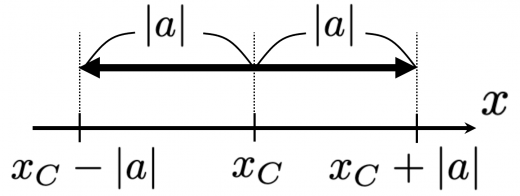
$x(t) = a \sin (\omega t + \alpha) + x_C$ なる単振動において，

• 周期 $T$ ：1回振動するのに要する時間。
• 角振動数 $\omega$ ：単位時間あたりの位相変化。
• 振動数 $f$ ：単位時間あたりの振動回数。
• 振幅 $|a|$ ：名前の通り単振動の振幅。

これらは問題でもよく求めることを要求されることになります。よく理解しておきましょう。

単振動の分野では，よくグラフについても議論を要求されることがあります。例をみておきましょう。

$x(t) = A \sin \omega t$ で表される単振動を考えます。この速度は， $$\dot{x} (t) = A\omega \cos \omega t$$ で表されます。これらのグラフを描くと，以下のようになります。

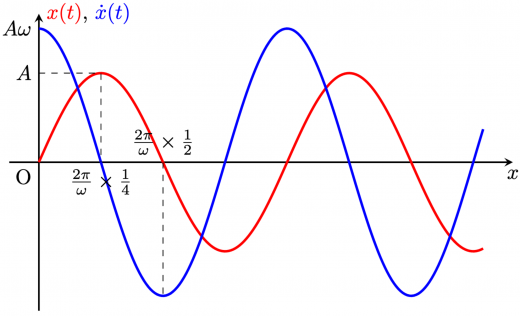
グラフを見ればわかる通り，$x(t), \dot{x}(t)$ において，どちらかが $0$ のとき，もう一方は絶対値が最大になっています。これは，数式を見れば理由が明らかです。$x(t), \dot{x}(t)$ のペアは，位相が同じな $\sin,\cos$ のペアになっています。$\sin,\cos$ は，どちらかが $0$ のとき，もう一方は絶対値が最大，つまり $1$ になっています。例えば，$\sin \theta , \cos \theta$ において，$\theta = \dfrac{\pi}{2}$ のとき，$\sin \theta = 1, \cos \theta = 0$ ですし，$\theta = \pi$ のとき，$\sin \theta = 0, \cos \theta = -1$ です。

速度と加速度のグラフのペアについても，上記と同様なことが言えます。

グラフをかくと，数式だけを睨むより，理解が早く進むことがあります。詰まってしまったときは，グラフを書いてみることをおすすめします。

単振動を作り出す復元力は，バネの弾性力と全く同じ形をしています。位置エネルギーの定義と例（重力・弾性力・クーロン力）の記事の「弾性力による位置エネルギーの公式」という節と同様の議論をすれば，単振動のエネルギーを簡単に求めることができて

となります。

この公式は，速さの最大値を求める問題などで活躍します。一般解をもとめてから計算するよりも，はるかにこの公式を使う方がはやいことが多いです。意外と忘れられがちな式ですが，重要な式です。使い方の例についてはまた別の記事で紹介したいと思います。